Pour que Bramah tombe

(Article essentiellement destiné à ceux qui ont toujours eu du mal avec la récurrence, et aux autres)

Au commencement des temps, Dieu créa, dans le temple de Benares, sous le dôme qui marque le centre du monde, la Tour de Bramah, composée de 3 aiguilles de diamant, sur lesquels repose une pyramide de 64 disques en or pur de tailles différentes, posées les uns sur les autre. Il ordonna aux prêtres de déplacer  jours et nuits les disque de la première aiguille à la troisième, sans jamais toucher plus d'un seul disque à la fois, ni poser un disque sur un disque de plus petite taille. Quand les prêtres auront terminé leur tâche, la tour s'écroulera, et le monde arrivera à sa fin. (D'après Edouard Lucas)

La tour de Hanoï

Plus proche de nous, il y a la tour de Hanoï, inventé par Lucas en 1883, qui consiste en une tour de 8 disques empilés les uns sur les autres par ordre de tailles décroissantes sur un axe vertical. Le but du jeu est de transferer ces 8 disques sur un autre axe vertical, un troisième étant disponible, sans poser de disque sur un disque plus petit, et sans prendre plus d'un disque à la fois.

A gauche, l'illustration originale de Lucas.
1 : Position initiale des 3 axes.
2 : Position intermédiaire
3 : Position finale

Vous pouvez vous essayer au jeu avec cet applet.

La question nous brûle à présent, c'est : quand aura lieu la fin du monde ?
Posée autrement, la question est : si une tour de Hanoï est composée de n disques, combien de déplacement au minimum seront nécessaires pour déplacer la tour ?

Le maitre-mot pour répondre à cette question est "récurrence" ! Même si ce mot peut parfois faire peur, n'oublions pas que la récurrence est notre amie.

Combien pour cette tour de Hanoï ?
Appelons pour la suite T_n le nombre minimal de déplacement nécessaire pour bouger une tour de Hanoï de taille n d'un axe à un autre.

Procédons par tâtonnements :
Si la tour n'est composée d'aucun disque, il nous faudra aucun mouvement pour la déplacer. Donc T₀=0.
Si la tour est composée d'un seul disque, il nous faudra un coup au minimum pour la déplacer. Donc T₁=1.

On a T₀, on a T₁. Il est donc temps de généraliser à n'importe quel n ! Passons donc à T_n.

Une stratégie possible pour déplacer une tour de taille n, c'est de d'abord déplacer les n-1 plus petits disques sur le deuxième axe, de déplacer le plus grand des disques sur le troisième axe, puis de déplacer la tour du deuxième axe sur le grand disque, sur l'axe 3..

Dans le cas n=2, par exemple : on déplace le petit disque sur l'axe 2 (1 coup), on déplace le grand disque sur l'axe 3 (2 coups) puis on déplace le petit disque sur l'axe 3 (3 coups). Donc T₂≤3 ! (On met le signe ≤ car on n'est pas encore certains qu'il n'y a pas une solution plus rapide)

Dans le cas n=3 : on déplace les deux plus petits disques sur l'axe 2 (3 coups), on déplace le grand disque sur l'axe 3 (4 coups) puis on déplace les deux disques de l'axe 2 sur l'axe 3 (7 coups). Donc T₃≤7.

Dans le cas général, avec notre stratégie : on déplace les n-1 plus petits disques sur l'axe 2 (T_n-1 coups), on déplace le grand disque sur l'axe 3 (T_n-1 +1 coups) puis on déplace les n-1 plus petits disques sur l'axe 3 (2.T_n-1+1 coups).

On a alors la formule générale : T_n≤2.T_n-1 +1 (Formule qui permet de majorer le nombre minimal de coup)

Est-il possible de le faire en moins de coups ? Et bien, malheureusement, non ! En effet, il faut à un moment ou à un autre déplacer le plus grand des disques, et on ne peut le déplacer que si tous les disques sont bien rangés en position centrale (sinon, il faudrait mettre le grand disque sur un plus petit). Il faudra donc T_n-1 déplacements pour mettre les n-1 plus petits disques au milieu, 1 déplacement de plus pour déplacer le grand disque, et redéplacer la tour centrale sur le grand disque en T_n-1 déplacements. Moralité : Le nombre minimal de mouvement T_n est plus grand que 2.T_n-1 +1.
On en conclut :

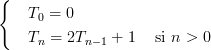
Cette relation permet de calculer T_n seulement si on connaît la valeur de T_n+1. Puisque l'on connaît T₀, on peut calculer n'importe quel T_n. Une formule de ce genre est appelée "relation de récurrence".

Combien, pour cette tour de Bramah ?
Pour connaitre le nombre de mouvements nécessaires aux prêtres pour bouger la Tour de Bramah, il ne reste plus qu'à calculer T₆₄ !
T₀ = 0
T₁ = 2×0 + 1 = 1
T₂ = 2×1 + 1 = 3
T₃ = 2×3 + 1 = 7
T₄ = 2×7 + 1 = 15
T₅ = 2×15 + 1 = 31
T₆ = 2×31 + 1 = 63
T₇ = 2×63 + 1 = 127
T₈ = 2×127 + 1 = 255 (Il faut 255 coups pour déplacer la tour de Hanoï originale !)

Rendu à T₈, je fatigue déjà... N'y aurai t'il pas un moyen plus rapide pour trouver T₆₄ ? Une formule qui donnera la solution en fonction de n, par exemple, et pas en fonction de T_n-1 ?
En regardant les résultat que l'on a, on peut très facilement supposer que T_n=2ⁿ-1 ! (Sauf erreurs de calcul de ma part, le résultat est vrai pour n ≤ 8.)

Mais comment peut on démontrer cette formule ?... "Récurrence" !
On sait que la formule générale est vraie pour n ≤ 8. Peut-on changer ça en n ≤ 9 ? Et en n ≤ n'importe quel nombre ?
Supposons que pour l'entier p, on a T_p=2^p-1. (Ici, p=8). Alors,
T_p+1 = 2.T_p+1  (C'est la formule de récurrence)
   = 2.(2^p-1)+1   (On a supposé que T_p=2^p-1)
   = 2.2^p -2 + 1
   = 2^p+1 - 1

Donc, la formule est vraie pour n=p+1 ! Si la formule est vraie pour n=8, elle est vraie pour n=9, et donc vraie pour n=10, et donc, vraie pour n'importe quel n !

Et donc, pour n=64, on trouve T₆₄ = 18 446 744 073 709 551 615. A raison de 1 déplacement par secondes, cela fera... 5 milliards de siècles, c'est à dire, 5 000

Epatez vos amis !

Et dans la pratique, comment faire pour déplacer une tour de Hanoï en un temps record ? Voici la solution à mettre en place dès que le chemin de votre vie ce genre de tours.
Main droite sur le plus petit des anneaux, main gauche libre. Un déplacement sur 2 consistera à déplacer le petit anneau, toujours dans le même sens. L'autre déplacement, ça sera effectuer le seul autre mouvement possible.

Voici un petit exemple, trouvé au hasard sur Dailymotion :

En donnant un nom aux anneaux, du plus petit au plus grand (1,2, 3, ...), on peut résumer les déplacements à effectuer par l'anneau à bouger. Cela va donner :
C₁ = 1
C₂ = 1, 2, 1
C₃ = 1, 2, 1, 3, 1, 2, 1
C₄  = 1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2, 1
C_n = C_n-1, n, C_n-1

Maintenant, prenez une bande de papier, et pliez la en deux.
Notez la pliure par '4', puis pliez la à nouveau.
Notez les 2 nouvelles pliures par '3', puis pliez la à nouveau.
Notez les nouvelles pliures par '2', puis pliez la à nouveau.
Notez les nouvelles pliures par '1', puis dépliez tout...

On retrouve C₄ ! Épatant non ?...

---

Sources :
Récréations mathématiques édition III, Edouard Lucas (Pour l'illustration du haut)

Comments

[Rocky]

On peut aussi remarquer que le premier anneau se deplace tous les 2 coups (2^1) dans un sens, le deuxieme anneau tous les 4 coups (2^2) dans l'autre sens, le troisieme tous les 8 coups (2^3) dans le meme sens que le premier, etc...

On peut donc prevoir que l'anneau n se déplacera qu'une seule fois, et donc on arrive facilement a 2^n-1 ...