Petit déjeuner au lit
Samedi 14 février, Saint-Valentin : s'il y a bien un jour où il faut amener le petit déjeuner au lit à votre coquelicot d'amour, c'est bien celui-là (Mais si, la fête des amoureux, tout ça) ! Un croissant qui sort de la boulangerie, un grand verre de jus d'orange maison, un panier de fruits frais et une tasse vide, attendant son contenu en café, encore au chaud dans la cafetière.
- Ma chérie, regarde le fond de la tasse sous les rayons du Soleil !
- Quoi donc ?... Oh ! Mon amour, il y a un cœur !
- Oui, je l'ai mis pour toi, ma petite perle des mers du sud !

Quelle belle caustique de cercle !
La courbe simple qui s'approche le plus du cœur, pour un matheux, c'est la cardioïde (Du grec "kardia" ("cœur"), baptisé en 1741 par Castillon). C'est la courbe que décrit un point sur un cercle roulant sur un autre de même taille (C'est donc une épicycloïde, courbe obtenue en faisant rouler un cercle sur un autre):
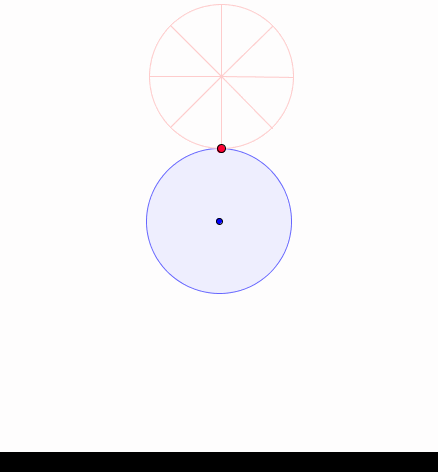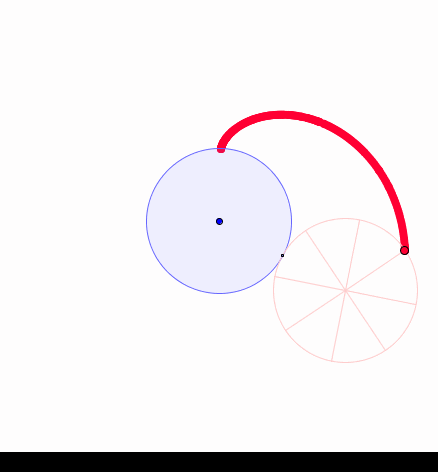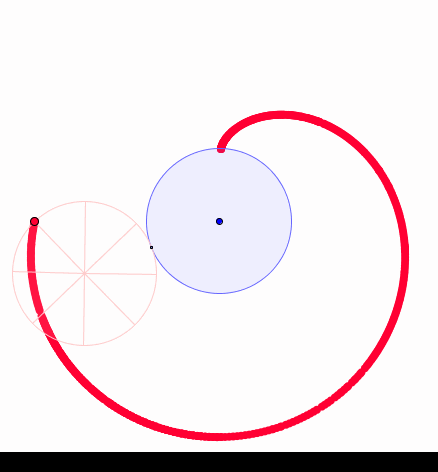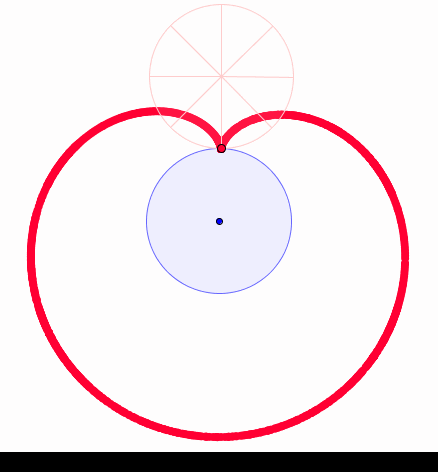
Construction d'une cardioïde
Reste la question... Qu'est ce qu'une cardioïde vient faire au fond de ma tasse de café ?!
La réponse nous est apportée par une petite étude des rayons lumineux arrivant sur la tasse. Notre tasse, c'est un cercle, et les rayons lumineux provenant du Soleil, on peut supposer qu'ils sont tous parallèles. Un rayon (ici, en bleu) cognera sur la tasse (en I) et sera alors réfléchi (en rouge) en formant un angle égal à celui d'incidence :
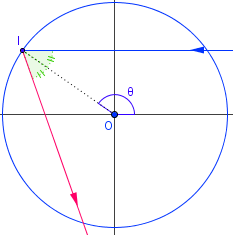
Réflexion d'un rayon
Ca, c'est pour un seul rayon provenant du Soleil. Quand on en met un peu plus, on remarque que les rayons se focalisent le long d'une courbe...

Quelque chose se dessine...
{Attention, la partie qui arrive est remplie d'équations, en cas d'allergie, il est conseillé de la sauter}
Mais sur quelle courbe se focalisent exactement ces rayons ? La courbe qui se dessine, c'est "l'enveloppe " des rayons, c'est à dire, la courbe dont les tangentes sont ces rayons. Cette enveloppe, on peut la calculer explicitement, en cherchant la la courbe Γ telle que tous les rayons soient tangents à Γ.
Cherchons déjà quelle est la famille de droites (de rayons réfléchis) à considérer. On peut paramétrer l'équation du rayon réfléchi par l'angle θ, tel que représenté dans le schéma un peu plus haut. L'équation du rayon est alors :
D(θ) : sin(2θ).x - cos(2θ).y = sin(θ)
On a alors une famille (D(θ)) de droites, et il faut retrouver la courbe Γ, de paramétrage M(θ)=(x(θ),y(θ)) telle que, pour tout t, on a M(θ)∈D(θ) et ![]() . Autrement dit, M(t)=(x(θ),y(θ)) vérifie :
. Autrement dit, M(t)=(x(θ),y(θ)) vérifie :
![]()
En dérivant la première égalité, on trouve :
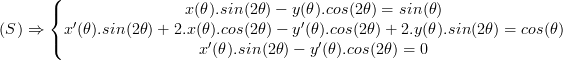
Et en soustrayant la troisième ligne à la deuxième, on trouve le système suivant :
![]()
que l'on peut résoudre en :
![]()
On trouve alors l'équation paramétrée de la courbe Γ.
{Fin de zone dangereuse}
Les calculs sont formels : les rayons se focalisent sur la courbe Γ définie juste au dessus. Avec un logiciel traceur, on peut voir la tête de la courbe, qui est...
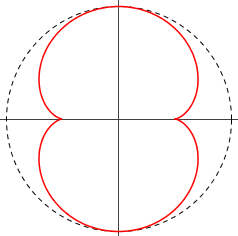
Oh, la belle néphroïde !
... qui est, non pas une cardioïde, mais une néphroïde (On peut avoir l'impression de voir une cardioïde dans la tasse, puisque seule une moitié est visible, mais ce n'est qu'une demi-néphroïde) ! Du grec "néphros", comme rein, c'est également une épicycloïde, puisqu'elle peut-être obtenue en faisant rouler un cercle sur un cercle de rayon double :

La néphroïde est une épicycloïde. Si si.
Contrairement à la cardioïde, la néphroïde n'a absolument rien de romantique... Aucune inquiétude à avoir, cet évènement fâcheux ne viendra pas gâcher votre Saint-Valentin, puisqu'on peut faire apparaitre miraculeusement un cœur dans la tasse ! Il faut simplement changer la source lumineuse.
En provenant du Soleil, les rayons arrivent parallèles et forment une néphroïde. Si la source lumineuse est placée sur le bord de la tasse, les rayons ne seront plus parallèles, et les choses seront différentes :

Mais... Ca m'a l'air d'être une cardioïde !
{Histoire de refaire rapidement des calculs, on peut voir que l'équation du rayon réfléchi est:
D(θ) : (sin 2θ -sin θ).x + (cos θ - cos 2θ).y=sin θ
Et le calcul de l'enveloppe de la famille (D(θ)) permet de trouver (après de fastidieux calculs) :
![]()
}
La courbe une fois tracée est la suivante :

Oh, la belle cardioïde !
Cette fois-ci, on retrouve bien une cardioïde au fond de notre tasse !... La Saint-Valentin est sauvée !
Sources :
La courbe du petit déjeuner - Tangente n°125, Novembre-Décembre 2008
Photos : là



/http%3A%2F%2Fstorage.canalblog.com%2F68%2F79%2F210892%2F119772528_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F43%2F63%2F210892%2F119161093_o.gif)
/http%3A%2F%2Fstorage.canalblog.com%2F74%2F79%2F210892%2F116430959_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F50%2F97%2F210892%2F91694671_o.png)