Jeu, set et match
Roger Federer est-il le meilleur joueur du monde ? La réponse dans cet article remplie de jolies équations, et de charmants graphiques ! Après le sport le plus aléatoire de la semaine dernière, passons à celui le plus prévisible : le tennis !
Rappelons-en rapidement les règle.
Le principe de base de ce sport est de taper dans une baballe à l'aide d'une raquette. En face de soi, l'adversaire doit faire de même, l'idée globale étant d'empêcher son adversaire de rattraper cette dite baballe. Si votre adversaire ne la rattrape pas ou la renvoie dans une zone du jeu inadaptée, vous marquez une quinzaine de point. En marquant des points, on gagne des jeux ; en gagnant des jeux, on gagne des set ; en gagnant des sets, on remporte le match.
Soyons plus précis : pour remporter un jeu, il faut gagner au moins quatre points, avec une avance de deux points (au détail près que le décompte des points se fait sous la forme 0-15-30-40-JEU, un système irrationnel hérité du jeu de paume). Pour remporter un set "sans tie-break", il faut gagner au moins 6 jeux, avec deux points d'écart. Dans un set "avec tie-break", les mêmes règles s'appliquent, mais si le score en vient à être 6/6, un jeu décisif se joue (le premier rendu à au moins 7, avec deux points d'écarts), et qui gagne gagne. Un match se joue en 5 sets (4 sets "avec tie-break" + 1 "sans tie-break"), il faut en remporter (au moins) 3 sur 5 pour gagner le match.
Maintenant que l'on a tous bien compris le décompte des points, il est temps de se poser la question qui fâche : imaginons que je dispute un match contre Federer. Sachant que j'ai à peu près une chance sur 3 de réussirun point, quelle est ma probabilité de gagner un match contre lui ?
Étape un : gagner un jeu
Pour gagner un jeu contre Federer, le plus simple est de gagner 4 points successifs : la probabilité est de p4, où p=1/3 est ma probabilité de gagner un point (La probabilité est donc d'une chance sur 81 : c'est faisable). A moins que je lui laisse gagner un point sur 5, ce qui peut se passer de 4 manière différente : il gagne le 1er coup et je gagne les 4 autres, il gagne le 2eme et je gagne les 4 autres etc. En notant q sa probabilité de gagner (et donc, q=1-p), ma probabilité de gagner de cette façon est de 4qp4. On peut voir les choses par ce tableau, où un jeu gagnant est un chemin dans le tableau partant de 0-0 et arrivant dans une case bleue.

Combinatoire d'un jeu
Les nombres dans les cases indiquent le nombre de façon d'accéder à un score donné. En bleu les issues favorables, en jaune les défavorables, en gris les égalités (40-A).
On peut voir par exemple qu'il y a 10 façons de gagner avec un score final de 4-2, 20 avec 5-3, etc.
La probabilité pour moi de gagner un jeu est donc :
p4+4qp4+10q2p4+20q3p5+40q3p5+80q4p6+...
A cause de cette règle des deux points d'écart, un jeu peut durer théoriquement aussi longtemps que l'on veut (en oubliant la pluie, la nuit...), d'où la somme infinie. Les observateurs auront remarqué qu'il s'agit en fait d'une somme géométrique, et auront simplifié d'eux mêmes : la probabilité de gagner un jeu est donc de :
![]()
Ce qui, en graphique, donne :

Probabilité de gagner un jeu en fonction de la probabilité de marquer un point.
A la vue de la courbe, on peut dire que le système des points amplifie la domination du plus fort : si j'ai une chance sur 3 de gagner un point, j'aurais une probabilité de gagner un jeu de 35/243 ! (Environ 1/7).
Étape deux : gagner un set
Maintenant que l'on sait comment gagner un jeu, il est temps de gagner un set ! Un set peut se gagner avec un score de 6/0, 6/1, 6/2, 6/3, 6/4 ou 7/6. Si c'est 6/6, c'est tie-break, et on rigole (pour les calculs...).
Dans le cas d'un set sans tie-break, les choses sont similaires au cas précédent.
On peut résumer les choses avec ce tableau :
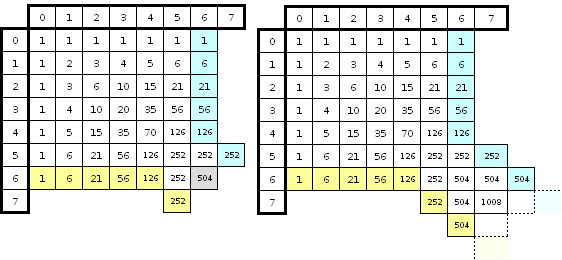
Combinatoire d'un set (à gauche, avec tie-break [en gris] ; à gauche sans tie-break)
La probabilité de gagner un set sans tie-break est alors, avec p la probabilité de gagner un jeu, et q=1-p :
![]()
L'équation avec tie-break est finalement plus simple à déterminer, mais il reste la probabilité de gagner dans un tie-break :
![]()
(Avec T la probabilité de gagner un tie-break, p celle de gagner un jeu, et q=1-p)
La probabilité de gagner un tie-break (7 points à gagner, avec 2 d'avance) en fonction de la probabilité de gagner un point, est la suivante :
![]()
Sous forme de graphe, cela nous donne deux courbes qui se ressemble pas mal :

A gauche, la probabilité de gagner un set avec tie-break en fonction de celle de gagner un point ; à droite, la même chose, mais pour un set sans tie-break.
La domination du plus fort se fait encore plus grande !... (avec ma proba de gagner un point de 1/3, ma proba de gagner un set ne dépasse pas 0,13% !)
Qu'en sera-t-il à l'issue du match... Suspens !
Étape trois : gagner le match
Cette fois, le tableau des différentes issues possibles est plus simples :

Combinatoire d'un match : dans le cas 2-2, le dernier set sera sans tie-break.
Et donc, la probabilité de gagner un match est de :
![]()
où: p est la probabilité de gagner un set avec tie break
p' est la probabilité de gagner sans tie break
q=1-p (la probabilité de perdre un set avec tie break)
Mis sous forme de graphique, cela donne ça :
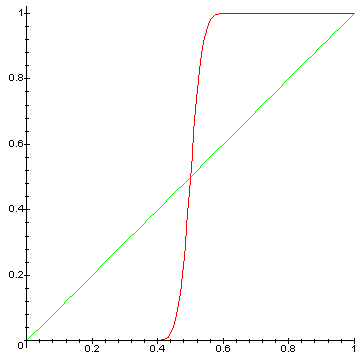
Probabilité de gagner le match on fonction de la proba de gagner un point
Le graphique est éloquent : je n'ai aucune chance contre Federer! Seulement une chance sur 37 millions !
En fait, même avec une probabilité de réussir un point est de 43%, on ne dépasse pas les 1% de chance de gagner le match. Le système de points du tennis a beau être complètement incompréhensible, il permet au plus fort de gagner à coup sûr, même s'il n'est plus fort que de peu. Le secret de Roger est là : il est un tout petit peu plus fort que ses adversaires ! Au dernier match, Monfils a gagné 45% des balles, et s'est donc logiquement fait laminer !
Au détail près que tout ces calculs ne rendent absolument pas compte de l'avantage du service, de la dimension psychologique, des spectateurs qui perdent leur chapeau sur le terrain ou d'éventuelles blessures...
Sources :
L'algèbre du tennis - Pour la science n°127, mai 1988



/http%3A%2F%2Fstorage.canalblog.com%2F34%2F53%2F210892%2F87542982_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F78%2F68%2F210892%2F54140207_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F90%2F03%2F210892%2F40119504_o.png)
/https%3A%2F%2Fassets.over-blog.com%2Ft%2Fcedistic%2Fcamera.png)