La nuit au musée
(Cet article aurait du être posté la semaine dernière, mais suite à de nombreux évènements indépendants de ma volonté, le voici posté aujourd'hui)
Les journées européennes du patrimoine : c'est comme un premier dimanche du mois, sauf que ça tombe tous les ans à le troisième week-end de septembre. C'est surtout l'occasion de découvrir l'exposition permanente sur les mathématiques à la cité des sciences, de contempler la salle de pi au palais de la découverte, ou simplement, de se régaler de l'exposition sur les maladies des mouches au muséum d'histoires naturelles...
Le principal problème d'un musée ouvert un jour de gratuité, c'est l'affluence record, qui demande aux gardiens une vigilance accrue pour protéger les œuvres ornant les différents murs. C'est dans ce cas (on ne peut plus concret...) qu'intervient le problème des gardiens de musée (alias, problème de la galerie d'art) :
Combien faut-il au minimum de gardiens pour surveiller un musée ?
Question...
Prenons par exemple la galerie d'exposition Palm Gügg :

Plan de la galerie Palm Gügg, qui possède 14 murs
Le conservateur de l'exposition, Maacx Prabda, souhaite protéger son musée en embauchant le minimum de gardiens. Une fois en position, un gardien n'est plus en mesure de se déplacer, mais sa vision est à 360° (il a le droit de tourner la tête). A tout moment, il faut impérativement que chaque cm² du musée soit dans la ligne de mire d'au moins un des gardiens. Chaque gardien sera posée en un sommet de la galerie. Combien au minimum de gardiens Maacx doit-il engager ?
On peut généraliser la question : étant donné un musée à n murs (ie, un polygone à n côtés (ous les murs sont droits), et qui ne forme qu'une seule salle), quel est le nombre de gardiens suffisant pour le surveiller ? C'est le problème, posé par Victor Klee en 1973, et résolu peu de temps après par le mathématicien tchèque Václav Chvátal (d'où l'appellation "théorème de Chvátal" pour ce problème).
C'est à ce moment là de l'article que l'on prend un papier et un crayon, que l'on dessine à la va vite quelques plans de musée, et que l'on cherche à placer un minimum de gardiens. Après, on cherche à conjecturer la solution, et pour les plus courageux, on cherche des pistes pour le démontrer.
C'est bon ? Tout le monde a essayé ? On peut donc maintenant passer à la résolution !
Prenons d'abord le musée du peigne, un musée qui possède 3m murs.
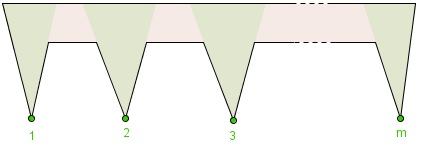
Le musée du peigne et ses 3m murs : il peut être surveillé par m gardiens.
Pour surveiller les sommets des dents, il faut au moins un gardien dans chaque zone verte : il y a m dents, donc il faudra au minimum m gardiens. On peut alors surveiller ce musée en utilisant seulement m gardiens, en plaçant un premier gardien dans le couloir en haut à gauche, et tous les autres en chaque dent du peigne de 2 à m.
En modifiant un peu cet exemple (en enlevant 1 ou 2 murs) , on peut trouver pour tout n (≥3) un musée à n murs demandant ⎣n/3⎦ gardiens. (⎣x⎦, c'est le plus petit entier inférieur ou égal à x). Ca montre que ⎣n/3⎦ gardiens peuvent dans certains cas être nécessaires.
En fait, on ne peut pas faire de musée plus tordus :
⎣n/3⎦ gardiens suffisent toujours pour surveiller un musée à n côtés
Puisque la galerie d'exposition Palm Gügg possède 14 murs, on peut la surveiller avec seulement ⎣14/3⎦=4 gardiens. La preuve par l'image :

Seulement 4 gardiens pour surveiller la galerie
(Les plus observateurs trouveront une solution en seulement 3 gardiens, cf le premier commentaire de Antoche)
Démonstration...
Pour une fois, la démonstration n'est ni trop longue, ni trop technique : elle est donc tout à fait blogable ! La démonstration qui suit n'est pas la démonstration originale de Chvátal, mais celle de Steve Fisk (5 ans après).
La première chose à faire, c'est de trianguler le musée : relier deux à deux des sommets du musée pour ne former que des cellules triangulaires. Sur l'exemple, ça donne ceci :
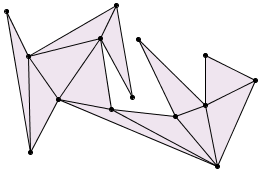
Une triangulation de la galerie Palm Gügg
On obtient alors un graphe, qui a la particularité d'être 3-colorable : on peut colorier chaque sommet en rouge, bleu ou vert de manière à ce qu'une arrête ne relie jamais deux sommets d'une même couleur. Ceci se démontre facilement par récurrence : si le graphe ne possède que 3 sommets, il est clairement 3-colorable. Sinon, il possède au moins une diagonale d, qui sépare le graphe en 2 sous-graphes plus petits. Par hypothèse de récurrence, ces sous-graphes sont 3-colorables, et quitte à permuter les couleurs, elles se correspondent sur la diagonale d : bref, le graphe est 3-colorable.

Une 3-coloration du graphe
Parmi l'une des trois couleurs bleu, rouge et vert, l'une d'elle (au moins) sera sous-représentée. Disons qu'il s'agit de la couleur bleue. Alors, les les sommets bleus représente au pire un tiers des sommets : il y a au plus ⎣n/3⎦ sommets bleus. On place alors les gardiens aux sommets bleus. Puisque chaque cellule triangulaire possède au moins un sommet bleu, chaque cellule sera bien gardée par au moins un gardien. CQFD (Ce Que Fisk Démontra)
Bon, en fait, la démonstration possède une subtilité non négligeable : qui a dit qu'un polygone était toujours triangulable ? Certes, tous les polygones sont bien triangulables, mais ce n'est pas quelque chose de complètement évident ! En 3 dimensions, il existe des polyèdres que l'on ne peut pas tétraèdriser...
Pour montrer ça, on suit le même raisonnement que juste avant : il suffit de montrer que dans un polygone a au moins 4 côtés, il y a toujours une diagonale qui le coupe en deux. Dans un tel polygone, la somme des angles vaut (n-2)180° ; il y a n sommets, donc il y a au moins un sommet A qui fait moins de 180° ("convexe"). Si on peut relier entre eux ses deux sommets voisins A et B, alors cette diagonale marche. Sinon, c'est qu'il y a un mur dans le passage, et donc, au moins un sommet D dans le triangle ABC, qui fait une extrémité parfaite pour une diagonale que l'on recherche.

Le sommet A est convexe. A gauche, la diagonale BC est dans le polygone : tout baigne. A droite, il y a au moins un point D dans le triangle ABC, qui fournit une diagonale DA.
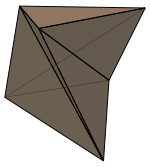
Le polyèdre de Schönhardt, composé à l'aide de deux triangles équilatéraux parallèles reliés de façon inattendu, ne peut pas être décomposés en tétraèdres sans rajouter de sommets. Deux autres exemples de polyèdres non tétraèdrable.
Généralisation...
Il n'y a pas un problèmes de maths que l'on ne cherche pas à généraliser, et celui-ci ne fait pas exception !
Il y a d'abord le cas où les angles de la galerie d'art sont tous droits : avec exactement le même raisonnement, on peut montrer que ⎣n/4⎦ suffisent. On commence par montrer que le musée à 4m murs du peigne orthogonal demande m gardiens, et on finit par montrer par récurrence qu'un quadrangulant le musée par des polygones convexes, on obtient un graphe 4-colorable... (L'existence de la quadrangulisation n'est pas forcément évidente...)

Le musée du peigne orthogonal, à 4m murs, demande au minimum m gardiens
De manière plus générale, une galerie d'art à m murs orthogonaux demande au maximum ⎣n/4⎦ gardiens (1980)
Ensuite, il y a le problème de la forteresse : on ne cherche plus à garder l'intérieur de la galerie, mais l'extérieur. Cette fois-ci, il faut bien plus de gardiens : il en faut ⎡n/2⎤ au moins, et ⎡2n/3⎤ au plus (1983) ! On peut le concevoir en cherchant à garder une forteresse convexe : il faut placer au moins un gardien en un sommet sur 2.
Avec une forteresse à murs orthogonaux, il faudra ⎡n/4⎤+1 gardes...
On peut aussi penser aux généralisations impliquant des gardiens qui se déplacent (le long de murs ou de diagonales), aux galeries avec piliers, aux galeries étoilées, etc. Parmi ces généralisations, de nombreuses solutions sont encore au stade de conjectures...
En 3 dimensions, le problème est encore pire : on peut trouver des musées dans lequel placer un gardien en chaque sommet ne suffit pas !
Sources :
Raisonnement divins, Martin Aigner, Günter M. Ziegler
Art Gallery Theorems and Algorithms, par Joseph O'Rourke (la dernière page résume les solutions de toutes les variantes possibles et imaginables)



/http%3A%2F%2Fstorage.canalblog.com%2F72%2F92%2F210892%2F113119539_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F00%2F91%2F210892%2F107069165_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F33%2F48%2F210892%2F101190494_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F83%2F38%2F210892%2F101168363_o.png)