Pick et Pick et Colégram

Qu'est ce qu'un beau théorème ? Si on regarde les premiers résultats de Google (qui a toujours raison), on trouve que cette appellation peut désigner le théorème de Zafar (provenant d'un obscur groupe chez Facebook), le théorème du point fixe de Brouwer, le théorème des accroissements finis, le théorème de Ptolémée, un théorème de Newton sur les coniques, le théorème "femme=problèmes", le théorème de Pascal... A chacun sa propre définition de la beauté d'un théorème.
Pour l'article d'aujourd'hui, un théorème beau, ça sera un théorème qui sort de nulle part, qui ne va nulle part non plus et qui est suffisamment simple pour être compris par un élève en fin de primaire : un un mot, le théorème de Pick !

D'habitude, pour mesurer l'aire d'un polygone, on utilise des formules de la forme longueur × longueur (du genre "longueur du côté au carré" ou "petite base plus grande base fois hauteur divisé par 2"). C'est qu'une histoire d'analyse dimensionnelle : pour trouver une aire, c'est mieux de multiplier des longueurs. La formule de Pick, elle propose mieux : mesurer des aires sans avoir recours à des multiplications !

Pour ça, il faut considérer des polygones simples, du genre de celui-ci :

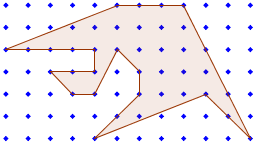
Un polygone simple

Ici, simple signifie que tous les sommets tombent pile-poil sur le quadrillage. Il faut aussi que le polygone ne soit pas "croisé". A partir de là, on compte le nombre n_int de points à l'intérieur du polygone, et n_bd le nombre de points sur le bord du polygone. Le théorème de Pick dit tout simplement que l'aire A du polygone est donné par la formule :

Bref : on peut calculer une aire seulement en comptant les points. Exemple en image :

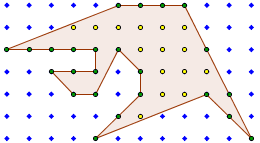
On a 15 points intérieurs (en jaune), 24 points sur le bord (en vert), ce qui donne une aire de 15+24/2-1 = 26 (unités carré).

C'est le moment parfait pour parler de la vie de Mr Pick, qui a établit ce théorème en 1899 : il s'appelle Georg, il est autrichien, il est né en 1859, il a appris la géométrie différentielle à Albert Einstein et il est mort en 1942 dans le camp de concentration de Theresienstadt.

Démonstration !
On a de la chance, ce théorème n'est difficile ni contractuellement, ni dans sa démonstration (d'où sa présence sur ce blog, dans cette série de note sur les petits théorèmes de géométrie combinatoire) !

La démonstration repose sur deux faits essentiels :
(1) le théorème est vrai sur les triangles
(2) si le théorème est vrai sur un polygone, il reste vrai quand on ajoute un triangle à ce polygone

Puisque tout polygone peut être découpé en plein de petits triangles (une triangulation, cf là), la récurrence montre que le théorème est tout à fait vrai.

Une triangulation du polygone :
si on montre que le théorème est vrai sur les petits triangles et que la formule peut s'additionner, ça sera gagné

(1) Prenons un triangle simple : par une habile adjonction de triangles, on peut le transformer en rectangle dont les côtés sont parallèles aux axes.

Il n'y a plus qu'à montrer que la formule est vraie sur les rectangles, sur les triangles rectangles, et quand on enlève les triangles au rectangle.

Pour le rectangle simple, on trouve A_rectangle  = n_int + (n_bd-4)/2 + 1
Pour le triangle rectangle simple, on trouve n_bd = 1 + m+n + k

Sur les rectangles, la formule est à peu près claire : les n_int points intérieurs (rouge) donnent chacun un carré unité, les  (n_bd-4) points du bord (verts) donnent chacun un demi-carré unité, et les 4 points dans les coins (bleus) donnent chacun un quart d'unité, d'où A_rectangle = n_int+(n_bd-4)/2+1 = n_int+n_bd/2-1. Ca, c'était la façon intuitive de procéder.
Autre façon de faire, plus rapide : on suppose que c'est un rectangle m×n. On a alors n_int=(m-1)(n-1) et n_bd=2m+2n. En développant  n_int+n_bd/2-1, on trouve bien mn.
Pour le triangle rectangle, on utilise grosso-modo la même technique, en supposant que sa base est de longueur m et sa hauteur de longueur n. Ce qui est embêtant, c'est de savoir quels sont les points intérieurs du rectangle qui tombent sur la diagonale. Disons qu'il y en a k (sans compter les deux extrémités). Pour ce qui est des points sur le bord, on peut compter qu'il y en a n_bd=1+m+n+k. Les points à l'intérieur du triangle, c'est la moitié des points de l'intérieur du rectangle qui ne sont pas sur la diagonale, autrement dit, n_int = [(m-1)(n-1)-k]/2. Il n'y a plus qu'à développer  n_int+n_bd/2-1 pour trouver mn/2.

La dernière étape, c'est de montrer que la formule est valable par soustraction.

Cet article contient deux fois la même illustration

On a donc encadré notre triangle T par trois autres triangles T₁, T₂ et T₃, pour former le rectangle R. On va appeler i, i₁, i₂, i₃ et i_R le nombre de points intérieurs à T, T₁, T₂, T₃ et R, et on appelle b, b₁, b₂, b₃ et b_R les points des bords. Il nous faut vérifier Aire(T) = i+b/2-1.
Premier chose à dire : il y a autant de points sur les bords de T₁, T₂ et T₃ qu'il y en a sur les bords de T et R, ce qui donne b+b_R=b₁+b₂+b₃.
Deuxième chose à dire : les points intérieurs de R, c'est les points intérieurs de tous les triangles présents, plus ceux sur les bords de T sans être au sommet (il y en a b-3). Autrement dit : i_R = i₁+i₂+i₃+i + (b-3).
La formule A(T)=Aire(R)-Aire(T₁)-Aire(T₂)-Aire(T₃), après application des formules de Pick vus dans le cas particulier des rectangles et des triangles rectangles et des deux égalités juste au-dessus permettent de conclure...

(2) Bref, la formule de Pick est vraie sur tous les triangles... La plus grosse étape de la récurrence est passée, (l'initialisation) il n'y a plus qu'à montrer l'hérédité. On suppose donc que le polygone Q sur qui on veut démontrer la formule est découpé en un triangle T et un polygone P :

On suppose que la formule est vraie sur le polygone P : Aire(P) = i_P+b_P/2-1
La formule est vraie aussi sur le triangle : Aire(T) = i_T+b_T/2-1
On va appeler k le nombre de points intérieurs sur lequel passe le segment séparateur, ce qu permet de trouver une formule pour le nombre de points intérieurs à Q, i_Q=i_P+i_T+k. Puisque ces k points ne sont pas sur le bord de Q, et que deux points sont comptés deux fois, on trouve que b_Q=b_T-k + b_P-k - 2 (=b_T+b_P-2k - 2).
On termine en développant Aire(Q)=Aire(T)+Aire(P) :

Aire(Q) = Aire(T) + Aire(P)
= i_T+b_T/2-1 + i_P+b_P/2-1
= [i_P+i_T+k] + []/2 -1
=  i_Q+b_Q/2-1

Fin de la démonstration : la formule de Pick est indubitablement vraie sur n'importe quel polygone simple !

Généralisations ?
Comme toujours, un théorème aussi cool ne peut pas rester sans être généralisé !

D'abord, il y a la généralisation aux polygones (simples) avec des trous (simplement polygonaux aussi) :

Un exemple de polygones à trous

S'il y a n trous, la formule devient tout simplement :

Dans le cas présent, puisqu'il y a 4 trous, 16 points intérieurs et 110 points sur le bord (si j'ai bien compté), on peut dire que l'aire du polygone est de... 74 !

Et une généralisation en 3 dimensions, pour les polyèdres ? On en 4 dimension, ou plus ? On aimerait bien, mais... non... Et on peut même le prouver ! Il suffit de regarder les tétraèdres de Reeve, dont les sommets sont (1,0,0), (0,1,0), (0,0,1) et (1,1,n), où n est entier. Quand on change la valeur de n, on change le volume du polyèdre ; par contre, il y aura toujours seulement 4 points sur le bord, et 0 points à l'intérieur...

Une autre démonstration !
La démonstration était sympa, mais un peu longue, quand même... On peut le démontrer bien plus rapidement, en utilisant la formule d'Euler ! (Celle qui dit que sur un graphe planaire, si on appelle s le nombre de sommets, a le nombre d'arrêtes et f le nombre de faces (en comptant la face formé par l'extérieur), on a l'égalité f-a+s=2)

Bref. Partageons le polygone en plein de petits triangles qui utilisent tous les points du réseau. Ca peut donner quelque chose qui ressemble à ça :

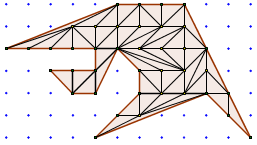
Cette triangulation fait apparaître f-1 petits triangles, chacun d'aire 1/2. D'où Aire(Q)=(f-1)/2.
Les sommets du graphe, c'est l'ensemble des points intérieurs et des points du bord : s=n_bd+n_int .
Chacun des f-1 triangles possède 3 arrêtes ; chacun des a_int arrêtes intérieures bordent 2 triangles, et chacune des a_bd arrêtes du bord n'en borde qu'un seul. Autrement dit, 3(f-1)=2a_int + a_bd . (et donc, f=3-2(a-f)-a_bd (*) )
D'un autre côté, on peut voir qu'il y a autant d'arêtes sur le bords que de points sur le bords : a_bd=n_bd

Il n'y a plus qu'à mélanger toutes les égalités en gras : en appliquant Euler sur (*), on trouve

f = 3 - 2(s-2) - a_bd
= 3 - 2(n_bd+n_int-2) - n_bd
= 2 n_int + n_bd -1

Et, finalement, Aire(Q) = (f-1)/2 = n_int + n_bd/2 -1... Ouais ! CECQJV(R)D ! (C'est ce que je voulais (re)démontrer)

Et il y a forcément d'autre moyens de le démontrer... Mais il commence à être tard, et va falloir poster...

---

Sources :
Pick's theorem, par Tom Davis
La formule de Pick, par Isabelle Jalliffier-Verne, Marc Laforest, dans le dernier Accromaths
Raisonnement divins, par Martin Aigner, Günter M. Ziegler

Comments

[msaoruiruiss]

Ah oui, je le souviens avoir lu cette méthode dans un livre de maths en CM1/CM2, et ça m'avait fasciné à l'époque!

Encore un très bon article, comme toujours!

[ibrahim]

Bonjour,

J'ai apprécié votre démonstration de la formule de Pick.

Cependant, la dernière partie relative à la formule de Euler, je souhaite obtenir, si possible, des détails. en effet, je ne comprends pas à partir de :

3(f-1)=2aint + abd . (et donc, f=3-2(a-f)-abd (*) ).

Pouvez-vous approfondir cette partie ?