Nahal Chaitin

Il y a des nombres qui ne brillent plus ; des nombres dont tous les secrets ont été dérobés par des mathématiciens avides de connaissance ; des nombres qui au fil des années ont perdu toute la magie que les anciens leur attribuaient...
Mais tout n'est pas si sombre ! Un nombre féérique persiste ! Un nombre dont la seule connaissance transformerait un benêt en oracle ; un nombre qui pourrait anéantir le monde par la simple évocation de ses décimales ; un nombre béni des anges , mais qui ne doit jamais tomber entre de mauvaises mains : son nom, c'est Ω  !

Médaillon frappé par Stephen Wolfram en l'honneur de Gregory Chaitin et de son Ω

Prolégomènes
Ahem. Ce que je veux dire, c'est qu'il existe un nombre avec des propriétés plus qu'étonnantes : il est défini sans aucune ambiguïtés, mais il est théoriquement impossible de calculer ses décimales (ou alors, seulement quelques unes).
Ce nombre (ou plutôt, ces nombres), c'est Ω, le grand Omega de Chaitin, inventé dans les années 70 par Gregory Chaitin.

Premier fait : il existe des nombres non calculables.
Grosso modo, un nombre réel, c'est un nombre tel qu'on se l'imagine bien, qui possède un développement décimal infini. Parmi les nombres réels, on distingue les entiers naturels (0, 1, 2, ...), les entiers relatifs (..., -2, -1, 0, 1, 2, ...), les nombres rationnels (les fractions, comme 1/2 ou -8/5 )... Ces ensembles sont dénombrables : on peut décrire leurs éléments sous la forme d'une liste (infinie), moyennant des artifices plus ou moins raisonnables.

Il y a aussi l'ensemble dénombrable des nombres algébriques (les nombres comme √2 ou le nombre d'or, qui sont les racines de polynômes à coefficients rationnels). Puisque l'ensemble des nombres algébriques est dénombrable et que l'ensemble des réels ne l'est pas, il existe des nombres réels qui ne sont racine d'aucun polynôme. Même s'il en existe une (très grosse) infinité, il a fallu longtemps avant que l'on puisse en donner des exemples (π, pour ne citer que le plus connu des nombres transcendants).

Mais il y a aussi l'ensemble des nombres calculables : ce sont les nombres dont il existe un algorithme capable d'en égrainer les décimales. N'importe quel nombre qui pourrait nous venir spontanément en tête est calculable : 14/33, sin(57), π, la solution de cos(x)=x... Quand on parle d'algorithme, on sous-entend une suite finie de caractères ('a', 'b', 'c', ..., '1', '2', ..., '+', '-', '=', ...) qui, dans votre langage de programmation préféré (Pascal, C, Javascript, Maple, Brainf*ck, Ook!, Whitespace, Malboge, ..., du moment qu'il soit assez puissant), égrainera une à une les décimales du nombre en question. L'ensemble des programme est dénombrable, si bien qu'il n'existe qu'un nombre dénombrable de nombre calculables. Conséquence : il existe des nombres (et même une infinité indénombrable) incalculables !

Deuxième fait : le problème de l'arrêt est indécidable
Piochons un algorithme au hasard dans la liste (P₁, P₂, P₃, ...) des programmes corrects écrits dans tel langage de programmation. Il y a alors deux possibilités : ou bien le programme s'arrêtera (en ayant ou non affiché quelque chose à l'écran), ou bien le programme tournera en boucle. Pour savoir dans quel cas on se trouve, on est tenté de lancer l'algorithme. S'il s'arrête, on peut conclure, mais s'il ne s'arrête pas, on ne peut pas être sûr de savoir s'il est en train de boucler ou s'il est simplement long. La seule façon de s'y prendre est d'analyser finement la structure de l'algorithme.
Cette procédure n'est pas automatisable : il n'existe aucun programme capable d'analyser des programmes de façon à déterminer s'il s'arrêtera ou non. En ce sens, le problème de l'arrêt est dit indécidable.

Grâce à ce théorème, on peut fabriquer un nombre qui n'est pas calculable, un petit oméga de Chaitin. Étant donné un langage et la liste (P₁, P₂, P₃, ...) de ses programmes, on pose ω = 0,d₁d₂d₃..., où d_i = 0 si le programme P_i s'arrête, et 1 s'il boucle indéfiniment. Le nombre ω est parfaitement défini, mais est de fait incalculable !

Le grand Ω de Chaitin
Bien que difficiles à appréhender, les ω possèdent tout de même une infinité de décimales que l'on sait calculer. Les nombres Ω, par contre, ne possèdent qu'un nombre fini de décimales calculables (et encore, on ne peut pas savoir combien). Il y a même pire, les Ω de Solovay, dont aucune décimale ne peut être calculée...

La définition des Ω fait évidemment appel au problème de l'arrêt, et est défini comme "la probabilité d'arrêt d'une machine universelle auto-délimité". Une machine universelle (un programme, en gros) est auto-délimité quand il est terminé par un caractère ou un mot spécial, du genre "STOP". Ainsi, pour tirer au hasard un programme,  il suffit de tirer aléatoirement des caractères jusqu'à obtenir "S.T.O.P".

Bon, pour simplifier, on va dire qu'un programme est une suite de 0 et de 1 qui termine par 1111 (la traduction binaire de "STOP"). En tirant à pile ou face chaque chiffre, on finit par obtenir un programme valide de longueur n. Un programme donné de longueur n a ainsi une probabilité de (1/2)ⁿ. de sortir. Selon cette procédure, quelle est la probabilité de sortir un programme valide et qui ne boucle pas indéfiniment ? La réponse à cette question, c'est Ω.

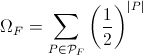
où P_F est l'ensemble des programmes qui terminent, et |P] est la longueur de P.

Ce nombre (ou plutôt, ces nombres) étant défini à partir du programme de l'arrêt, il n'est pas calculable...

Cela dit, il y a quand même moyen de calculer quelques-unes de ses décimales (Il y a moyen de l'approcher par l'expérience, puisque Ω est une probabilité ; on peut aussi chercher à savoir si les petits programme s'arrêtent ou non). Cela dit, même si quelques décimales peuvent être connues, on n'en aura jamais une infinité. En 2002, Calude, Dineen et Shu se sont amusés à calculer les 64 premiers chiffres binaires de Ω, pour une machine universelle U créée pour l'occasion. Le résultat, c'est que P_U = 0.00787499699...

En gardant la même construction, mais en changeant un peu la machine utilisée, Robert Solovay est parvenu à construire un nombre parfaitement défini dont aucune décimale ne pourra jamais être connue !

Cela dit, bien que l'on ne connaisse pas ses décimales, on sait un max de choses sur lui :

* Ω est non calculable, et donc irrationnel et transcendant.
* Presque tous ses chiffres sont indécidables : son 151e chiffre est soit 0, soit 1, mais la théorie des ensembles est incapable de le dire.
* Ω est un nombre univers dans toute les bases : n'importe quel suite de chiffre apparaît quelque part dans le développement décimal (ou binaire) de Ω. Et même plus, Ω est normal dans toute les bases : la fréquence d'apparition d'une séquence de k chiffre est de 1/10^k.
* Ω est aléatoire : le plus petit programme qui peut écrire les n premières décimales de Ω a une taille proportionnelle à n.
* Si on retire une décimale sur 2, une décimale sur 3 ou les décimales ayant une position première, les propriétés ci-dessus sont encore vraies !

A titre de comparaison, π est calculable, ses chiffres sont décidables, n'est pas aléatoire, et on est incapable de dire si c'est un nombre normal ou univers (même si on se doute que oui).

Qui connaît Ω contrôlera le monde
Ou, du moins, contrôlera le monde des mathématiques, ce qui est déjà pas mal.
Dans les décimales de Ω sont inscrites toutes les réponses de tous les problèmes mathématique que l'on peut se poser !

Imaginons. Vous êtes mandaté par Dieu, et êtes le garant des décimales de Ω dans un langage de programmation qu'il vous aura préalablement bien expliqué. Un mathématicien vous met au défi de démontrer qu'il existe une infinité de nombres premiers jumeaux. En 23 caractères, vous réussissez à écrire un programme qui énumère de tels nombres premiers. Si ce programme tourne indéfiniment, c'est que la conjecture des nombres premiers jumeaux est vraie.

Mais vous connaissez Ω ! Vous connaissez p, la proportion des 2²⁴ programmes de moins de 23 caractères qui s'arrêtent. Il suffit donc de lancer en parallèle ces 2²⁴ programmes. Après un certain temps, p programmes se seront arrêtés, et les autres ne s'arrêteront pas. Si le programme qui teste la conjecture des nombres premiers ne s'est pas arrêté, c'est que la conjecture est vraie !

En fait, pour n'importe quelle question du genre "peut-on démontrer truc ?", on peut écrire un programme qui s'arrête si et seulement si la réponse à la question est oui. Autrement dit, Ω donne un moyen théorique universel pour répondre à toutes les questions que se posent les mathématiques !

Un Nombre pour les gouverner tous, un Nombre pour les trouver,
Un Nombre pour les amener tous et dans les ténèbres les lier...
[Le seigneur des anneaux factoriels]

---

Sources :
Complexités. Aux limites des mathématiques et de l'informatique, Jean-Paul Delahaye.
The Halting Probability Omega:Irreducible Complexity in Pure Mathematics, Gregory Chaitin

Comments

[H]

Attention, mon premier « énumérer » n’était pas « énumérer récursivement » ; autre façon de dire la même chose : la définition « le nombre obtenu par le procédé diagonal appliqué aux nombres définissables » n’est pas une définition correcte, du moins pas tant qu’on ne restreint pas suffisamment la notion de « définissable » pour (entre autres) qu’elle n’inclue pas cette définition !

[H]

Mais non El Jj, « science étonnante » a raison : il y a bel et bien une quantité dénombrable de textes mathématiques (potentiels) qui définissent sans équivoque un nombre réel.

On ne peut par contre pas les énumérer (ce qui interdit d’utiliser le procédé diagonal). Ton argument ne tient pas. Pour prendre un autre exemple, tu évoques les nombres calculables, il n’y a aucun paradoxe à la Richard dans cette notion, parce que là encore ils ne sont pas (récursivement) énumérables.

Attention, c’est genre de considération qui font devenir constructivistes, on frise l’excommunication à tout moment ! :D

[ScienceEtonnante]

Oui justement il me semblait que la définition d'un nombre tel que tu le proposes n'est pas formalisable dans le langage de départ.

Si tu te donnes une fois pour toute un ensemble de symboles (1,2,x,+,-,il existe,pour tout, etc.), que tu écris l'ensemble des nombres conceptualisables et que tu appliques la diagonalisation, tu récupères un nombre que tu ne peux pas écrire comme suite finie de symboles du langage initial.

Du coup en faisant la diagonalisation on a peut être une construction univoque pour un humain (capable de passer à un méta-langage) mais pas pour une machine, ce qui nous ramène probablement à la notion de nombre calculable d'ailleurs.

Ceci dit l'idée doit rester valable : si tu veux écrire un billet sur un nombre, tu n'as qu'une suite finie de caractère à écrire dans ton article, donc il y a bien une infinité non-dénombrable de nombres dont tu ne pourrais même pas parler si tu le voulais.
Ca te fait pas flipper du point de vue de ta liberté individuelle de mathématicien ? ;-)

[El Jj]

ScienceEtonnante > Le problème de l'arrêt étant parfaitement formalisable, les nombres Omega le sont aussi. Ma définition est heuristique puisque, de toutes façons, je ne maîtrise pas assez le formalisme pour en donner une définition abstraite...
Par contre, avec cette histoire de nombres conceptualisables, on tombe dans le paradoxe de Richard : puisqu'il y en a un nombre dénombrable, on peut en faire une liste, mais en faisant une extraction diagonale, on peut fabriquer un nouveau nombre qui n'est pas dans la liste, et donc pas définissable. (Alors que l'on vient de le définir sans équivoque)

[ScienceEtonnante]

Il y a peu, je m'étais demandé si le concept de "nombre conceptualisable" existait ?

Par exemple si un mathématicien rencontre un autre mathématicien et qu'il veut lui parler d'un certain nombre qu'il trouve intéressant, pour le définir de manière univoque, il va utiliser une suite finie de caractères dans un langage formalisé. Et à toute suite finie de ce type on peut associer un entier selon une procédure classique.

Du coup il n'y a qu'une infinité dénombrable de "nombres conceptualisables", et surtout une infinité non-dénombrable de nombre non-conceptualisables. C'est à dire des nombres qu'on ne pourra jamais évoquer, dont on ne pourra jamais discuter, et sur lesquels tu ne pourras jamais écrire de billets ! (je trouve ça terrifiant)

Ceci dit je me demande si ces nombres omega rentrent dans la catégorie des nombres conceptualisables. Est-ce qu'on peut en donner une définition mathématique sans équivoque en n'utilisant qu'une suite finie de symboles ? Ou est-ce qu'on ne peut en donner qu'une définition heuristique en langage naturel ?