Partons scier

C'est la fête aux partitions ! En l'espace de quelques semaines, deux conjectures de combinatoire ont été résolues. La première, c'était la conjecture q-TSPP, relative aux partitions planes totalement symétriques. L'autre, c'est le problème du nombre de partitions d'un entier, résolues par les fractales. Rien que ça !

Parti-quoi ?
Prenons le nombre 5 : combien y a t-il de façon d'écrire 5 comme la somme d'entiers positifs ? C'est ce que l'on appelle le nombre de partitions de 5 (noté p(5)).  En cherchant attentivement, on peut en trouver 7 :

5 = 1 + 1 + 1 + 1 + 1
5 = 2 + 1 + 1 + 1
5 = 2 + 2 + 1
5 = 3 + 1 + 1
5 = 3 + 2
5 = 4 + 1
5 = 5

Trouver le nombre de partitions de 5,  c'était encore facile. Mais comment faire pour trouver celui de 10 ? Celui de 100 ? Celui de 5000 ?

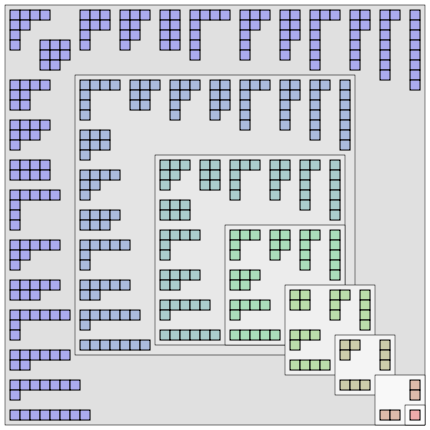
Représentation graphique par les diagrammes de Ferrer de toutes les partitions de 1 à 8.
Par exemple, le diagramme le plus en haut à gauche représente la partition 8 = 4 + 2 + 1 + 1

La façon la plus élégante de traiter le problème est de passer par les séries génératrices ; c'est ce qu'avait compris Euler dans les années 1750. Voyons un problème plus simple : combien y a t-il de façons de payer 1€ en utilisant des pièces de 1, 2 et 5 centimes ? Pour résoudre ça, il faut considérer les séries génératrices (une généralisation infinie des polynômes) suivantes :

G₁(q) = 1 + q + q² + q³ + q⁴ + ... + qⁿ + ...
G₂(q) = 1 + q² + q⁴ + q⁶ + q⁸ + ... + q²ⁿ + ...
G₅(q) = 1 + q⁵ + q¹⁰ + q¹⁵ + q²⁰ + ... + q⁵ⁿ + ...

Ce qui est chouette avec ces séries, c'est que ça se multiplie comme des polynômes. On peut ainsi calculer les premiers termes du produit G = G₁×G₂×G₅ :

G(q) = 1 + q + 2q² + 2q³ + 3q⁴ + 4q⁵ + 5q⁶ + 6q⁷ + 7q⁸ + 8q⁹ + 10q¹⁰ + ... + 541q¹⁰⁰ + ...

Si on regarde de plus près, le coefficient de qⁿ correspond au nombre de façons d'obtenir qⁿ en multipliant un terme de G₁, de G₂ et de G₅. Vu autrement, c'est le nombre de façons de payer n centimes avec des pièces de 1, 2 et 5 centimes (et on peut conclure qu'il y a 541 façons de payer 1€ avec des pièces de 1, 2 et 5 centimes). Avec un peu d'astuce, ce calcul peut se faire à la main, mais un ordinateur permet facilement de résoudre ce problème de combinatoire

Revenons aux partitions de n : p(n) désigne aussi le nombre de façons de payer n€ quand on dispose de pièces de 1, 2, 3, 4, ..., n euros (en supposant qu'elles existent). Transcrit dans le langage des séries génératrices, p(n) est le coefficient de qⁿ dans la série G = G₁×G₂×G₃×...×G_n. En utilisant le fait que G_n(q)=1/(1-qⁿ) (les fameuses séries géométriques), on trouve la formule d'Euler :

Avec un peu de volonté, on peut trouver à la main que p(10)=42. En forçant avec un ordinateur, on trouve que p(100) = 190 569 292. Pour ce qui est du calcul de p(1000), Maple refuse de se lancer dans les calculs, et je le comprends (alors qu'en fait, tout le monde sait que p(1000)=24 061 467 864 032 622 473 692 149 727 991).

La formule d'Euler donne un résultat exact, mais n'est guère pratique. La quête d'une formule utilisable est alors lancée !

Il faudra attendre les années 1900 pour que Hardy et Ramanujan donnent une formule facile à calculer de p(n)

La formule en question n'est pas exacte, mais elle permet de trouver facilement des valeurs approchées. Ainsi, on trouve par cette formule que p(1000) est de l'ordre de 24×10³². Ramanujan inventera d'autres estimations du même genre (mélangeant énigmatiquement des racines, des fractions ou diverses constantes fondamentales), toujours plus fines. Ces formules sont pratiques, mais ne donnent pas de valeurs exactes.

Il faudra attendre les années 1930 et Rademacher pour avoir une nouvelle formule permettant le calcul. Celle-ci ressemble à :

Oui, la formule est exacte, mais est en pratique aussi utile que celle d'Euler (le A_k(n) cache des difficultés calculatoires qu'il ne vaut mieux pas révéler, sans compter sur les sinh ou les π amenant à des valeurs approchées).

A ce moment là de l'histoire, une formule utilisable et précise donnant p(n) reste encore un Graal de la combinatoire...

Une formule pour p(n)
Voici donc l'annonce faite en janvier dernier par l'américain Ken Ono : son équipe a découvert une formule utilisable de p(n) qui donne sa valeur exacte ! La formule en question utilise tout de même des maths plutôt avancées, si bien que le fait de dire qu'elle est

ne nous avance pas...
La découverte de cette formule, ils la doivent à une autre découverte : les partitions de nombre sont... fractales !

Quoi ? Quel rapport entre des nombres et les fractales ? En faisant preuve de suffisamment d'abstraction, on peut s'apercevoir que, sous un certain sens, la suite p(n) est périodique. De là à parler de comportement fractal... Au moins, ça fait parler. Cette périodicité se retrouve à l'état d'embryon chez Ramanujan, quand il démontrait au début du XXe siècle que :

p(5n+4) est divisible par 5
p(7n+5) est divisible par 7
p(11n+6) est divisible par 11

Pour ce qui est de la formule en elle même, elle semble plutôt efficace, à en croire l'explication de Ono sur son fonctionnement :

Je peux prendre un nombre, le mettre dans P, et instantanément calculer la partition de ce nombre. P ne renvoie pas de nombres abominables avec une infinité de décimales. C'est la formule finie et algébrique dont nous étions tous à la recherche.

La conjecture q-TSPP
La deuxième conjecture résolue, c'est celle de George Andrews et David Robbins, datant des années 80. Elle parle des partitions planes totalement symétriques ("Totaly Symetric Plane Partitions"), et a été cassée par 3 mathématiciens de l'Université Rutgers en janvier dernier (Koutschan, Kauers et Zeilberger).

Une partition plane, quesécé ? En reprenant l'image des diagrammes de Ferrer, c'est une généralisation à 2 dimensions de la partition d'un entier. On peut les définir par un tableau de nombres entiers (positifs) qui décroissent de gauche à droite et de haut en bas. Géométriquement, ça correspond juste un tas de cubes entassés dans un coin !

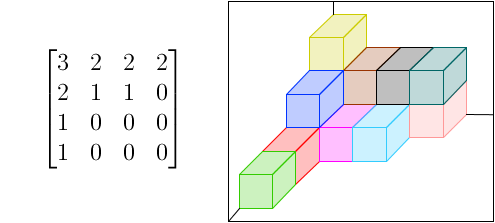
Une partition plane, et le tas de cubes qui lui est associé

Pour ajouter un peu d'harmonie à tout ça, on parle plus précisément des partitions planes totalement symétriques. Ce sont celles qui correspondent aux tas de cubes qui restent inchangés quand on permute les axes. Elles possèdent alors beaucoup de symétries.

Une des 352 partitions planes totalement symétriques qui rentrent dans une boîte 5×5×5. Par symétries, certains cubes s'identifient, par groupes de 6, 3 ou 1.

Le nombre de PPTS qui entre dans une boîte n×n×n est connu depuis 1995, il est donné par la formule suivante (la formule de Macdonald's-Stembridge) :

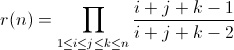
On peut ainsi calculer que r(1)=2, r(2)=5, r(3)=16, r(4)=66, r(5)=352, ... (A005157)

Mais la conjecture s'intéresse plus particulièrement aux orbites. Dans le tas de cubes donné en exemple, on s'aperçoit que certains cubes s'identifient par symétrie, que l'on appelle orbites. On trouve ainsi 4 groupes de 3 cubes (les cubes rouges, verts, dorés et 3 cubes cachés), 1 groupe de 6 cubes (en bleu) et 2 groupes de 1 cube (le noir et l'un des cubes cachés). On compte donc 7 orbites. La question que l'on est en droit de se poser est celle de savoir, parmi les q(n) PPTS qui entrent dans la boîte n×n×n, combien comptent exactement m orbites.

La conjecture, aujourd'hui théorème, d'Andrews et Robbins nous dit que ce nombre r(n,m)est donné par

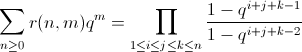
En prenant n=5, on trouve le polynôme suivant, de degré 35 :

1 + q + q² + 2q³ + 3q⁴ + 4q⁵ + 5q⁶ + 7q⁷ + 8q⁸ + 10q⁹ + 12q¹⁰ + 13q¹¹ + 15q¹² + 17q¹³ + 18q¹⁴ + 19q¹⁵ + 20q¹⁶ + 20q¹⁷ + 20q¹⁸ + 20q¹⁹ + 19q²⁰ + 18q²¹ + 17q²² + 15q²³ + 13q²⁴ + 12q²⁵ + 10q²⁶ + 8q²⁷ + 7q²⁸ + 5q²⁹ + 4q³⁰ + 3q³¹ + 2q³² + q³³ + q³⁴ + q³⁵

On en conclut qu'il y a 7 PPTS entrant dans la boîte 5×5×5 qui possède 7 orbites, ou bien 20 qui possèdent 17 orbites...

Une fois n'est pas coutume, la démonstration de cette conjecture s'est faite avec l'aide de l'outil informatique, si bien que la démonstration n'est pas aussi belle que l'on aurait aimé l'avoir. Sans doute une meilleure démonstration existe, le jeu n'est pas terminé.

---

Sources :
De bonnes infos sur les partitions d'entier sur Wikipédia (d'où provient l'illustration)
l-adic properties of the partition function et An algebraic formula for the partition function, où Ono parle respectivement du comportement fractal et de la formule de p(n). L'info a été relayée entre autres par The Language of Bad Physics.
A proof of George Andrews' and David Robbins' q-TSPP conjecture, l'article de Koutschan, Kauers et Zeilberger annonçant la nouvelle. L'info a été relayée par Pour la science.

Comments

[H]

Ouff, je suis allé voir le papier, et ça me rappelle des souvenirs dont je ne sais guère s’ils sont bons ou mauvais... en tout cas ils sont lointains :)

[sorbet]

merci pour ces news.
Un moyen utile aussi pour le nombre de partitions est la transformée d'Euler http://mathworld.wolfram.com/EulerTransform.html
(voir le dernier paragraphe). On peut grâce à elle calculer p(1000) en 6 secondes sur une machine modeste.

[H]

Wououououou je sens que ma pile de biblio-à-faire-que-je-n’aurai-jamais-le-temps-de-faire va s’alourdir... Merci pour ce billet passionnant, j’en étais resté à Euler !