Tout sur la bat-équation
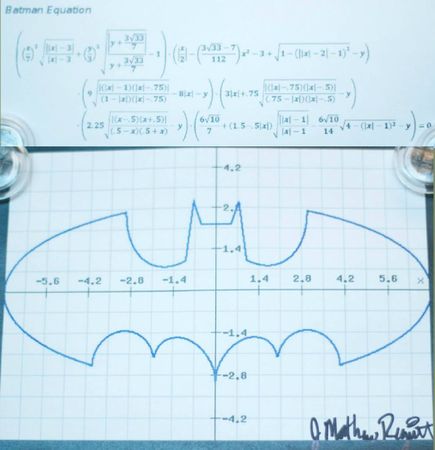
C'est LE buzz du moment, le phénomène Internet qu'il ne faut pas rater : l'équation de Batman ! De quoi je parle ? Eh bien, je parle de ça :
La silhouette de la mystérieuse chauve-souris de Gotham City résumée en une simple équation, c'est complètement possible, et ça a été fait ! Oui, mais... L'équation code-t-elle vraiment l'identité secrète de Bruce Wayne ? Comment fonctionne-t-elle ? Comment puis-je rentrer l'équation dans ma TI-92 ? Qui est ce Mathew qui a signé cette équation ? De nombreuses questions qui trouveront peut être leur réponse dans la suite de cet article !
Fake ou pas fake ?
C'est la première question qu'il faut se poser : cette équation, est-ce du lard ou du cochon ? Eh bien, l'équation est parfaitement authentique : si vous la rentrez dans un logiciel suffisament puissant, le bat-signal apparaîtra devant vous ! Quelques remarques toutefois :
- l'équation est implicite, de la forme f(x,y)=0 : ce n'est donc pas une équation du genre y=f(x) que l'on apprend à dessiner sur sa calculette au lycée. Ce n'est pas non plus une équation polaire ρ=f(θ), ni une équation paramétrique (x(t),y(t)), si bien qu'il vous sera difficile de la rentrer dans une simple calculatrice. La courbe correspond à l'ensemble des points (x,y) qui font s'annuler l'équation (Bon, en fait, quand on la regarde de plus près, on s'aperçoit qu'elle n'est pas si implicite que ça).
- l'équation n'est pas si énorme que ça, elle est simplement découpée en six morceaux, qui correspondent respectivement aux ailes, aux pattes, à l’extérieur des oreilles, à l'intérieur des oreilles, au sommet de la tête et à l'intérieur des ailes de la chauve-souris.
- le plus impressionnant de la formule vient des énormes racines carrées contenant une barre de fraction et des valeurs absolues. Celles-ci permettent simplement de délimiter les morceaux de courbe à une région définie de l'espace. Ainsi, le quatrième morceau serait "2.25-y=0" sans cette racine carrée, ce qui code un simple segment plutôt qu'une droite horizontale. La chose serait moins impressionnante si la fonction signe avait été utilisée à la place de la valeur absolue.
- la deuxième chose qui peut impressionner, c'est la présence de constantes comme (3√33)/7 ou (6√10)/7. Ce sont simplement les choses qui arrivent quand on s'amuse à intersecter ce type de courbes, sensiblement algébriques...
Comment ça marche ?
Passons aux choses sérieuses : pourquoi cette équation dessine Batman ? Détaillons-la :
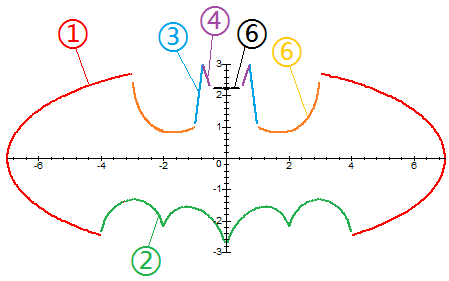La bat-courbe
(1) : Les ailes
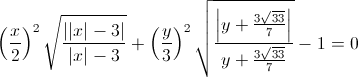
Les ailes, c'est juste une ellipse de grand rayon 7 et de petit rayon 3. L'équation d'une telle ellipse est connue et ressemble à ceci :
Une bat-ellipse
Il ne reste plus qu'à limiter la courbe à la portion de plan qui nous intéresse. On veut x>3 ou -3>x et y>-2.46. Comme ce genre de chose ne se demande pas comme ça à une équation, il faut ruser. Pour cela, le bat-mathématicien utilise la formule suivante :
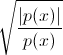
Cette écriture revient à écrire √sign(p(x)). Autrement dit, si p(x) est positif, la formule donne 1 et la courbe apparaît normalement. Si p(x) est négatif, la formule donne i (ou alors, ne donne rien, suivant le sens que l'on donne à la fonction racine carrée) ; en tout cas, la courbe n'apparaîtra pas.
Du coup, il n'y a plus qu'à remplacer p(x) par ce qui nous arrange. Pour que la courbe s'affiche quand x>3 ou -3>x, on prend p(x)=|x|-3. De la même façon, on prend p(y)=y+2.46 pour limiter la courbe au-dessus de la droite d'équation y=2.46. Au final, on obtient ceci :
Les bat-ailes
Les constantes 3 et (3√33)/7≈-2.46 ont été définies a posteriori, en réfléchissant aux points d'intersection de la courbe des ailes avec les autres courbes.
(3), (4), (5) : La tête
Avant de passer aux choses tordues, parlons plutôt de la tête, composée de six segments de droites, dont les équations ne sont pas trop compliquées à déterminer :
y=9-8x (oreille extérieure droite)
y=9+8x (oreille extérieure gauche)
y=0.75-3x (oreille intérieure droite)
y=0.75+3x (oreille intérieure gauche)
y=2.25 (sommet de la tête)
Les deux premières paires d'équations se ressemblent pas mal, à un signe moins près. C'est l'occasion parfaite pour utiliser les valeurs absolues, ce qui ne donne plus que 3 équations :
y=9-8|x| (oreilles extérieures)
y=0.75+3|x| (oreilles intérieures)
y=2.25 (sommet de la tête)
Réunies en une seule équation, ça donne :
Les six bat-droites
Il ne reste plus qu'à limiter ces droites dans le plan pour en faire des segments. La technique reste la même, à base de racines carrées et de valeurs absolues. Ca donne finalement :
L'équation de la bat-tête
Notons qu'il y avait moyen de faire un peu moins compliqué. Pour les paires de segment (3) et (4), on pouvait limiter selon y plutôt que selon x (ce qui enlève plusieurs paires de valeurs absolues dans la formule finale). Pour le segment (5), on peut par contre remplacer p(x)=(0.5-x)(0.5+x) par p(x)=0.5-|x|, ce qui simplifie encore l'équation finale.
(6) L'intérieur des ailes
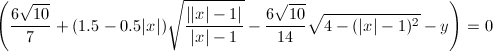
Là, on entre dans les choses sérieuses : une demi-ellipse penchée (linéairement) et symétrisée !
L'équation d'un cercle de rayon 2 et de centre (1,0), ça ressemble à quelque chose comme ça :
Un bat-cercle
Si on ne veut que le demi-cercle du bas, il suffit de mettre les racines carrées et un signe moins là où il faut. Pour symétriser par rapport à l'axe des ordonnées, il faut prendre la valeur absolue de x. Du coup, on trouve ceci :
Deux bat-arc-de-cercles
La partie importante de ce morceau d'équation est ici, tout le reste n'est que fioriture. Le traditionnel mélange de racines et de valeurs absolues permet de limiter la courbe à |x|>1. Le reste permet de distordre le motif pour qu'il colle à la situation (par l'ajout notamment des demies-droites d'équation y=1.5-0.5|x|). Le résultat est alors :
Le bat-intérieur des bat-ailes
(2) Les pattes
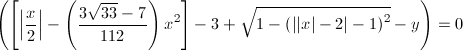
Cette dernière équation permet d'afficher les pattes, et utilise les mêmes idées que pour l'intérieur des ailes, mais en plus poussées. On a cette fois-ci un demi-cercle deux fois symétrisé distordu par deux demies-paraboles symétriques (entre crochets dans la formule).
On commence donc avec un demi-cercle de rayon 1 et de centre (1,0). Son équation ne pose aucun souci :
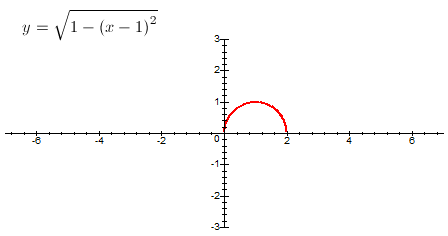
Un bat-demi-cercle
Il faut ensuite le symétriser par rapport aux droites verticales d'équation x=0 et x=2. Pour réaliser ce genre de choses, il faut simplement mettre des valeurs absolues aux endroits adéquats. Comme ça, en fait :
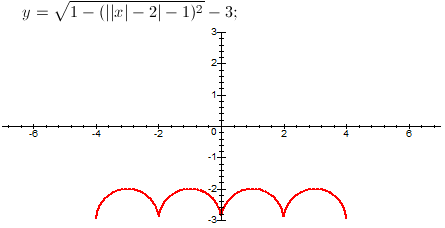
Quatre bat-demi-cercles
Il y a aussi deux demies-paraboles qui entrent en jeu, le truc entre crochet dans l'équation. Celle-ci permet de déformer les quatre demis-cercles. Les coefficients ont été choisis millimétriquement pour que les demis-cercles des pattes s'accordent parfaitement avec l'ellipse des ailes.
Les bat-demies-paraboles
En additionnant le tout, on obtient finalement :
Les bat-pattes
Comment je fais, moi, pour la dessiner sur ma TI-92 ?
Le problème de l'équation, c'est qu'elle est implicite... Seuls les meilleurs logiciels de mathématiques sont capable de dessiner ce genre de choses, et encore, pas très bien (il manque parfois quelques bouts) Heureusement, il n'y a pas grand chose à modifier pour en faire quelque chose d'explicite ! La seule chose qui peut pourrait poser problème, c'est l'ellipse des ailes... Mais si Batman est capable d'arrêter le Joker avec Robin dans les pattes, il n'y a pas de raisons qu'une vulgaire ellipse nous gêne...
Si on regarde les équations des courbes (2), (3), (4), (5) et (6), on voit qu'elles sont de la forme f(x)-y=0. Autrement dit, ce sont des équations explicites de la forme y=f(x) rendues implicites. Il n'y a pas grand-chose à faire pour les remettre dans le droit chemin. L'équation (1) est quant à elle de la forme f(x)-y2=0, que l'on peut rendre explicite avec les équations y=±√f(x).
Bref, si vous voulez réaliser votre bat-signal à la maison, voici les 7 équations à rentrer dans votre calculatrice :
Ces 7 équations seront surement longues à écrire, mais le résultat sera à la hauteur de vos bat-espérances !
Batman approuve cet article
Sources :
Encore plus de discussions sur l'équation du bat-signal ici.
Pour l'équation du logo actuel de Batman (Batman Begins, Dark knight), Anik Trahn vous propose une équation, au moins ausi compliqué que celui de l'ancien logo : ici.
/http%3A%2F%2Fstorage.canalblog.com%2F68%2F79%2F210892%2F119772528_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F43%2F63%2F210892%2F119161093_o.gif)
/http%3A%2F%2Fstorage.canalblog.com%2F74%2F79%2F210892%2F116430959_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F50%2F97%2F210892%2F91694671_o.png)