Manjul Bhargava, celui qui compte

Quand on part en vacances, on se coupe des informations. Parfois par choix, parfois simplement parce que le wifi du camping n'est pas tout à fait fonctionnel. Et quand on rentre de vacances, on découvre que l'on est passé à côté du décès de Robin Williams et de la révélation des nouveaux médaillés Fields. Du coup, je ne sais pas comment les médias ont traité l'hommage au professeur John Keating, à Sean Maguire ou à Alan Parish, ni comment ils sont parvenus à saboter l'événement de l'année de la communauté mathématique.

Rappellons-le : la médaille Fields, c'est comme le prix Nobel, mais pour les mathématiques. Mais elles ne sont remies que tous les quatre ans, contrairement au prix Nobel. C'est donc plutôt les JO des mathématiques. Mais ça n'a rien à voir, d'autant que les Olympiades de mathématiques existentt, et qu'elles ont lieu tous les ans. Mais chaque année, 4 mathématiciens sont récompensés par la médaille Fields, ce qui fait une moyenne de une médaille Fields par an, ce qui est équivalent au prix Nobel. Mais la médaille Fields limite ses récipiendaires à 40 ans, ce qui n'a rien à voir avec le Nobel. Du coup, on n'a qu'à dire que le Nobel des mathématiques est le prix Abel, et que la médaille Fields est la médailles Fields des mathématiques, puisqu'ils ne font jamais rien comme tout le monde.

En cette année 2014, les quatre mathématiciens qui ont reçu la fameuse médaille sont :
- Artur Ávila, franco-brésilien
- Manjul Bhargava, américano-canadien, d'origine indienne
- Maryam Mirzakhani, iranienne, professeur aux USA
- Martin Hairer, autrichien, professeur au Royaume-Uni

Trois choses sont alors à remarquer :
- il faut arrêter de donner la nationalité des mathématiciens, puisqu'ils font vraiment tout pour compliquer les choses
- je n'ai pas encore parlé des lauréats du prix Nevanlinna, du prix Gauss, du prix Leelavati ni de la médaille Chern, remis en même temps que les médailles Fields, mais j'en parlerai (peut-être) dans un futur article
- heureusement qu'une femme et qu'un français ont été médaillés, sinon, on aurait vraiment rien eu à dire

Mais qu'on fait ces 4 mathématiciens pour mériter une médaille ? Commençons aujourd'hui en nous penchant sur les travaux de Manjul Bhargava.

मंजुल भार्गव

Pour situer, Manjul Bhargava est né le 8 août 1974 à Hamilton, au Canada, si bien qu'il avait plus de 40 ans lorsqu'il a reçu la médaille Fields (mais le règlement stipule(rait) qu'il faut être âgé de moins de 40 ans au 1er janvier de l'année du congrès). Il obtient son doctorat en 2001 à Princeton (USA), sous la direction de Andrew Wiles, célèbre pour avoir démontré le grand théorème de Fermat (mais comme il a finalisé sa démonstration à 41 ans, il est passé à côté de la médailles Fields...). Il a donc été récompensé :

"pour avoir développé des nouvelles méthodes en géométrie des nombres, lesquelles ont été utilisées pour compter les anneaux de petits rangs, ainsi que pour avoir borné le rang moyen des courbes elliptiques"

... en géométrie des nombres...
La géométrie des nombres consiste à résoudre de façon géométrique des problèmes issus de théorie des nombres (la théorie des nombres est le domaine où l'on cherche les solutions entières ou rationnelles (les fractions) d'équations).
Par exemple, on peut chercher quels sont les entiers x et y qui vérifient x² + y² = 13. La façon la plus simple de le faire est de dessiner dans un repère le cercle de centre (0,0) et de rayon √13 (autrement dit, le cercle d'équation x²+y²=13), et de regarder où il coupe le quadrillage. Un coup d'oeil rapide permet de vérifier que l'équation possède 8 solutions entières.

Géométriquement, on voit que l'équation x²+y² = 13 possède 8 solutions entières.

On peut également poser la question du nombre de solutions (entières) de l'inéquation x² + y² ≤ 13. Cette fois-ci, il faut compter le nombre de points à l'intérieur du disque de centre (0,0) et de rayon √13.

Géométriquement, on voit que l'équation x²+y² ≤ 13 possède 45 solutions.

En généralisant la construction, on peut voir que si le nombre C est assez grand, l'équation x² + y² ≤ C aura environ π.C solutions entières. En effet, l'équation x² + y² ≤ C correspond à un disque de rayon √C, donc d'aire π.C. Chaque noeud du quadrillage correspond à un carré d'aire 1, qui recouvre à peu près le disque, ce qui nous donne une approximation pas trop mauvaise.

Le cercle d'équation x² + y² ≤ C est d'aire π.C, il contient donc environ π.C noeuds du quadrillages

Autrement dit, une considération géométrique sur l'aire d'un disque nous apporte une réponse à une question de thoérie des nombres. C'est ça, la géométrie des nombres, et c'est pour ça que c'est cool.

... de nouvelles méthodes...
Le principal fait d'arme de Bhargava, c'est d'avoir découvert de nouvelles lois de compositions pour des polynômes. Cette découverte s'est faite en trois étapes :
- il a lu attentivement Disquisitiones arithmeticae, de Carl Friedrich Gauss, où il est entre autre question de composition de formes quadratiques
- il a joué avec un Rubik's Cube 2x2x2, ce qui lui a fait penser que le cube serait parfait pour illustrer le problème de la composition de formes quadratiques (sérendipité !)
- il a réfléchi longuement, et a abouti à la découverte de 13 nouvelles lois de compositions (là où Gauss en a péniblement décrit une).

Gauss s'est donc intéressé aux formes quadratiques binaires, autrement dit, aux polynômes à deux variables où tous les monômes sont de degré total 2. Bref, aux polynômes de la forme :

Q(x,y) = a x² + b xy + c y²
avec a, b, c entiers

On apprend au lycée qu'il existe trois types de trinômes du second degré : ceux qui possèdent deux racines, ceux qui n'en possèdent qu'une seule, et ceux qui n'en ont aucune. Pour savoir à quel type de trinôme on a affaire, on calcule son discriminant :

Δ = b² − 4ac

Lorsque Δ est négatif, le trinôme n'a pas de racine, et c'est là que c'est intéressant. Pour les formes quadratiques binaires, c'est pareil, elles ne sont intéressantes que lorsque Δ est négatif. Et si, en plus, les coefficients a et c sont positifs, on leur donne un nom : les formes quadratiques définies positives.

Une question qui taraude Gauss est de savoir combien il existe de formes quadratiques binaires définies positives (que je vais abrégéer en écrivant simplement "forme", parce que c'est pénible à écrire) différentes ayant un discriminant -Δ donné. Par exemple, quels sont les formes de discriminant -4 ?
Déjà, il y a Q(x,y) = x² + y².
Mais il y a aussi Q'(x,y) = x² + 2xy + 2y²
Ou alors il y a Q''(x,y) = 65 x² + 94 xy + 34 y²
En fait, n'importe quelle forme Q(rx+sy,tx+uy) (avec r,s,t,u entiers tel que ru-st=1) a le même discriminant que Q, ce qui donne une infinité d'exemples possibles 
Du coup, tous ces exemples de formes ne sont pas réellement différents. Ils constituent alors une même classe d'équivalence, à un changement de variable près. Mais y en a-t-il d'autres ? Pour Δ=-4, non, mais ce n'est pas le cas pour d'autres valeurs de Δ.

La question qu'il faut donc se poser est donc plutôt : combien existe-t-il de classes différentes de formes quadratiques, pour un discriminant -Δ donné ? C'est avec des outils de la géométrie des nombres que l'on peut répondre, au moins de manière approximative, à cette question.

Une autre question qui taraudait Gauss était celle de la structure de ces formes quadratiques : y a t-il un opération (une composition) que l'on peut faire entre deux formes qui donnerait une autre forme ? Il y a des façons naïves de le faire (en additionnant deux formes, on trouve une autre forme), mais celles-ci ne préservent pas le coeur de la forme quadratique : son déterminant. Et c'est là que le génie de Gauss, et plus tard, celui de Bhargava, opèrent !

Pour cela, Gauss s'appuie sur un fait bien connu : quand on multiplie deux sommes de deux carrés (x²+y²), on obtient une somme de deux carrés. Par exemple, le produit de 13 (=2²+3²) et de 25 (=3²+4²) est 325 (=6²+17²), tous trois sommes de deux carrés.
Ceci vient du fait que, pour tout nombres x, y, x', y', on a l'identité (x²+y²)(x'²+y'²) = (xx'-yy')² + (xy'+yx')² (on peut l'illustrer en remarquant que le module d'un produit de deux nombres complexes est égal au produit des modules).
Ainsi, en combinant la forme Q(x,y)=x²+y² avec elle-même, on trouve à nouveau cette forme : d'une certaine façon, on peut dire que Q×Q=Q.

On peut voir sur un autre exemple. Il existe seulement deux formes (à équivalence près) de déterminant -12 :
Q₁ = x² + 3y² et Q₂ = 2x² + 2xy + 2y²

On peut alors vérifier que l'on a les identités suivantes :
Q₁(x,y)×Q₁(x',y') = Q₁(xx'-3yy',xy'+x'y) 
Q₁(x,y)×Q₂(x',y') = Q₂(xx'-x'y-2yy',xy'+2x'y+yy') 
Q₂(x,y)×Q₂(x',y') = Q₂(xx'-xy'+2yx'+yy',xx'+xy'+yy') 

Autrement dit : Q₁×Q₁ = Q₁, Q₁×Q₂ = Q₂ et Q₂×Q₂ = Q₁ ! C'est ce que l'on appelle la composition des formes quadratiques, et on peut trouver des formules similaires liant entre eux toutes les différentes forme d'un même déterminant donné. Ces identités sont plutôt obscures, et il fallait au moins le génie de Gauss pour découvrir leur existence. 

Mais là où Bhargava intervient, c'est qu'en reprenant et en améliorant les méthodes de Gauss, il est parvenu à généraliser la composition des formes quadratiques à des polynômes de degré supérieur. Du coup, il a fait passer de 1 à 14 le nombre de lois de compositions connues pour les polynômes, cassant au passage l'idée que de telles identités ne pouvait exister que dans le cas des formes quadratiques.

Outre la satisfaction d'avoir plein de nouvelles identités pour les polynômes de degré 2 ou plus, toutes ces constructions sont utiles pour étudier les corps de nombres, objet central en algèbre.
Un corps, c'est un ensemble dans lequel on peut faire sans problèmes les quatre opérations de base : addition, soustraction, multiplication et division. On peut citer, par exemple, le corps des nombres rationnels ℚ, ou celui des nombres réels ℝ.

Ce que l'on aime bien faire avec les corps, c'est y ajouter des nombres pour voir ce que cela donne (on parle d'extensions de corps). Par exemple, on peut prendre le corps des nombres réels ℝ, et y ajouter un nombre qui serait la racine du polynôme X²+1. Si on appelle cette racine i, on obtient des nombres de la forme a+ib, où i²=-1, autrement dit, le corps des nombres complexes. C'est un corps quadratique de discriminant -4, puisqu'il a été construit à partir du polynôme X²+1.
Ce qui serait génial de savoir, c'est le nombre d'extensions de corps qui existent pour un déterminant donné (plus le déterminant est grand, plus le corps sera complexe). Grâce à Bhargava et à ses lois de compositions des polynômes, c'est chose faite !

(Mine de rien, la théorie des corps est centrale en algèbre, et c'est quand elle a été mise au point que l'on a pu résoudre sans difficulté les 3 grands problèmes de l'antiquité)

...avoir borné le rang moyen des courbes elliptiques...
Deuxième prouesse de Manjul Bhargava (avec Arul Shankar) : avoir borné le rang moyen des courbes elliptiques. Evidemment, rien n'aurait été possible sans tous les outils qu'il venait de mettre au point. Par ce théorème qui a fait sa renommé, Bhargava et Shankar ont fait un pas de plus vers la résolution de la conjecture de Birch et Swinnerton-Dyer, l'un des 7 problèmes du millénaire.

Une équation elliptique, c'est une équation de la forme :

y² + a₁ xy + a₂y = x³ +a₃ x² +a₄ x + a₅
où a₁, a₂, a₃, a₄, a₅ sont des nombres rationnels

Par exemple, les deux equations suivantes sont elliptiques :

y² = x³ +1

y² + y = x³ - x

Encore une fois, le but est de trouver des solutions rationnelles pour ces équations, et surtout, dire combien il y en a : un nombre infini ou pas ?
Dans le cas de l'équation y² = x³ +1, il n'y a que 5 solutions : (-1,0), (0,1), (0,-1), (2,3) et (-2,3)
Dans le cas de l'équation y² + y = x³ - x, il y a une infinité de solutions : (0,0), (1,-1), (1,0), (-1,0), (-1,-1), (2,2), (2,-3), (6,-15), (0.25, -0.375), ...

Mais pourquoi certaines équations elliptiques ont un nombre fini de solutions, et d'autres un nombre infini ? C'est injuste ! Pour cela, on va voir comment déterminer ces solutions, et on va le faire de façon graphique, puisque à chaque équation elliptique correspond sa courbe elliptique :

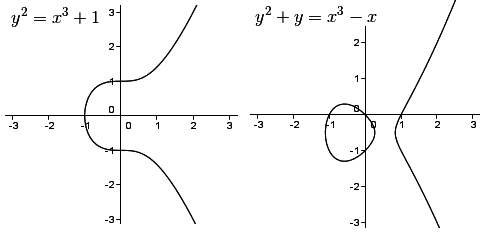
Deux courbes elliptiques

Sur ces courbes, on va définir deux opérations : étant donné deux point P et Q de la courbe, on note :

• P*Q : le troisième point d'intersection entre la courbe et la droite (PQ). Si P=Q, la droite (PQ) est la tangente à la courbe au point P.
• P+Q : le symétrique de P*Q par rapport à l'axe de symétrie de la courbe.
  On peut démontrer que le point P+Q existe toujours, sans aucune ambiguité (le point P+Q peut éventuellement être un point à l'infini)

Pour deux points P et Q de la courbe (distincts ou non), on fait correspondre un point P*Q et un point P+Q.

Ce qui est intéressant avec cette opération, c'est que si P et Q sont des points à coordonnées rationnelles (des solutions de l'équation de départ), alors P*Q et P+Q aussi. On peut donc, si l'on connaît une solution de l'équation, en déterminer d'autres.

Reprenons la première équation : y² = x³ +1. Une solution particulière de cette équation est le point A (2,3).
Pour déterminer le point A+A, on trace la tangente à la courbe au point A. Cette tangente coupe la courbe en A*A = D(0,-1), donc A+A est le symétrique de D par rapport à l'axe Ox, c'est B (0,1).

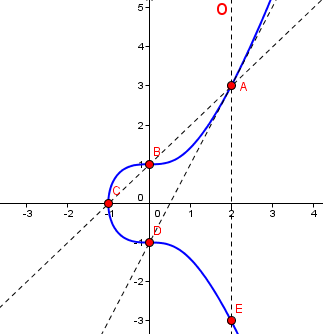
Les 5 solutions rationnelles de l'équation y² = x³ +1

On a donc A*A = D, donc 2A = A+A = B
De même :
A*B = C, donc 3A = A + 2A = A+B = C
A*C = B, donc 4A = A + 3A = A+C = D
A*D = A, donc 5A = A + 4A = A + D = E
Et enfin, A*E = O (le point à l'infini), donc 6A = A + E = O
O est élément neutre, puisque A+O = A.
Les 5 solutions de l'équation y² = x³ +1 sont donc tous les multiples du point A !

Si on part sur la deuxième équation y² + y = x³ - x, les choses se passent légèrement différement. Une solution évidente est la solution A(0,0).
En suivant la même méthode, on trace la tangente à la courbe au point A, ce qui nous donne le point A*A = B'(1,-1), et donc, 2A = B(1,0).

On peut poursuivre : 3A = C (-1,1)
4A = D (2,-3)
5A = E (-0.25, -0.625)
6A = (6,14)
7A = (-5/9 , 8/27)
etc.
En continuant ainsi, on passera par tous les points à coordonnées rationnelles de la courbe, qui sont en nombre infini. Puisque le point A(0,0) permet de trouver l'ensemble infini des solutions de l'équation, on dira que A est un point générateur.

Mais parfois, il arrive qu'un point générateur ne suffise pas pour obtenir l'ensemble des points rationnels de la courbe. C'est par exemple ce qui arrive avec la courbe d'équation y² + y = x³ + x² - 2x, où il est nécéssaire d'avoir deux points générateurs.
Le nombre minimum de points générateurs nécéssaires pour engendrer l'ensemble des points rationnels de la courbe est appellé son rang, et c'est ce nombre qui mesure la complexité de la courbe elliptique que l'on étudie.
Ainsi, la courbe y² + y = x³ - x est de rang 1, la courbe y² + y = x³ + x² - 2x est de rang 2 et la courbe y² = x³ +1 est de rang 0 (puisqu'elle n'a qu'un nombre fini de solution).
Le rang d'une courbe elliptique est toujours un nombre fini, mais n'est a priori pas borné. On ne connaît cependant que très peu de courbes elliptique de très haut rang, le record étant une courbe de rang (au moins) 28, et date de 2006 :

y² + xy + y = x³ - x² - 20067762415575526585033208209338542750930230312178956502x + 34481611795030556467032985690390720374855944359319180361266008296291939448732243429

Les courbes de haut rang sont en fait particulièrement rares, tandis que les courbes de rang 0 ou 1 semblent légions. Mais est-ce toujours le cas ? Si je prend au hasard une courbe elliptique, quelle est la probabilité de tomber sur une courbe de rang 0 ou 1 ? L'expérience montre que environ la moitié sont de rang 0, l'autre moitié de rang 1, et que les rang supérieurs sont négligeables. 
En moyenne (dans un sens que je n'expliquerai pas), on doit donc s'attendre à ce que le rang d'une courbe elliptique soit autour de 0.5. 

Mais la démonstration que le rang moyen est bien 0.5 n'est pas aisée... Ce n'est d'ailleurs aujourd'hui toujours pas démontré, mais on s'approche doucement de cette valeur.
Avant que Bhargava et Shankar ne s'intéressent au sujet en 2010, on s'était arrêté à un rang moyen inférieur à 1.79. Mais la démonstration de cette valeur sous-optimale utilise comme acquis la démonstration de l'hypothèse de Riemann et de la conjecture de Birch et Swinnerton-Dyer (deux conjectures à un millions de dollars que l'on est très loin d'avoir percé).
Aujourd'hui, on sait que le rang moyen des courbes elliptique est inférieur à 1.17, et pas besoin de théorèmes non démontrés pour le prouver. C'est en particulier ce théorème qui a permis à Bhargava d'obtenir la médaille Fields.

Le théorème 290.
Un dernier théorème de Bhargava que j'apprécie tout particulièrement : le théorème 290 ! Il dit la chose suivante :

On considère une forme quadratique définie positive à coefficients entiers.
Si elle peut représenter les 29 nombres suivants :
1, 2, 3, 5, 6, 7, 10, 13, 14, 15, 17, 19, 21, 22, 23, 26, 29, 30, 31, 34, 35, 37, 42, 58, 93, 110, 145, 203, and 290
alors, elle peut représenter n'importe quel nombre entier (on dit qu'elle est universelle).

Par exemple, le polynôme Q(x,y,z,t) = x²+y²+z²+t² est une forme quadratique définie positive à coefficients entiers.
On peut vérifier qu'il existe un moyen d'écrire tous les nombres de la liste avec ce polynôme : 1 = Q(1,0,0,0), 2 = Q(1,1,0,0), 31 = Q(5,2,1,1), etc. D'après le théorème 290, tous les nombres entiers 
Autrement dit, n'importe quel nombre peut être écrit comme somme de (au plus) 4 carrés. Cette propriété porte un nom, c'est le théorème des quatre carrés de Lagrange. Le théorème 290, lui, permet de généraliser le théorème de Lagrange en fournissant un critère d'universalité des formes quadratiques. (à noter tout de même que le théorème de Lagrange intervient dans la démo du théorème 290)
Par contre, le polynôme Q(x,y,z) = x² + y² + z² échoue au test, puisqu'il est impossible d'écrire 7 comme somme de trois carrés : ce polynôme n'est pas universel.

Les 29 nombres de l'énoncé sont optimaux : pour chacun de ces entiers, il existe une forme quadratique représentant l'ensemble des entiers sauf lui. Par exemple, la forme quadratique x² + 2y² + 2z² + 5t² représente tous les nombres, sauf 15 !

Ce critère a permis à Bhargava de compléter la liste des forme quadratiques quaternaires (à 4 inconnues) universelles. Alors que Ramanujan pensait qu'il n'y en avait que 54, Bhargava a montré qu'il y en avait en fait 6436 !

---

Sources
The Work of Manjul Bhargava

Composition and Bhargava's cube, Florian Bouyer

Answers on a donut – the Fields medal lecture of Manjul Bhargava, Rachel Thomas

Universal quadratic forms and the 290-Theorem, Manjul Bhargava and Jonathan Hanke

Manjul Bhargava, médaille Fields 2014, Étienne Ghys
Le rang des courbes elliptiques, François Brunault

Comments

[Tollmann]

Merci pour cet article ! Un détail me paraît toutefois assez obscur : « la courbe y² = x³ +1 est de rang 0 (puisqu'elle n'a qu'un nombre fini de solution) ».

Pourtant, pour engendrer l’ensemble des solutions (même s’il est fini), on a bien besoin de partir d’un point, le point A, non ? Pourquoi ne pas dire alors qu’elle est de rang 1 (et peut être générée par A ou E) ? Il me semble que le seul groupe de rang 0 est le groupe trivial, non ? Et qu’en ce cas, les seules courbes pouvant prétendre à un rang zéro seraient les courbes ne passant que par un point aux coordonnées rationnelles…



Par ailleurs, je serai curieux de savoir ce qu’on entend par rang /moyen/… Puisqu’a priori, l’ensemble des rangs des courbes n’est pas majoré, ne pourrait-on pas trouver de courbes de très haut rang… voire tomber sur un groupe des solutions n’étant PAS de type fini, ce qui rendrait le calcul d’une moyenne quelque peu compliqué… ?