Artur Avila, celui qui mélange

Dans le dernier épisode, j'avais entrepris d'écrire de petits articles pour décrire les travaux de la dernière fournée des médaillés Fields. Dès le premier article sur Manjul Bhargava, j'ai échoué, puisque l'article était trop long. Je vais tenter de me rattraper, en parlant aujourd'hui du plus brésilien de tous les médaillés Fields français (puisque c'est le seul qui soit franco-brésilien) : Artur Avila !

Artur Ávila Cordeiro de Melo

Artur Ávila est né le 29 juin 1979 à Rio de Janeiro, si bien qu'il a été médaillé Fields à moins de 36 ans (ce qui est plutôt rare). En même temps, vu qu'il a démarré sa thèse à 19 ans, il est normal qu'il obtienne la médaille Fields plus tôt que les autres. Cette médaille, il l'a remporté grâce à 

"ses profondes contributions à la théorie des systèmes dynamiques qui ont bouleversé le domaine, en utilisant la puissante idée de renormalisation comme principe unificateur"

Suite logistique
Ce qui intéresse Artur Avila, c'est de comprendre le comportement des systèmes dynamiques : le mouvement des planètes, la dynamique des populations, le mouvement des électrons... Ce qui caractérise un système dynamique, c'est que leur évolution est parfaitement déterministe : la connaissance exacte des conditions initiales permet toujours de savoir leur avenir. Mais si on ne connaît que vaguement les conditions initiales, la prédiction du futur du système est souvent compromise. Mais ce n'est pas une fatalité ! Commençons déjà par étudier le plus célèbre des systèmes dynamiques, issu d'une modélisation de la croissance de populations : la suite logistique.

Pour un nombre réel r∈ ]0,4], on définit la fonction logistique f:x ↦ r.x.(1-x). 
Puis, étant donné un nombre u₀ ∈ ]0,1[, on va observer le comportement de la suite (u_n) définie par u_n+1 = f(u_n).

Malgré son apparence très simple, cette suite peut avoir des comportements très bizarres pour certaines valeurs de r et de u₀.

Prenons un premier exemple, avec r = 2.8 et u₀ = 0.2. Dans ce cas, la suite logistique est la suivante :
u₀ = 0.2, u₁ = f(u₀) = 0.448, u₂ = f(u₁) = 0.692..., u₃ = 0.596..., u₄ = 0.674..., u₅ = 0.615..., u₆ = 0.662...
En itérant davantage, on constate que la suite finit par se stabiliser autour de 0.6428 (9/14). La suite converge !

On peut observer le comportement de ces suites à l'aide de ce que l'on appelle les diagrammes en "toile d'araignée" (ou diagrammes de Vershult). Pour cela, on dessine la fonction que l'on va itérer (ici, f), ainsi que la droite d'équation y=x, et on place le terme initial u₀ sur l'axe horizontal. On va ensuite placer le point u₁ en reliant verticalement u₀ à la courbe de f, puis horizontalement la courbe f à la droite y=x. En répétant l'opération, on fabriquera la "toile d'araignée" qui représentera les différents termes de la suite.
La convergence d'une suite se traduit sur ce diagramme par la convergence des zig-zag.

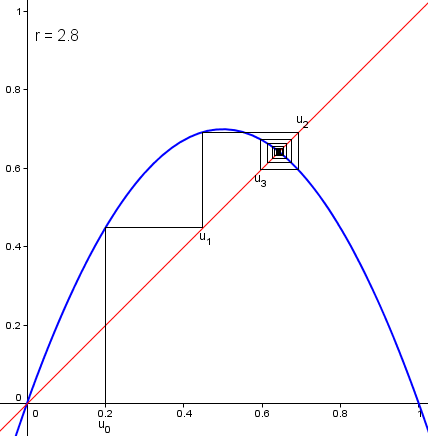
Diagramme en toile d'araignée de la suite logistique, pour r = 2.8 et u₀ = 0.2
Les 500 premiers termes de (u_n) sont représentés (même si 99% d'entre eux sont concentrés autour de 9/14)

En fait, le choix du terme initial u₀ n'a aucune incidence sur le devenir de cette suite de paramètre r=2.8 : elle finira toujours par converger vers 9/14.

Mais pour les autres valeurs de r ? Eh bien, ça dépend...

Déjà, il y a les valeurs r comprises entre 0 et 3 : c'est toujours la même chose qui se passe, la suite converge :

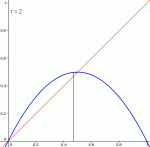
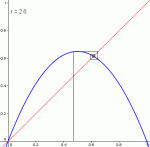
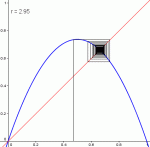
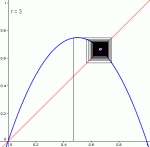
Pour r ∈ ]0,3], la suite converge, quelle que soit la valeur initiale u₀.
Pour r=3, la convergence vers 2/3 est cependant particulièrement lente.

Mais pour les valeurs plus grandes que r=3, les choses se corsent. D'abord, gentiment, lorsque r est compris entre 3 et 3.449 : la suite ne se stabilise pas autour de une seule valeur, mais autour de 2 :

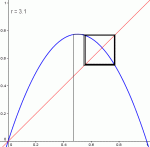
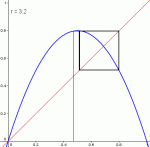
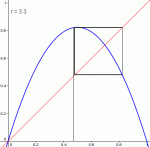
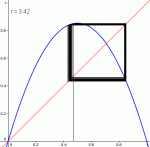
Diagramme pour r=3.1, r=3.2, r=3.3 et r=3.42
Pour r ∈ ]3,1+√6], la suite se stabilise autour de 2 valeurs, quelle que soit (sauf exception) la valeur initiale u₀.

Pour des valeurs encore plus grande de r, ça se complique davantage : la suite se stabilisera autour de 4 valeurs (r ∈]3.449, 3.544]), puis autour de 8 valeurs (r∈]3.544;3.564]), puis autour de 16 valeurs, etc., et ce, tant que r ≤ 3.57.

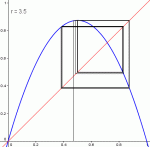
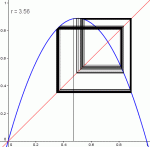
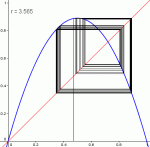
Diagramme pour r=3.5, r=3.56, r=3.565
Pour ces valeurs r ≤ 3.57, la suite finira par se stabiliser autour de 2ⁿ valeurs

Mais pour les valeurs plus grandes que 3.57, le chaos arrive ! Il n'y a plus aucune valeur autour desquelles la suite va se stabiliser. De plus, si on change même très légèrement la valeur initiale u₀, la trajectoire sera complètement différente. On peut alors dire que la suite a un comportement chaotique. Encore une fois, ce chaos est indépendant de la valeur initiale (sauf exceptions)

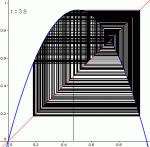
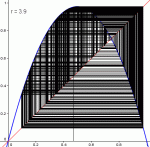
Diagramme pour r=3.7, r=3.8, r=3.9 et r=4
Pour ces valeurs r ∈ [3.57;4], la suite est chaotique : elle ne se stabilisera autour d'aucune valeur

En fait, ceci n'est pas totalement vrai. A partir de r=3.57, on peut trouver parfois des valeurs r pour lesquelles la suite se stabilisera autour de 3 valeurs, autour de 6 valeurs, ou autour de n'importe quel nombre de valeurs choisies à l'avance. Par exemple, pour r=3.83, la suite se stabilise autour de 3 valeurs :

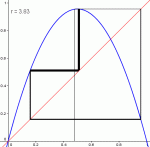
Diagramme pour r=3.83 : la suite se stabilise autour de 3 valeurs.

On peut résumer le comportement de la suite logistique par son diagramme de bifurcation : en abscisse, le paramètre r, et en ordonnée, ses valeurs d'adhérence :

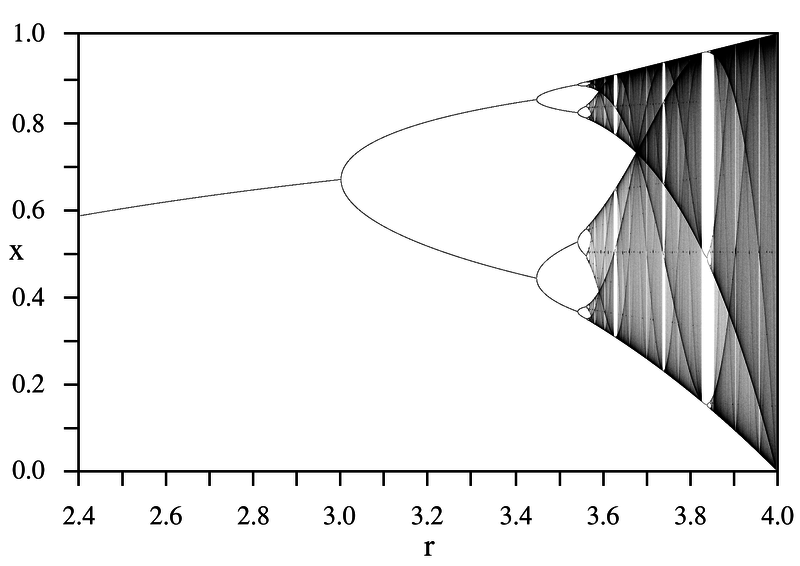
Finalement, la suite peut présenter deux comportements, suivant la valeur r :
- ou bien elle est régulière : elle finit par se stabiliser autour d'une ou de plusieurs valeurs
- ou bien elle est chaotique

Dans le cas où la suite est chaotique, elle n'est cependant pas si imprévisible qu'on voudrait bien le croire. Même si on ne peut pas connaître la valeur de la suite après un grand nombre de valeurs, on peut tout de même prédire avec une certaine probabilité dans quel intervalle elle se trouvera. Par exemple, on peut vérifier que dans le cas r = 0.9, la suite passera plus de 20% de son temps dans l'intervalle [0.9;1], ou qu'elle sera deux fois plus souvent autour de 0.35 qu'autour de 0.7. Et ça, indépendemment du choix de u₀ (sauf, comme toujours, cas particuliers). 
Autrement dit, quand on connaît la valeur r, on peut connaître la répartition des valeurs prises par la suite. Le système dynamique se comporte alors comme un objet aléatoire : on dit alors que la suite stochastiquement stable.

Existe-t-il des valeurs r pour laquelle la suite serait ni régulière, ni stochastiquement stable ? ... Eh bien, oui, mais ces exemples sont négligeables (les cycles attracteurs peuvent par exemple être des ensembles de Cantor...). C'est l'objet du théorème de Lyubich (2002), qui indique que presque toutes les suites logistiques sont régulières ou stochastiquement stable.

Mais ça, c'était juste pour le cas très particulier des suites logistiques. Qu'en est-il de tous les autres systèmes dynamiques ? Eh bien, c'est ça l'objet du travail de Artur Avila : il a démontré, avec Lyubich et Melo, que la plupart des systèmes dynamiques observent cette dualité régulier/stochastiquement stable !

Les échanges d'intervalles
Un autre problème qui a longtemps empêché Avila de dormir est celui du mélange des jeux de cartes (bon, avec un nombre infini et continu de cartes, mais l'idée est là).

Par exemple, pour mélanger un jeu de 32 cartes, on peut répéter plusieurs fois l'opération suivante : faire 4 tas de cartes A, B, C, D, puis les réassembler en mélangeant l'ordre des tas (par exemple, D, A, C, B). Quand on parle de système dynamique, il est nécessaire que l'opération soit toujours identique.

Disons que les tas A, B, C et D contiennent respectivement 7, 7, 7, et 11 cartes. En numérotant les cartes de 1 à 32, on a le découpage suivant :

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

En permutant ces 4 tas selon le motif DACB, on obtient :

22

23

24

25

26

27

28

29

30

31

32

1

2

3

4

5

6

7

15

16

17

18

19

20

21

8

9

10

11

12

13

14

Et si on répète encore la même opération :

18	19	20	21	8	9	10	11	12	13	14	22	23	24	25	26	27	28	4	5	6	7	15	16	17	29	30	31	32	1	2	3
7	15	16	17	29	30	31	32	1	2	3	18	19	20	21	8	9	10	25	26	27	28	4	5	6	11	12	13	14	22	23	24
28	4	5	6	11	12	13	14	22	23	24	7	15	16	17	29	30	31	21	8	9	10	25	26	27	32	1	2	3	18	19	20
10	25	26	27	32	1	2	3	18	19	20	28	4	5	6	11	12	13	17	29	30	31	21	8	9	14	22	23	24	7	15	16
31	21	8	9	14	22	23	24	7	15	16	10	25	26	27	32	1	2	6	11	12	13	17	29	30	3	18	19	20	28	4	5
13	17	29	30	3	18	19	20	28	4	5	31	21	8	9	14	22	23	27	32	1	2	6	11	12	24	7	15	16	10	25	26
2	6	11	12	24	7	15	16	10	25	26	13	17	29	30	3	18	19	9	14	22	23	27	32	1	20	28	4	5	31	21	8
23	27	32	1	20	28	4	5	31	21	8	2	6	11	12	24	7	15	30	3	18	19	9	14	22	16	10	25	26	13	17	29

Après 10 répétitions, le jeu est plutôt mélangé, et c'est parfait pour une bataille ! 
Après un grand nombre n d'opérations, on dira que le jeu est mélangé si, dans n'importe quel petit groupe de carte, la proportion de carte d'un groupe donné est la même que dans le jeu complet.
Autrement dit, un jeu de carte est bien mélangé si, dans une main, on a toujours environ 50% de cartes rouges, 25 % de piques, 12.5% de carte as ou roi...

Il y a quand même un problème avec le mélange d'un jeu de 32 cartes, c'est qu'après un certain nombre de répétitions, on reviendra forcément à un jeu parfaitement trié. En effet, puisque chaque répétition donne une nouvelle permutation des 32 cartes, et qu'il n'existe *que* 32! (=32×31×30×...×1 = 3.2×10³⁵) permutations différentes, on retombera tôt ou tard sur le jeu trié.
Cela signifie qu'il existe des grands nombres d'itérations n pour lesquelles le jeu n'est pas mélangé...

Cependant, un tel mélange par permutation peut facilement se généraliser à des intervalles :

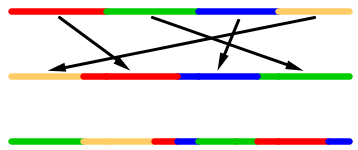
Permutation DACB, itérée deux fois

On peut se poser la même question : est-ce que cette permutation est mélangeante ?
Si oui, cela signifierait que, après plusieurs itérations, la première moitié (ou n'importe quel sous-ensemble) de l'intervalle contiendrait exactement la même proportion de rouge (et des autres couleurs) que dans l'intervalle initial. Une telle perfection de mélange est impossible à obtenir, mais on peut l'exprimer en terme de limite : la limite de la proportion de rouge dans la première moitié de l'intervalle doit tendre vers la proportion initiale de rouge.
Malheureusement, une permutation mélangeante, ça n'existe pas, et c'est à Anatole Katok que l'on doit se résultat. Mais ce que Avila a montré, avec Giovanni Forni, c'est que la plupart des permutations d'intervalles sont faiblement mélangeantes : elles sont mélangentes à condition d'exclure un "petit" nombre de valeurs de n.

Ce résultat sur les intervalles peut s'appliquer sur les billards de forme quelconque, ce qui fournit de précieux résultats dans l'étude des mouvements des particules en physique statistique.

Le problème des 10 Martinis
Il existe des problèmes mathématiques côtés à un million de dollars (les fameux problèmes du prix du millénaire, comme l'hypothèse de Riemann ou le problème P=NP). Et il y en existe pour qui la récompense est à première vue moindre, comme le problème des dix martinis. Comme son nom l'indique, dix martinis seraient offerts en échange de la résolution du problème ; une proposition du mathématicien Mark Kac (proposer une ou plusieurs boissons alcoolisées en échange de la résolution d'un problème étant l'une des coutumes des mathématiciens de l'école de Lwów, en Pologne). A noter qu'il existe une variante plus "sèche" de ce problème, appelé problème des dix dry martini... Le problème des 10 martinis est donc le suivant :

Montrer que, pour tout λ ≠ 0, et pour tout α irrationnel, le spectre de l'opérateur presque-Mathieu 
est un ensemble de Cantor

J'ai retranscrit l'énoncé pour la forme, je ne vais pas le détailler davantage. La seule chose qu'il faut dire, c'est que l'opérateur presque-Mathieu décrit l'évolution d'un électron dans un champ magnétique particulier. Il ne fait nul doute que les physiciens apprécient de connaître le spectre d'un tel opérateur. 

Artur Avila, ainsi que Raphaël Krikorian, Svetlana Jitomirskaya et David Damanik ont résolu ce problème des 10 martinis, ainsi que d'autres problèmes issus de la liste des problèmes de Simon, 15 problèmes issus de la théorie des opérateurs de Schrödinger à destination des mathématiciens du XXIe sicèle. L'histoire ne dit pas si ils ont gagné leur dix verres de vermouth.

L'opérateur presque-Mathieu est lié au papillon de Hofstadter, qui, avant d'écrire des livres (Godel, Escher, Bach), s'intéressait à la physique. Cette fractale issue de la physique représente la conductance de Hall (?) en fonction de l'énergie (??) et du flux magnétique (???). Autant dire que je n'ai pas compris exactement ce qu'est le papillon de Hofstadter, mais comme c'est joli, je ne vais pas me priver de le mettre ici pour conclure cet article...

Le papillon de Hofstadter
Je devrais un jour faire un top 10 des utilisations du papillon en mathématiques...

---

Sources
The work of Artur Avila
La suite logistique et le chaos, Daniel Perrin
Weak mixing for interval exchange transformations and translation flows, Artur Avila et Giovanni Forni

Comments

[Antoine]

Avec un petit programme j'ai vu que que le mélange présenté faisait revenir à la situation de départ après seulement 231 répétitions. Le tout doit être de savoir s'arrêter à temps :)