Don't dead open inside
Le zombie est une créature à capacités cognitives limitées à la fois morte et vivante, se nourrissant essentiellement de cerveaux humains. Ils peuvent se nourrir avec d'autres types de viandes, mais la viande humaine reste quand même leur principale source de protéines. Le mathématicien, quant à lui, est une créature bien vivante dont les capacités cognitives sont potentiellement infinies et qui, sauf rares exceptions, ne se nourrit pas de cerveaux humains, mais plutôt de café.

Pourtant, les mathématiciens entretiennent des rapports très proches avec les zombies dès qu'il s'agit de modélisation. Et la question qui se pose vraiment, c'est de savoir comment réagirait la population mondiale face à une épidémie de type zombie...
Le modèle SIR
Pour modéliser une apocalypse zombie, on peut piocher parmi les modèles classiques d'évolution des population. On penser au modèle proie-prédateur de Lotka et Volterra, mais puisque les zombies sont considérés comme des malades dans la plupart des histoires de zombies modernes, c'est plutôt du côté des modèles épidémiologiques que l'on va se tourner.
Le modèle de base en épidémiologie (qui date tout de même de 1927) duquel dérive la majorité des autres modèles est le modèle SIR. Il part de l'hypothèse que, face à une maladie donnée, le monde se divise en trois catégories : les individus sains et susceptibles de tomber malade (S), les individus infectés (I) et les individus remis de leur maladie (c'est à dire, soit immunisés, soit morts) (R). Evidemment, c'est un modèle, et de très nombreuses variantes ont été proposées et étudiées.
Pour mathématiser le modèle, on va devoir faire appel aux équations différentielles. Pour cela, on va considérer les fonctions suivantes :
- S(t) : le nombre (ou la concentration / proportion) d'individus sains, en fonction du temps
- I(t) : le nombre d'individus infectés, en fonction du temps
- R(t) : le nombre d'individus remis, en fonction du temps
Pour modéliser le problème, on a également besoin de connaître plusieurs coefficients, propres à chaque maladie :
- β, le taux de propagation du virus (plus β est grand, plus la maladie est infectieuse)
- ζ, le taux de rémission ou de décès du virus (1/ζ correspond alors au temps moyen de rémission/décès) (plus ζ est petit, plus le temps durant lequel le malade est contagieux est long)
Ainsi, le nombre d'individus sains diminuera au cours du temps. Cette diminution sera proportionnelle selon le coefficient de propagation β du virus, et dépendra donc du nombre d'invidivus infectés présents (plus le nombre d'infecté est grand, plus la propagation sera rapide). Mathématiquement, cela s'écrit S'(t) = – β.I(t).S(t), où S'(t) désigne la dérivée de la fonction S en fonction de t, qui correspond à la vitesse de diminution du nombre d'individus sains.
Inversement, le nombre d'individus infectés augmente proportionnellement au taux β et au nombre d'individus encore sains, mais diminue selon le taux de rémission ζ. L'équation est alors I'(t) = β.S(t).I(t) – ζ I(t)
Enfin, l'augmentation du nombre d'individus remis/morts est proportionnelle au nombre d'individus infectés, d'un facteur ζ. On a alors l'équation R'(t) = ζ I(t).
Finalement, on obtient un système de trois équations différentielles :

Qu'on se le dise tout de suite, il est hors de question de chercher une formule explicite pour la solution de ce système. Déjà parce que la connaître ne nous apportera pas grand chose, mais surtout, parce qu'une telle formule n'existe généralement pas. On peut quand même étudier le comportement des solutions !
On peut le faire mathématiquement, en étudiant par exemple les points d'équilibre du système. Mais on peut aussi, et c'est quand même plus amusant, choisir des valeurs pour les coefficients β et ζ, ainsi que des conditions initiales, et laisser l'ordinateur faire les calculs pour compter le nombre de morts causés par notre virus fictif (bien sûr, cela implique également de s'y connaître en mathématique de modélisation pour vérifier que les courbes que l'on obtient sont les bonnes, mais on va fermer les yeux là-dessus et faire comme si c'était quelque chose de facile).
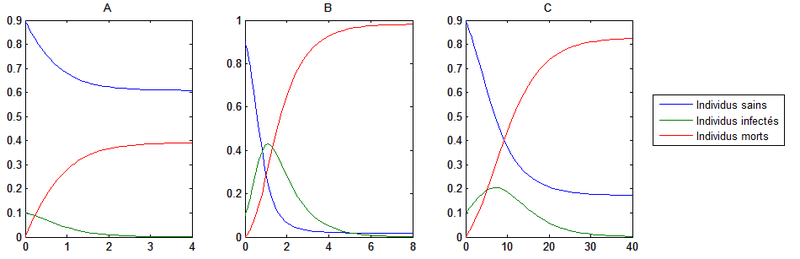
Scénario catastrophe : comment réagirait la population en présence d'un virus mortel et incurable ? Simulons !
A : maladie très infectieuse (β=4) mais rapidement mortelle (ζ=4). 60% de la population survit, c'est pas mal.
B : maladie très infectieuse (β=4) et longtemps contagieuse (ζ=1) : extinction de l'humanité.
C : maladie peu infectieuse (β=0.5) et mais très longtemps contagieuse (ζ=0.25). 20% de survivant !
Dans chaque cas, on part de 90% d'individus sains et de 10% de malades.
Apocalypse zombie, modèle de Munz
Seulement, être un zombie n'est pas une maladie comme les autres puisque, la rémission est rarement possible, et que la mort n'y est que temporaire. Dans un article en 2009, quatre mathématiciens canadiens (P.Munz, I. Hudea, J. Imad et R.J. Smith) proposent une modélisation dérivée du modèle SIR, dans lequel :
- la population I des infectés est remplacée par la population Z des zombifiés.
- on ajoute à l'équation de l'évolution de S un taux de naissance naturel (π) ainsi qu'un taux de décès naturel et/ou de suicide δ (ce qui ajoutera le terme +δ.S à R(t))
- on ajoute à l'équation de l'évolution de Z le terme – α.S(t).Z(t) indiquant la tendance naturelle qu'on les individus sains à attaquer à la hache les individus infectés (ce qui est rarement le cas dans les infections plus classiques), ainsi que le terme + ζ.R(t), indiquant la tendance qu'on les zombies et individus morts à revenir à la vie sous forme de zombie.
- on ajoute à l'équation de l'évolution de R le terme – ζ.R(t), correspondant à la faculté qu'on les morts à revenir à la vie, ainsi que le terme + α.S(t).Z(t) correspondant aux individus débarrasses de leur infection suite à un coup de hache bien placé.
On obtient alors le système d'équation suivant (les "(t)" sont sous-entendus) :

Testons ce modèle avec les coefficients π=0.001, δ = 0.001 (naissances et suicides négligeables), α=1 (humains sains moyennement violents), β=0.5 (zombies peu agressifs) et ζ=0.25 (résurrection des zombies non négligeable), et avec initialement seulement 5% d'e zombies. On obtient les courbes suivantes :
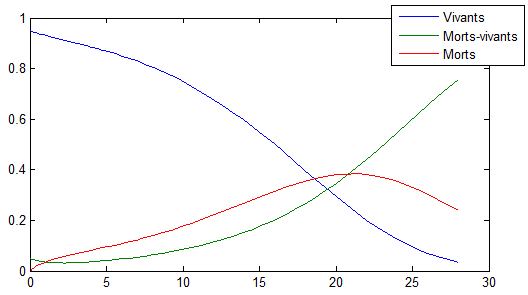
28 jours plus tard, l'humanité a quasiment disparu...
En fait, on peut démontrer que, quelles que soient les conditions initiales, le nombre de zombies tendra vers l'infini. Selon ce modèle, l'apocalypse zombie est inévitable...
Munz et son équipe proposent d'autres modèles dérivés de celui-ci, en envisageant un temps de latence entre la morsure et la transformation en zombie, ou en proposant la possibilité de placer les infectés en quarantaine. Ce modèle possède cependant une énorme faille : les zombies y sont immortels !
Pourtant, il est parfaitement connu qu'un coup de masse, d'arbalette, de fusil, de batte de base-ball ou de n'importe quel objet de tir ou de frappe dans le cortex préfrontal d'un zombie entraîne sa mort définitive. Il faut ajouter une classe au modèle, celui des zombies définitivement morts !
Apocalypse zombie, modèle de Witkowski
En 2013, deux biologistes C. Witkowski et B. Blais proposent une alternative au modèle de Munz comprenant 4 classes :
- S : individus sains
- E : individus en passe de devenir zombie. Ces classes permet d'unifier les différentes formes de zombies selon les oeuvres : chez Romero, la classe E correspond aux morts ; chez Marc Forster, ce sont les 12 secondes d'incubation du virus, etc.
- Z : zombies
- R : zombie définitivement mort
Les interactions entre les différents groupes sont les suivantes :
- Au contact de zombies, les individus sains passent temporairement dans le groupe E, au taux β.
- Les individus du groupe E deviennent inexorablement des zombies, à un taux ζ.
- Les individus sains peuvent, en se suicidant, intégrer directement la classe R, au taux δ.
- En visant la tête, les individus sains peuvent se débarasser définitivement des zombies, au taux α.
Le système d'équation est alors :

On peut alors démontrer que le scénario catastrophe du modèle précédent n'aura pas forcément lieu, dans le cas où α est supérieur à β (autrement dit, si les humains sont plus agressifs que les zombies)
Il ne reste plus qu'à déterminer les coefficients α, β, δ et ζ pour tenter quelques modélisations. Et pour cela, Witkowski et Blais ont fait une petite étude de cas, et ont visionné attentivement La Nuit des morts-vivants (1968, George A. Romero), film qui a donné la définition des morts-vivants, et Shaun of the Dead (2004, Edgar Wright), film où les morts-vivants correspondent parfaitement au stéréotype du zombie moderne.
Pour La Nuit des Morts-vivants, ils ont déterminé α=0.9, β=1.1, ζ=3.6 et δ négligeable. Pour Shaun of the dead, α=0.49, β=0.59 ζ=2 et δ=0. Dans les deux cas, l'humanité finit par périr, contrairement à ce que la conclusion des films laisse à penser...
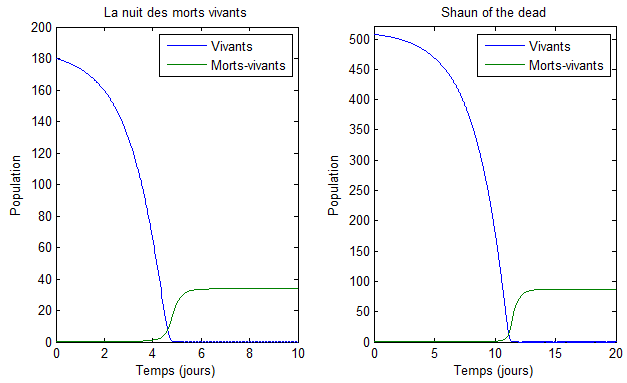
Nombre de vivants et de morts-vivants en fonction du temps dans les deux films, en suivant le modèle de Witkowski
Finalement, face à une épidémie de zombies, toutes les études aboutissent aux mêmes conclusions :
- l'humanité périra,
- quelques humains mieux entraînés que les autres ou en quarantaine survivront peut-être,
- les mathématiciens mourront très vite, trop occupés à déterminer les coefficients de leurs équations différentielles.
Sources :
Bayesian Analysis of Epidemics - Zombies, Influenza, and other Diseases, C. Witkowski et B. Blais
When zombies attack ! : mathématical modelling of an outbreak of zombie infection, P.Munz, I. Hudea, J. Imad et R.J. Smith
Modélisation mathématique, calcul scientifique et zombies, conférence à des lycéens de R. Turpault (il ne se base pas sur le modèle SIR, mais sur l'équation de Lokta-Volterra, puis sur l'équation de Boltzmann)
Image : Will you be ready



/http%3A%2F%2Fstorage.canalblog.com%2F11%2F29%2F210892%2F58500334_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F95%2F86%2F210892%2F41336934_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F10%2F48%2F210892%2F41161995_o.png)
/https%3A%2F%2Fstorage.canalblog.com%2F53%2F79%2F210892%2F134239642_o.png)