2011+1 (Cette nouvelle année est-elle intéressante ? Episode 03)

L'année 2012 est enfin arrivée ! On y croyait plus, et pourtant, elle est là ! Une bonne raison de souhaiter à tous les lecteurs de ce blog une très bonne année...

Oui, mais... Cette année 2012 sera-t-elle plus intéressante que l'année 2011 ? Comme tous les premiers dimanches de janvier, il faut se pencher sérieusement sur la question, avec le seul arbitre digne de confiance, l'OEIS (L'On-Line Encyclopedia of Integer Sequences), l'encyclopédie de toutes les suites de nombres entiers, de la suite des nombres premiers de Mersenne [A000668] jusqu'aux nombres composés dont la somme des facteurs est première [A046363]. Si un nombre donné possède une propriété intéressante, il sera dans l'encyclopédie !

Ainsi, le nombre 2010 apparaît dans 151 suites (11 de plus que l'année dernière, l'encyclopédie est en perpétuelle évolution).  Par exemple, 2010 est un nombre de la forme (n+1)(n+2)(n+3)(9n+4)/24 ([A051798]).
Le nombre 2011, quant à lui, ne possède pas moins de 349 propriétés (18 de plus), la plupart croisant sa primalité avec d'autres propriétés extravagantes. Par exemple, 2011 est le huitième plus petit nombre premier congru à 2 modulo 41 ([A142199]).

Et 2012, alors ? Plus de propriétés que 2011 ? Moins de propriétés que 2010 ? Accrochez vous à votre siège, la réponse ne sera pas agréable, car :

2012 ne possède que 101 propriétés intéressantes !

Pourquoi si peu de propriétés ? Faut-il commencer à déprimer maintenant ? Quel rapport avec le triple A ? Regardons dans le détail quelques propriétés intéressantes du nombre 2012 !

A005341 : La suite de Conway
Enigme : complétez la suite suivante :

1
11
21
1211
111221
...

Oui, bon, tout le monde la connaît, c'est la suite de Conway, où chaque ligne est la description de la ligne précédente. Il se trouve, par le plus grand des hasards, que le 27e terme de cette suite possède 2012 chiffres !

A161328 : la structure des tri-cure-dents
Bien que le nombre 2011 apparaisse dans une suite de structures en cure-dent, 2012 n'est pas en reste. L'objet de base de cette structure n'est plus le cure-dent, mais le tri-cure-dent, un trident formé par 3 segments (angle entre chaque dent : 60°) :

Structure des tri-cure-dents, étape 1 (1 trident)

Trois extrémités sont disponibles : l'étape 2 consiste donc à ajouter 3 nouveaux tri-cure-dents.

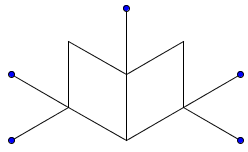
Structure des tri-cure-dents, étape 2 (4 tridents)

Cette fois-ci, il n'y a que 5 extrémités disponibles (et non 9). Pour chaque nouvelle étape, on ajoutera des tri-cure-dents aux places disponibles, sauf si les cure-dents venaient à se superposer.

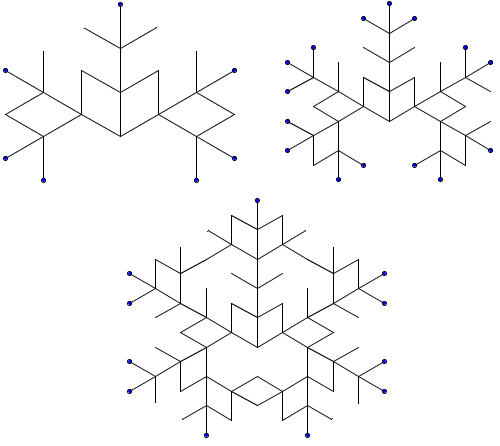
Structure des tri-cure-dents, étape 3 (9 tridents), 4 (16 tridents) et 5 (29 tridents).

En continuant jusqu'à l'étape 42 cette structure, il nous faudra exactement 2012 tri-cure-dents !

A134970 : les nombres canyon
On appelle "nombre canyon" un nombre qui ressemble... à un canyon (une vallée profonde entre deux falaises). Autrement dit, c'est un nombre possédant le même premier et dernier chiffre, et ses chiffres intermédiaires sont rangés par ordre décroissant puis par ordre croissant. Le plus simple, c'est de regarder des exemples : 2012 et 32013 sont des nombres canyon :

 
Canyon (du catalan canyó) : vallée très encaissée résultant de l'érosion hydraulique.

Le 46ème plus petit nombre canyon (et le plus petit nombre canyon à 4 chiffres) n'est autre que le nombre 2012.

Fait intéressant : il n'y a que 116505 nombres canyons, le plus grand d'entre eux étant le nombre 9876543210123456789.

Mais 2012 a encore d'autres propriétés intéressantes. Par exemple :
- le carré du miroir de 2012 est égal au miroir de son carré (comme 2011, en fait) ([A035123]).
- le produit de 2012 et de son miroir est un palindrome : 2012 × 2102 = 4229224 (2011 vérifie la même propriété) ([A048344]).
- 2012, ainsi que 2013, 2014 et 2015, ont exactement 3 diviseurs ([A045940]).
- le nombre de chiffres de 2012! est un carré ([A006488]).
- 2012 possède un mois de février avec 5 mercredis ([A141039]) et 3 "vendredi 13" ([A190653]).

Et la santé !

Comments

[mlmb]

Rien de plus normal: toute année bissextile possède, en février, un jour répété 5 fois; cette année, c'est mercredi. Pas de quoi grimper aux rideaux et décréter que c'est une "propriété intéressante". Plutôt une évidence.

[Dr. Goulu]

@Bernard : ce ne serait qu'une des fameuses 101 propriétés de 2012 listées sous #http://oeis.org/search?q=seq%3A2012



mais il n'y a qu'une série répertoriée comportant 2012,2013,2014 et 1015 et ce n'est pas la votre : http://oeis.org/search?q=seq%3A2012,2013,2014,2015



http://oeis.org/A165936 ne considère pas 2012, ce qui signifie qu'on ne compte pas 2 fois le 2 dans le nombre de diviseurs

[Bernard]

Peut-être pourriez-vous préciser "2012, ainsi que 2013, 2014 et 2015, ont exactement 3 diviseurs premiers"

(encore que pour 2012 pour en compter trois il faut compter deux fois le 2 ...)

Cordialement

[Dr. Goulu]

Un peu dépassé par la vitesse de réaction de 2 lecteurs programmeurs alors que je suis en vadrouille, je confirme que le flocon de Zozoped me semble assez juste pour être déclaré vainqueur (je n'ai pas comptés les 3*2012 cure-dents moi même...)

image sur mon blog.

[RuBisCO]

ElJj, je ne sais pas si tu es au courant, mais Zozoped semble avoir réussi le défi de Dr. Goulu !

J'attends d’avoir la confirmation du maître...