J'aimerais tant revoir Syracuse

"Prenez un entier supérieur à 1.
S'il est pair, divisez le par 2.
S'il est impair, multipliez-le par 3 et ajoutez 1.
Réitérez ensuite les deux précédentes étapes"

Ce qui est surprenant dans cette histoire, c'est que la suite obtenue tombera toujours sur 1, peut importe l'entier choisit au départ.

Et ce qui est encore plus surprenant, c'est que personne ne sait pourquoi !

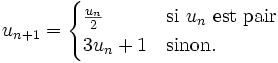
Ce problème est couramment appelé Conjecture de Syracuse. (mais aussi problème de Syracuse, algorithme de Hasse, problème de Ulam, problème de Kakutani, conjecture de Collatz, conjecture du 3n+1 ou plus poétiquement la suite de grêlons)

On a encore beaucoup de mal à en décider la paternité, les tests ADN n'ont pas encore été faits...
En fait, tout commence avec Lothar Collatz, dans les années 1930, qui s'amuse à faire des transformations itératives d'entiers et regarde ce que ça donne.
Dans les années 50, Helmut Hasse se rend à l'Université de Syracuse (près de New York, pas du tout en Sicile) et remporte un grand succès en diffusant son problème.
Pendant la seconde guerre mondiale, le polonais Stanislas Ulam reprend le problème à son nom, et, dix ans plus tard, S. Kakutani reprend le problème pour le diffuser à son tour sous son nom.
Et, dans l'histoire, personne n'a réussit à le résoudre.
A l'époque de la guerre froide, on parlait de ce problème comme d'un complot soviétique pour ralentir les recherches aux États-Unis...
Dans ces années là, un mathématicien hongrois, Paul Erdõs, proposait 500$ à qui arriverait à résoudre le problème (ça vaut pas le millions offert à qui résolverait P=NP...).

Bref, toute cette fabuleuse histoire pour dire que le problème a déjà bien vécu, si bien qu'un joli vocabulaire s'est créé autour du problème.
La trajectoire (ou le vol) d'en entier donné est la suite donnée plus haut.
Le temps de vol, c'est le nombre de terme avant l'apparition du premier 1.
L'altitude maximale est simplement le plus grand terme de la suite.
Le temps de vol en altitude, c'est le nombre de termes nécessaires pour qu'un terme de la suite soit inférieur au premier terme (les plus matheux d'entre vous remarqueront qu'il suffit de démontrer que le temps de vol en altitude est fini pour démontrer la conjecture)
Le facteur d'expansion, c'est simplement l'altitude maximale divisée par le premier terme.

Et pour faire des choses jolies, on peut mettre ça sous forme graphique :

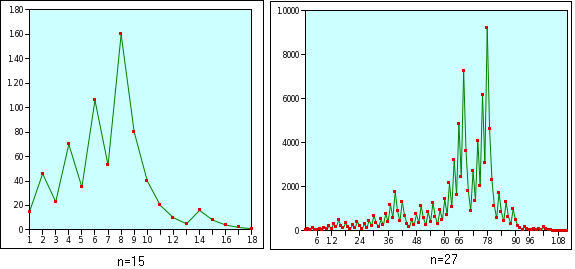
Avec tout ça, vous devriez pouvoir comprendre ce petit script :

 

Nombre de départ :

     

On peut s'amuser à chercher les nombres donnant le plus grand temps de vol, la plus grandes altitude maximale ou le plus long temps de vol en altitude inférieurs à un certain nombre.
Parmi les nombres inférieurs à 100, les champions sont 27 (en altitude maximale et temps de vol en altitude) et 97 (en durée de vol).
Parmi les nombres inférieurs à 1000, les champions sont 703 (en altitude maximale et temps de vol en altitude) et 871 (en durée de vol).
Vous pouvez ensuite tenter de chercher les meilleurs inférieurs à 10000...

En 2004, la conjecture a été vérifiée pour tous les nombres inférieurs à 2⁶⁴ (1,8 × 10¹⁹)
Les seules démonstrations que l'on a réussi a réussi à donner pour l'instant sont heuristiques (statistiques) : en considérant que les nombres impairs, on trouve qu'en moyenne, le prochain nombre impair vaut 3/4 du nombre précédent, ce qui a tendance à décroitre.
En 2006, Alain Slakmon et Luc Macot, mathématiciens québécois se basent la dessus pour donner une démonstration probabiliste de la question, démonstration vraie, mais, comme le signale leur auteurs, "Comme il s’agit d’une approche probabiliste, nous ne pouvons affirmer qu’il s’agit d’une preuve absolument irréfutable de la véracité de la conjecture. Il reste une toute petite possibilité que certains nombres y résistent". Cette possibilité est cependant petite... Mais pas impossible...

---

Sources :
Un site perso et un site moins perso
Article sur la démonstration probabiliste sur CyberSciences

Comments

[titus]

Bonjour
si n multiple de 5, diviser par 5
sinon multiplier par 6, ajouter 1,2,3 ou 4 pour obtenir un nombre divisible par 5
exemple
7,45,9,55,11,70,14,85,17,105,21,130,26,160,32,195,39,235,47,285,57,345,69,415,83,500,100,20,4,25,5,1
On peut aussi multiplier par 6, diviser par 5 et arrondir à l'entier supérieur
exemple
7,9,11,14,17,21,26,32,39,47,57,69,83,100,20,4,5,1
Je ne l'ai pas testée jusqu'à 50 milliards mais il semblerait qu'avec 6 en multiplicateur et 5 en diviseur la suite boucle sur 1
conjecture plus forte
soit m le multiplicateur et d le diviseur
si d est un nombre premier supérieur ou égal à 5,
et m=d+1
si n multiple de d, diviser par d
sinon multiplier par m, diviser par d, arrondir à l'entier supérieur
Pour tout n,la suite boucle sur 1
fr

[fred]

Bonjour
Je pense pouvoir démontrer l'unicité du cycle 4-2-1 dans syracuse, niveau troisième par la théorie des ensembles.
Est-ce-que cela t'intéresse ? A défaut, connait-tu une personne intéressée et parlant français.
La démonstration occupe une page environ.
fred

[Phoenixx]

Aaah ! La conjecture de Syracuse ! Une grande amie qui a su occuper mes heures perdues ... Je la démontrerai, je vous le dis !

[Matthieu]

merci d'avoir parlé de la chute des grêlons, cela me rappelle un de mes premiers sujets d'emerveillement scientifique (et mon premier programme en basic :) ).

[Whiteshoulders]

c'est marrant le facteur d'expension des puissances de 2 ^^