La fabuleuse histoire de tonton Pythagore

"Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés". [Théorème de Pythagore]

Le théorème de Pythagore, c'est la star des théorème de maths ! On le connait au moins depuis l'époque babylonienne (1800 av J-C), mais c'est lorsque Pythagore de Samos (6eme siècle av J.-C.) le démontre (à moins qu'il s'agisse de l'un de ses disciples qui lui a rapporté) qu'il reçoit ce nom (nom donné durant le vivant de Pythagore, la légende raconte qu'il en sacrifia 100 bœufs tellement il en était fier !). Depuis, ce sont des centaines de démonstrations qui en ont été données, Elisha Scott Lomis en réuni 370 dans The Pythagorean proposition.

Selon Euclide - Les Éléments (IIIe siècle av J.C.)
Le mathématicien grec Euclide est le premier à rassembler tous les savoirs mathématiques de l'époque en un seul ouvrage : ses Eléments restent pendant 2 bons millénaires le livre référence de géométrie (et l'un des livres les plus édités, après la Bible). Son crédo : redémontrer toute la géométrie à partir d'un jeu de seulement 5 axiomes (dont le fameux axiome des parallèles). Après un grand nombre de définitions et d'autres théorèmes, c'est à la proposition 47 du livre I d'Euclide qu'apparait pour le première fois le théorème de Pythagore et sa démonstration (ici dans un langage géométrique un peu plus actuel, plus accessible que les tartines d'Euclide, mais tartiné quand même):

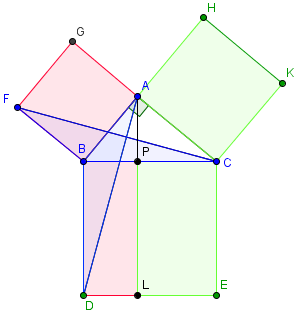Soit ABC triangle rectangle en A : alors le carré du côté BC est égal aux carrés des côtés BA et AC.
On trace les carrés BCED, CAHK et BAGF extérieurs au triangle, les segments FC, AD et AL, parallèle à BD.
{Puisque BAC et BAG sont droits, l'angle GAC est droit : AC et AG sont dans la même direction ; pour la même raison, AB et AH sont dans la même direction.}
Puisque DBC et ABF sont droits, on a FBC=DBA (ABC commun aux deux). On a également BD=BC et BA=BF.
Par l'égalité entre un angle et deux côtés de ABD et FBC, ces deux triangles ont la même aire.
L'aire du rectangle BPLD est double de celle de ABD, car ils ont la même base BD et entre les mêmes parallèles BD et AL (théorème démontré plus tôt par Euclide, dans la proposition 41)
De même, le carré FBAG a une aire double à celle du triangle FBC.
On a d'une part FBC=ABD, et d'autre part, BPLD=2×BDA et GABF=2×FBC : GABF=BPLD.
On montre de même que PCEL=AHKC
On a donc BCED=BPLD+PCEL=GABF+HKCA
Ce qu'il fallait démontrer !

Selon Arnauld - Les Nouveaux éléments de géométrie (1667)
Le livre de Euclide a non seulement été le plus lu, mais également le plus critiqué : il démontre tout dans n'importe quel sens (démontrer un théorème de longueur en utilisant des aires : n'importe quoi !), il fait rien beaucoup trop de démo par l'absurde (le théorème de Pythagore en est une exception), il démontre tout et n'importe quoi, il rend ses lecteurs stupides avec des démonstrations sortis de sous le sabot d'un cheval... Après avoir bien critiqué, Arnauld a forcément du écrire lui aussi ses Nouveaux éléments de géométrie, en démontrant par exemple le théorème de Pythagore sans utiliser d'aires de rectangle :

Avec l'égalités entre les divers angles, on trouve que les triangles ABC, ABD et ADC sont semblables : leur longueurs sont proportionnelles les unes aux autres.

On a donc d/h = n/d = p/b

D'un côté, on a d²/h = n
De l'autre, on a b²/h = m
On a alors, d²/h+b²/h = m+n
C'est à dire : d²+b²=(m+n)h = h²
CQFD !

Selon Clairaut - Éléments de géométrie (1765)
Au XVIIIe siècle, on continue à critiquer Euclide, surtout sur un point : ses démonstrations sont totalement inintéressante ! Comment intéresser le lecteur quand on se la pète en montrant que l'on sait tout sur tout ? Pour Clairaut, il fallait parler directement au lecteur, en lui posant des questions, en reliant les différents problèmes... C'est lui qui a inventé les "démonstrations laissées en exercice au lecteur" (Concept très pratique pour les profs en retard dans leur cours).

Dans la ligne DF, est-il possible de trouver un point H tel que, en faisant tourner le triangle ADH autour de A et EFH autour de E, ils atteignent les positions Adh et Efh, de sortes que ces triangles se joignent en h, et que HEhA soit un carré ?

Oui, c'est possible, si on prend H tel que DH=EF !

S'en suit AHEh = DCda + FEfC (Et, de même, on a le théorème de Pythagore, sur le triangle EFH)

CQFD !

Selon James Abraham Garfield - 1876
On doit à James Abraham Garfield, 20e président des USA (et 1er président gaucher, mais c'est encore plus anecdotique que ce qui va suivre) une démonstration du théorème de Pythagore !

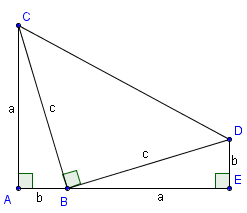La démonstration se base sur la figure juste à côté.

L'aire du trapèze AEDC est (a+b).(a+b)/2 = a²/2 + b²/2 + ab

L'aire de ABC et BED est ab/2
L'aire de BCD est c²/2

Puisque l'aire de AEDC est égale à la somme des aires de ABC, BCD et BDE, on a  :
a²/2 + b²/2 + ab = ab/2 + c²/2 + ab/2
après simplifications : c² = a² + b²
CQFD !

Démonstrations actuelles
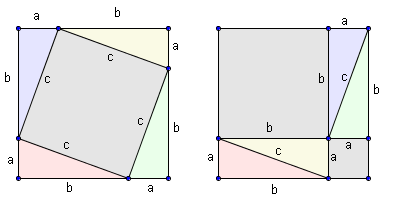
Aujourd'hui, tout livre de maths de 4eme qui se respecte contient une démonstration du théorème de Pythagore (et, normalement, de sa réciproque). La plus classique repose sur la figure ci-dessous. Puisque les deux grands carrés ont la même aire, et que tous les triangles ont la même aire, on en déduit que c²=a²+b².

Mais la manière la plus hype de démontrer Pythagore, c'est d'utiliser les notions plus avancées d'algèbre linéaire ou d'analyse fonctionnelle. Le plan de Euclide, on l'appelle ℝ², (même si n'importe quel espace préhilbertien fait l'affaire...), et démontrer Pythagore se fait en à peine deux lignes :

Soit x,y ∈ ℝ² tels que <x,y>=0
Alors
CQFD

---

Et sinon :
79 preuves du théorème de Pythagore réunies sur une seule page

Comments

[mateo_13]

Bonjour,



merci pour votre article.



Pour information, à destination des enseignants, une axiomatique sous le théorème de Pythagore vient d’être publiée en accès libre :



http://mathemagique-com.blogspot.fr/2014/09/special-profs-une-plongee-sous-le.html



Cordialement,

—

Mateo.