Quatre couleurs, sinon rien !
Séquence nostalgie : il y a exactement quatre ans (±1 jour), j'écrivais ces quelques lignes :
Quitte à commencer quelque part ce blog, je me suis dit que débuter par la première note serait quelque chose de fort judicieux...
A l'époque, j'étais encore jeune, insouciant et ne connaissait rien de la cohomologie singulière. J'avais quelques idées d'articles à faire, pensant tenir au moins quelques semaines au rythme d'un article par jour. L'idée était au moins de passer en revue ce qui constitue la partie émergée de l'iceberg maths : nombre d'or, suite de Fibonacci, un peu de proba, de topologie, le théorème des quatre couleurs, les fractales...
Quatre ans et 218 articles plus tard, je suis encore là (et tout le monde est corda) ! Le rythme est devenu hebdomadaire, le nombre d'or n'a toujours pas trouvé d'intérêt mathématique, le blog est rempli de notes probabilistes et topologiques, le père des fractales est mort... Mais le théorème des quatre couleurs, quant à lui, n'a toujours pas trouvé son droit de cité.
Quatre ans : quatre couleurs ! Il est temps de se prendre en main, et d'enfin évoquer le plus gros pétard mouillé de l'histoire des mathématiques !
Au moins quatre couleurs...
Voici une carte de l'Amérique du Sud. Avec combien de crayons différents, au minium, peut-on colorier cette carte, de façon à ce que deux pays frontaliers soient de couleurs différentes ? Aidez Julien Courbet à résoudre ce problème !
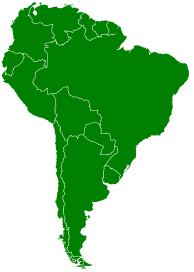
Et plus généralement, si on a une carte quelconque dessinée sur une feuille où tous les pays sont connexes (pas d'îles, pas d'enclaves), combien de couleurs suffisent pour la colorier ?
La réponse ne surprendra personne, puisqu'elle est donnée dans le titre du paragraphe, de l'article, de son intro et dans le nom du théorème : quatre couleurs suffisent. Toujours. Aussi alambiquée la carte soit-elle. C'est cette propriété des cartes que l'on appelle aujourd'hui "théorème des quatre couleurs".

En procédant par tâtonnements, on finit toujours par trouver une solution qui convient.
Si l'océan est un pays, on peut lui attribuer la couleur verte.
On peut même dire plus : dans certains cas comme celui de l'Amérique du Sud, 4 couleurs sont nécessaires. Il suffit de regarder le Brésil, l'Argentine, la Bolivie et le Paraguay : puisque chacun de ces pays possède une frontière avec les 3 autres, il faudra au moins 4 couleurs différentes.
La découverte de cette propriété des cartes remonte aux années 1850. Le botaniste-mathématicien Francis Guthrie, fraîchement diplômé, demande à son ex-professeur Auguste De Morgan (Vous savez, les lois de De Morgan) comment on pourrait démontrer ce qu'il a découvert en examinant la carte des comptés de l'Angleterre. De Morgan n'en sait rien et demande de l'aide à Hamilton, qui lui répond gentiment qu'il tâcherait d'y penser.
Au plus six couleurs...
Le problème des 4 couleurs, c'est avant tout un problème de la théorie des graphes. On peut faire correspondre à la carte un graphe en plaçant un sommet en chaque pays, et en reliant les pays frontaliers. On obtient un graphe planaire, la question est alors : tout graphe planaire admet-il une 4-coloration ?
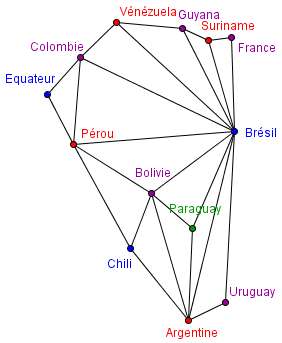
Le graphe qui correspond à la carte de l'Amérique du sud, 4-colorié.
Une 4-coloration, c'est la coloration des sommets d'un graphe avec 4 couleurs au plus de telles manières que deux sommets adjacents ne soient jamais de la même couleur.
Montrer que tout graphe planaire est 4-colorable n'est pas évident, mais montrer leur 6-colorabilité est facile, en procédant par récurrence. Si le graphe a moins de 6 sommets, aucune question ne se pose. Si il a plus de 6 sommets, la formule d'Euler implique l'existence d'un sommet de degré au plus 5 (avec au plus 5 voisins). On l'enlève, on applique la récurrence, on le remet, et on le colorie avec une couleur qui n'est pas dans son voisinage.
Au plus cinq couleurs...
25 ans plus tard, le problème de Guthrie a fait le tour du monde, et aucune démonstration n'est encore connue. Jusqu'à ce jour de juin 1879 où Alfre Kempe annonce au monde entier avoir démonté la conjecture des quatre couleurs, qui devient théorème. Tous les honneurs lui sont accordés, il est même nommé trésorier de la Royal Society (l'Académie des Sciences anglaise). Mais le bonheur sera de courte durée, puisqu'en 1890, Percy Heawood découvre une erreur dans la démonstration de Kempe, le genre d'erreur irréparable qui font retourner le problème des quatre couleurs au statut de conjecture. Heawood reprend alors tout le travail de Kempe, et parvient non pas à démontrer le théorème des 4 couleurs, mais le théorème des 5 couleurs. C'est déjà pas mal. La preuve du théorème de Heawood est plus longue que celle du théorème des 6 couleurs, mais elle garde le même esprit, avec l'utilisation de la formule d'Euler.
Bien que fausse, la preuve de Kempe reste tout de même intéressante, et suit l'idée du théorème des 6 couleurs. On choisit un sommet de degré 5. Dans les bons cas, la récurrence permet de conclure, sinon, on s'arrange.
En 1896, Charles-Jean Étienne Gustave Nicolas le Vieux Baron de la Vallée Poussin (mathématicien célèbre pour un théorème en théorie des nombres) découvre lui aussi l'erreur dans le travail de Kempe. Mais bon, il avait 6 ans de retard. Heawood passera le reste de sa vie à essayer de démontrer en vain le théorème des quatre couleurs...
Les travaux qui suivront monteront la validité sur les carte possédant au plus 24 pays, puis 27, 31, et jusqu'à 96 avant 1976.
Au plus quatre couleurs !
Nouveau siècle, nouveaux outils. En 1976, deux américains, Appel et Haken, annoncent avoir résolu le problème. Pour la deuxième et dernière fois, la conjecture deviendra théorème. Mais il y a un hic : pour la première fois dans une démonstration mathématique, ce n'est pas l'homme qui a le plus bossé, mais l'ordinateur... La démonstration tant attendue depuis plus d'un siècle est complètement décevante !
Pour ça, Appel et Haken ont à nouveau repris l'idée de démonstration de Kempe, mais en changeant un point important : au lieu de faire la récurrence en enlevant un seul sommet, ils ont procédé en enlevant plusieurs sommets, des "configurations". Ces configurations sont des plus petits graphes que l'on retrouve dans n'importe quel graphe planaire assez grand, et il n'y a qu'un nombre fini de configurations possibles : 1476... Recenser tous les cas possibles est un travail, vous vous en doutez, particulièrement rébarbatif. Et pourtant, ils l'ont fait à la main !
Par récurrence, on peut 4-colorier le graphe sans la configuration. Il ne reste plus qu'à montrer que le 4-coloriage peut toujours s'étendre à la configuration. Pour ça, il faut, pour chaque 4-coloriage de chaque combinaison, montrer que le prolongement est possible. Pour chaque configuration, il y a plusieurs milliers de coloriages à considérer, un par un. Même avec beaucoup de volonté, ce travail est hors de porté pour Appel et Haken, qui ont utilisé l'outil informatique pour le faire à leur place.
Plus tard, une autre équipe de mathématiciens parvient à réduire à 633 le nombre de configurations à considérer, mais l'ordinateur reste indispensable pour arriver au bout de la preuve.
Bref, l'ordinateur a torché un problème qui s'annonçait au départ très subtil : si on bloquait pour passer de 5 à 4 couleurs, c'est que les graphes planaires devaient avoir une subtilité jusqu'alors inconnue. Et quand un problème est subtil, la quête de la démonstration entraîne l'apparition de concepts novateurs. On peut penser au grand théorème de Fermat, dont la démonstration n'est qu'anecdotique comparé a ce qui en a germé.
Finalement, le problème des quatre couleurs était un problème dur, et sa démonstration bourrine n'utilise pas de concepts plus compliqués que ceux utilisés pour la démonstration du théorème des 5 couleurs.
Deuxième problème : une démonstration assistée par ordinateur est-elle quelque chose de légitime ? Le problème de la validité du théorème est renvoyé à celui de la validité du programme qui l'a engendré. Depuis 76, d'autres théorème ont été démontré avec l'outil informatique, notamment la conjecture de Kepler sur l'empilement des oranges.
En 2004, Georges Gonthier fera la une des revues scientifiques en annonçant une bonne fois pour toute que, oui, le théorème des 4 couleurs EST un théorème. Pour cela, il a soumis la preuve du théorème au logiciel Coq, qui l'a validé. Coq est un de ces logiciels qui peut vérifier pas à pas la validité d'une démonstration rédigé dans un langage qu'il peut comprendre. Coq a d'ailleurs vérifié que son propre code source n'est pas bugué !
Le vieux débat "pour ou contre les démonstrations par ordinateur" est toujours quelque chose de polémique. Cela dit, au point où on en est aujourd'hui, un logiciel d'assistant de preuve sera toujours au moins aussi sûr qu'une relecture même attentive d'une longue démonstration d'une centaine de pages...
Au plus partie entière de sept plus racine carrée de quarante-neuf moins vingt-quatre chi sur deux couleurs...
Revenons à Heawood. Il n'a peut être pas réussi à montrer le théorème pour des cartes dessinées sur le plan ou sur une sphère, mais il a quand même réussi à formuler une conjecture un plus fine qui dit ceci (aujourd'hui démontrée) :
Si une carte est dessiné sur une surface bornée dont la caractéristique d'Euler est χ, alors on peut la colorier en utilisant au plus
![]()
couleurs. ⎣x⎦ représente la partie entière de x. La caractéristique d'Euler χ d'une surface, c'est le nombre que l'on trouve avec la formule S-A+F lorsque l'on y dessine un graphe. Par exemple, la caractéristique d'Euler du plan ou de la sphère, c'est χ=2. Pour un tore, un ruban de Möbius ou une bouteille de Klein, on trouve χ=0 (et donc, N=7). Pour un tore à g trous, on a χ=2-2g. Ce théorème donne un nombre suffisant de couleurs : on pourrait démontrer que dans le cas du ruban de Möbius ou de la bouteille de Klein, 6 couleurs suffisent.
Autrement dit : une carte dessinée sur un tore (un Donut's) peut toujours être coloriée en utilisant au plus 7 couleurs. La preuve en image : sur ce patron de tore, chaque pays touche les 6 autres pays, 7 couleurs sont donc nécessaires.
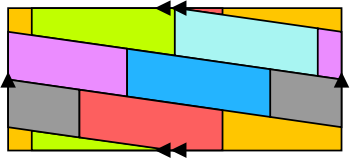
Pour obtenir un tore, il faut recoller les faces opposées en suivant le sens des flèches, ce qui donne cela.
Bref, le théorème des 4 couleurs continue de garder ses secrets. Une démonstration de quelques pages doit sûrement exister, quelque part dans les décimales de pi...
Sources :
The four colour theorem, par J J O'Connor and E F Robertson
La vérité et la machine, Par Benjamen Werner sur interstice



/https%3A%2F%2Fassets.over-blog.com%2Ft%2Fcedistic%2Fcamera.png)
/http%3A%2F%2Fstorage.canalblog.com%2F61%2F83%2F210892%2F87756146_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F92%2F62%2F210892%2F86697250_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F71%2F23%2F210892%2F57859833_o.png)