Espèce de brachistochrone !
Quel est le rapport entre une roue de vélo et un half-pipe, en skate-board ?
Le half-pipe idéal
La réponse est entre les deux points bleus : la courbe brachistochrone, qui ressemble (de loin, dans le brouillard) à un quart de roue de vélo.
Sous ce nom bizarre se cache LA courbe de la fin du XVIIe siècle, sur laquelle les meilleurs mathématiciens de l'époque se sont tirés la bourre : Bernoulli (Jean, formateur du jeune Euler), Newton (Isaac, l'inventeur du calcul différentiel), Leibniz (Gottfried, l'inventeur du calcul différentiel, mais mais au même endroit), L'Hôpital ("Guillaume François Antoine de ~, marquis de Sainte-Mesme, comte d'Entremont, seigneur d'Oucques, La Chaise, Le Bréau et autres lieux", à qui l'on doit la règle de l'Hôpital) , Bernoulli (Jacques, qui a donné son nom à la loi de Bernoulli, le frère rival de Jean)...
Revenons donc à Bernoulli,
Il posait la question ainsi (en 1696, en latin, et pas vraiment de cette façon là) :
Étant donné deux points A et B dans un plan vertical, quelle courbe reliant les deux points permet à une bille posée en A de rejoindre B en en minimum de temps ?
Cette courbe a été appelée courbe brachistochrone (du grec brakhisto « le plus court » et de chronos « temps ») par Jean Bernoulli.
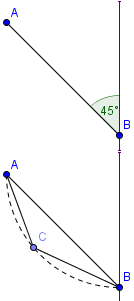Galilée avait déjà donné sa réponse 60 ans plus tôt. Pour lui, c'est l'arc de cercle qui permet de relier le plus rapidement les deux points. Les frères Bernoulli ne lui donneront pas raison !
Galilée ne s'était pas posé initialement le problème de la courbe brachistochrone mais de la droite brachistochrone : comment aller au plus vite d'un point A jusqu'à une droite verticale donnée (au point B) ? Galilée trouva assez rapidement la réponse : il faut que cette droite forme un angle de 45° avec la verticale donnée.
Il ne s'arrêta pas en si bon chemin, et remarqua que si on ajoute un point C sur l'arc de cercle AB, alors le chemin [AB][BC] sera encore plus rapide. Il en conclu que l'arc de cercle devait être le chemin le plus rapide entre les deux points !
Revenons donc à Bernoulli
Ayant déjà résolu la question, il proposa à ses collègues mathématiciens d'essayer également de déterminer quelle est la courbe brachistochrone. Le challenge était de trouver la réponse en mois de 6 mois.
Finalement, Jean Bernoulli accepta, à la demande de Leibniz, de reculer la date. Au final, 5 mathématicien ont donné une réponse : Newton, Bernoulli (Jacques), Leibniz, L'Hôpital et Bernoulli (Jean).
Et cette réponse, quelle est-elle ?
La réponse se trouve sur la roue d'un vélo : la cycloïde. En imaginant un vélo qui roule, la cycloïde est la trajectoire d'un point situé sur le pneu de la roue, vu depuis la route.
Cycloïde, tracée par un cercle roulant sur le sol.
Ainsi, pour aller au plus vite du point A au point B, il suffit de se placer sur un arc de cycloïde renversé, en partant de l'un de ses sommet (on commence alors avec une tangente verticale).
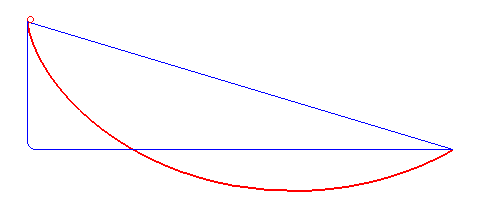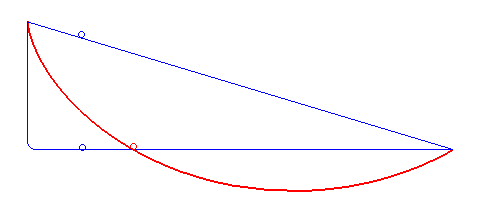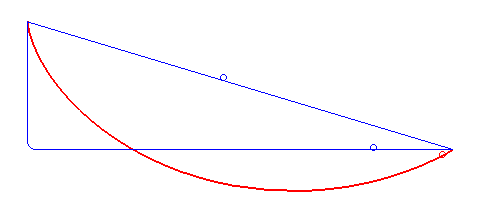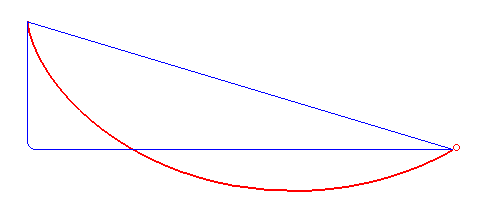
La cycloïde, en rouge
Et c'est à ce moment là que les choses deviennent surprenante : la courbe possède une portion qui remonte ! Le chemin le plus rapide n'est décidément pas le plus court, loin de là !
Revenons-donc à Bernoulli
En fait, la question que Bernoulli a posé n'était pas vraiment celle là, mais était plus proche de la question de Galilée : quelle est la courbe brachistochrone entre un point A donné et une verticale ?
Autrement dit, quelle est la plus rapide de toutes les cycloïdes ayant un somment en A ?
Cette fois-ci, la réponse est un peu plus intuitive : parmi toutes les cycloïdes, la meilleure est celle qui terminant horizontalement.
La courbe brachistochrone : un demi-arc de cycloïde, commençant verticalement, terminant horizontalement.
Le dénivelé entre le départ et l'arrivée est de 2/π (pour une distance entre A et la verticale de 1)
La cycloïde renversée ne se contente pas d'être brachistochrone : elle est également tautochrone (deux billes placée à des points différents du demi-arc arriveront en même temps en bas, à une vitesse différente), et même isochrone (une bille placée dans l'arc oscillera, avec une fréquence indépendante de la position initiale).
A noter que la courbe cycloïde a été nommée et étudiée par Galilée, qui n'a pas pensé à la replacer dans le cadre de son problème brachistochrone...
Sources :
Historique et démonstrations de ce problème (en anglais)
/http%3A%2F%2Fstorage.canalblog.com%2F68%2F79%2F210892%2F119772528_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F43%2F63%2F210892%2F119161093_o.gif)
/http%3A%2F%2Fstorage.canalblog.com%2F74%2F79%2F210892%2F116430959_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F50%2F97%2F210892%2F91694671_o.png)