... et intégrale curviligne !
Le 15 novembre 2006, un séisme ravageait les côtes des îles Kouriles, Al-Jezira lançait son bouquet satellite, le gouvernement validait les conditions d'application d'interdiction de fumer dans les lieux public... Mais surtout, le blog Choux Romanesco, vache qui rit et intégrales curvilignes poussait son premier cri !
Après 170 messages/notes/articles/billets, c'est donc aujourd'hui que mon petit blog fête son troisième anniversaire ! Tout un panel de star est même venu célébrer avec nous cet évènement !
Donc, quel sujet aborder pour ce troisième anniversaire ?
J'aurai pu continuer dans la logique de mes notes du moment, et passer aux nombres hypercomplexes... Non, je garde ça pour la semaine prochaine.
J'aurai pu suivre l'actu et parler du vendredi 13 (comme on me l'a suggéré par e-mail)... Non, ça sera pour août 2010 ! (En espérant secrètement que j'aurai réussi à tenir le blog jusqu'à là)
Aujourd'hui, je vais plutôt tenter de répondre à cette grande question : "Intégrale curviquoi ?", en tentant une petite initiation à l'analyse vectorielle (promis, je ne recommencerai pas dans l'année à venir !)...
Intégrale ...
A l'origine, ce que l'on appelle "intégrale" (entre a et b de la fonction f) représente "l'aire sous la courbe" de la fonction f (supposée positive) entre le point a et le point b, que l'on note à l'aide du symbole ∫ (qui représente une notion de somme) et de son "dx". Si la fonction était négative, on compterai cette aire négativement. Quand on calcule cette aire, on dit que l'on "intègre" la fonction f entre a et b (ou qu'on la "quarre", pour parler à l'ancienne).
Trouver "l'aire sous la courbe", c'est sympa 5 minutes, mais on en est venu très vite à généraliser :
- intégrale généralisée (ou impropres) : au lieu de rester sur un intervalle [a,b] (de longueur finie), intégrer la fonction sur ℝ tout entier ! Ça apporte tout un tas de problèmes de convergence dont on se serait bien passé, mais c'est pour ça qu'on les aime !
- intégrale double : au lieu de calculer "l'aire sous la courbe" sur un segment [a,b], on pourrait généraliser à la dimension supérieure en calculant le "volume sous la surface" sur un domaine K (une zone délimitée du plan). On notera "le volume sous la surface z=f(x,y)" par ∫∫Kf(x,y)dxdy. Dans le cas où f est la fonction constante (f(x,y)=1), on peut se dire que l'intégrale multiple ∫∫K dxdy représente en fait l'aire du domaine K.
- intégrale multiple : on peut évidemment généraliser les intégrales double aux espaces de dimensions supérieures, et définir "l'hypervolume sous l'hypersurface"... On peut même faire des intégrales généralisées multiples ! Évidemment, c'est plus abstrait...
- intégrale curviligne d'un champ scalaire : ces intégrales permettent de définir "l'aire au dessus d'une courbe et sous une surface". On se place dans l'espace. On considère une courbe γ du plan Oxy, et une surface d'équation z=f(x,y). L'intégrale curviligne ∫γ f ds désigne alors l'aire au dessus de la courbe et sous la surface.
Quand un problème demande de calculer des aires ou des volumes (autre que des rectangles ou des triangles, ou les formules sont bien connues), on ne peut jamais échapper au calcul d'une intégrale... Le problème, c'est que dans la majorité des cas, le calcul d'une intégrale n'est jamais quelques chose de simple. Alors, comment mesurer une aire sans se fatiguer ?...
Intégrale curviligne d'un champs de vecteur
Dans la pratique, les intégrales curvilignes ne servent pas du tout à calculer des aires... Pour dire la vérité, les intégrales curviligne, c'est quand même un truc de physicien, qui s'en servent (entre autres) pour calculer le travail d'une force sur un chemin.
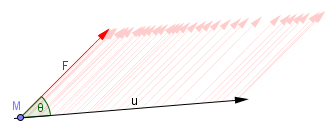
Le travail de la force F le long de u est donné par W=F.u=|F|.|u|.cos(θ)
En Terminale S, on découvre avec stupeur que pour calculer le travail W d'une force F constante sur un trajet rectiligne u, il fallait prendre le produit scalaire entre F et u.
Mais sur un mouvement, la force qui s'applique au mobile n'est pas forcément constante, et la trajectoire n'est pas forcément rectiligne. Qu'à cela ne tienne ! Quant le mobile ne bouge qu'un petit peu, le bout de courbe peut-être assimilée à un bout de droite (du), et la force peut être vue comme constante. Sur ce petit mouvement, la force produit un travail élémentaire, noté δW.
En chaque point, la force exercée sur M est différente
En sommant tous les travaux élémentaires, on trouve le travail total de la force : W=∫γ F du. C'est l'intégrale curviligne de F le long du chemin γ (aussi appelé "circulation") !
F, ici, représente un vecteur ℝ², et il dépend du point M (dans R²). On peut donc voir F comme une fonction de ℝ² dans ℝ². On a en fait F=(P(x,y),Q(x,y)). On peut alors écrire l'intégrale curviligne sous la forme ∫γ F du.=∫γ P dx+ Q dy.
Et c'est là que la magie opère, avec le théorème de Green-Riemann, qui permet de relier l'intégrale curviligne d'une courbe fermée (où le point d'arrivée correspond à celui du départ, ce qui délimite un domaine du plan) avec une intégrale double sur ce domaine ("le volume sous la surface" ou même, dans certaines conditions, l'aire du domaine). En gros, on peut connaître l'aire d'un domaine du plan seulement en parcourant sa frontière !
[En notant K un domaine du plan et δK sa frontière, le théorème de Green Riemann nous dit que l'on a l'égalité :
∫δK Pdx+Qdy = ∫∫K [δxQ-δyP]dxdy
où δxQ désigne la dérivée de Q par rapport à sa première variable, et δyP désigne la dérivée de P par rapport à sa deuxième variable.
Les gens observateurs verront que prendre Q=x et P=0 permet d'obtenir l'aire du domaine K]
Le planimètre polaire
Le plus étrange dans toute cette théorie, c'est qu'on puisse si facilement lui trouver une utilité ! A la fin du XIXe siècle, l'ingénieur suisse Jakob Amsler-Laffon a eu l'idée d'utiliser ce théorème pour quarrer mécaniquement les courbes : il a construit le premier planimètre polaire, objet qui, à l'instar de la règle pour mesurer les longueurs, permet de mesurer facilement les aires. Puisque l'on peut obtenir l'aire délimitée par une courbe seulement en marchant le long de la courbe (par Green-Riemann), Amsler s'est dit, à raison, qu'il devait être possible de le fabriquer mécanique !
Schématiquement, le résultat ressemble à ceci :
Le planimètre se présente sous la forme de deux bras T-S articulés en A, où le point O est fixe. En N se trouve une roue d'axe S, et en M se trouve le curseur. Lorsque celui-ci se déplace le long de la courbe, la roue va intégrer les vecteurs en verts.
Lorsque l'on déplace la tête M le long de la courbe à quarrer, la roue située en N tourne sur son axe. Elle ne tourne pas lorsque la tête se déplace dans la direction de S, et tourne d'autant plus vite que le chemin de M est perpendiculaire à S.
Lorsque le point M a fait le tour la courbe, on peut connaître l'aire de la courbe en regardant le nombre de tours de la roue, puisque celui-ci est proportionnel à l'aire de la courbe (ça ne se trouve pas comme ça, ya quelques calculs malin derrière !). En l'étalonnant sur un carré de 1cm², cet instrument permet de quarrer sans se fatiguer les domaines les plus étriqués !
A la semaine prochaine, pour l'article qui célèbrera les 3 ans et une semaine du blog !
N'empêche, vous en connaissez beaucoup des blogs sur lequel on peut trouver à la fois Britney Spears et un théorème d'analyse vectorielle ?...
Sources :
Intégrale curviligne, cours de P. Pansu
Le planimètre polaire, de B. Aebischer
Et le site gnomz pour les messages auto-promotionnels VIP
/https%3A%2F%2Fassets.over-blog.com%2Ft%2Fcedistic%2Fcamera.png)
/http%3A%2F%2Fstorage.canalblog.com%2F61%2F83%2F210892%2F87756146_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F92%2F62%2F210892%2F86697250_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F23%2F05%2F210892%2F58955538_o.png)