Plus de carrés, plus de magie, plus de champagne

Non, j'en ai pas fini avec les carrés magiques ! La semaine dernière, nous en explorions sur ce blog la partie émergée avec les carrés multimagiques. Cette semaine, je vous propose de continuer l'exploration de la jungle des carrés magiques, dans le but non avoué d'avoir un lecteur futur détenteur d'une bouteille de champagne aux extraits naturels de carrés magiques.

Faut-il encore le rappeler (oui...) : un carré magique d'ordre n est un tableau carré n×n de nombres disposés de telle manière que leur somme sur chaque rangée, colonne et diagonale soit égale. On demande généralement à ce qu'aucun nombre ne soit représenté plusieurs fois dans le carré (sinon, c'est trop facile)

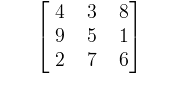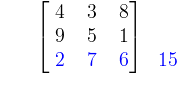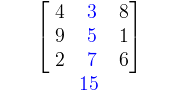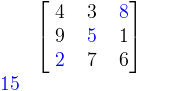
Carré magique d'ordre 3

Un carré magique est forcément d'ordre au moins 3, mais il en existe pour n'importe quel ordre plus grand (même si, a priori, on ne sait pas en construire pour un nombre donné quelconque).
Le 6 avril dernier, Christian Boyer a lancé un communiqué de presse mettant à prix la résolution des problèmes des plus petits carrés magiques possibles répondant à certaines contraintes. 12 énigmes sont proposées, chacune doté d'un prix d'une bouteille de champagne et d'un chèque de 1000€ ou 500€.

Énigme 2 : Construire (ou prouver l'impossibilité de construire) un carré bi-magique d'ordre 5
Mise à prix : 1000€ et une bouteille de champagne
Tous les détails là-bas.

Énigme 1 : Améliorer (ou prouver l'impossibilité d'améliorer) le record de carré magique de carrés d'ordre 3
Mise à prix : 1000€ et une bouteille de champagne
Un carré bi-magique est un carré magique qui reste magique quand on élève tous ses éléments au carré. On sait depuis 1891 (et 2004) qu'il n'en existe pas de tels d'ordre 3 (et 4). Mais pour les carrés magiques composés seulement de nombres entiers au carré, la question ne se résout pas si facilement !

Ce problème débute avec Leonhard Euler qui envoie en 1770 un carré magique à Joseph Lagrange. C'est un carré magique d'ordre 4 construit seulement avec des nombres carrés. Dans sa quête de démontrer ce qui sera le théorème des 4 carrés de Lagrange ("Tout entier peut s'écrire comme somme de 4 carrés"), le bougre avait en fait trouvé une façon plus générale de fabriquer des carrés magiques de carrés d'ordre 4 (demandant 8 paramètres).

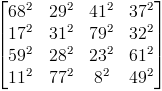
Carré magique de carrés de Euler, de constante magique 8515

La méthode d'Euler permet de trouver un carré magique avec une constante plus petite (2004) :

Carré magique de carrés de constante magique 3230

En existe-t-il pour des ordres différents ? Il faudra attendre 1890 pour obtenir une réponse positive : G. Pfeffermann montre qu'il existe de tels carrés magiques pour des ordres 8 et 9 (il trouve en fait des carrés bimagiques). Reste donc à en trouver pour les ordres 3, 5, 6 et 7... Ca sera en juin 2005 que le problème sera presque résolu, puisque Christian Boyer découvre l'existence de carrés magiques de carrés d'ordre 5, 6 et 7. Le problème pour l'ordre 3 est donc toujours présent !

En 1996, Martin Gardner pose explicitement le problème de l'existence d'un carré magique de carrés d'ordre 3. Pour encourager les recherches, il propose 100$ de sa poche à celui qui trouvera une solution. Le problème peut s'appréhender de deux façons différentes : essayer de maximiser le nombre de carrés ou essayer de maximiser le nombre de lignes/colonnes/diagonales justes.

Carré magique possédant 7 nombres carrés sur 9, de l'américain Andrew Bremner (1997), de constante magique 541 875

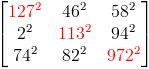
Carré presque magique, du hollandais Lee Sallows (1996), de constante magique 147². Seule la première diagonale ne donne pas le bon résultat.

On a réussi depuis à créer bien pire dans les carrés magiques de la forme de celui de Sallows. On a notamment un résultat tout à fait impressionnant de Frank Rubin, où la première diagonale persiste à ne pas donner la bonne somme, mais le rapport entre la constante magique (43474203911235768609981537098048163²) et la somme sur la première diagonale est de 1.0000000000000000705...

(Cliquer pour voir en plus grand)

Quelqu'un pour faire mieux ? Il faudrait trouver un carré magique avec au moins 7 carrés non trivialement différents de celui de Bremner (prendre le même carré en multipliant tous les éléments par 4 ne sera pas toléré), ou encore mieux s'il possède 8 ou 9 carrés ! Boyer proposait en 2005 la somme de 100€ pour celui qui fera mieux, mais a décuplé la prime en avril dernier !

Les récentes recherches dans la question ont amené à penser que si il existe un carré magique de carré d'ordre 3, alors ses éléments sont au moins supérieurs à 10¹⁴...

Énigme 4 : Construire (ou prouver l'impossibilité de construire) un carré magique de cubes d'ordre 4, 5, 6 ou 7
Mise à prix :
* 1000€ et une bouteille de champagne (ordre 4)
* 500€ et une bouteille de champagne (ordre 5)
* 500€ et une bouteille de champagne (ordre 6)
* 200€ et une bouteille de champagne (ordre 7)

Quand on se pose la question pour les carrés, on se la pose forcément pour les cubes : peut-on construire des carrés magiques composés seulement de cubes ? Et de puissances supérieures ?

On peut déjà répondre à la deuxième partie de la question dans le cas de l'ordre 3: un tel carré magique ne peut être composé seulement de nombres élevés à la puissance n dès que n≥4. L'existence d'un tel carré magique demande l'existence de nombres entiers x,y z vérifiant xⁿ+yⁿ=2zⁿ (le centre d'un carré magique d'ordre 3 est égale au tiers de la constante magique)
Le cas n=4 se déduit d'un résultat de Legendre (qui dit qu'il n'y a pas de solutions entières non triviales à l'équation x⁴+y⁴=2z²), et le cas général se déduit d'un corollaire du dernier théorème de Fermat.
Bref : rien n'interdit l'existence d'un carré magique de cubes d'ordre 3 !

Le premier carré magique de cette forme est découvert en 2006 par Boyer : c'est un carré d'ordre 9. Le résultat sera battu en 2008 par l'allemand Walter Trump, qui en trouve un d'ordre 8 :

Carré magique de cubes de W. Trump, de constante magique 636 363. Tous les entiers de 1 à 68 sont utilisés, sauf 17, 28, 44 et 67.

Depuis, impossible de faire mieux...

Énigme 3 : Construire (ou prouver l'impossibilité de construire) un carré semi-magique de cubes d'ordre 3 ou 7
Mise à prix :
* 1000€ et une bouteille de champagne (ordre 3)
* 100€ et une bouteille de champagne (ordre 7)

On parle de carré semi-magique quand les diagonales du carré magique ne donnent pas la constante magique. On connaît des carrés semi-magiques de carrés et de cubes pour à peu près tous les ordres (Connus depuis 2006). Seuls deux d'entre eux posent problème : les carrés semi-magiques de cubes d'ordre 3 et d'ordre 7...

Énigme 6 : Construire (ou prouver l'impossibilité de construire) un carré magique additif et multiplicatif d'ordre 5, 6 ou 7
Mise à prix :
* 1000€ et une bouteille de champagne (ordre 5)
* 500€ et une bouteille de champagne (ordre 6)
* 100€ et une bouteille de champagne (ordre 7)

Dans un carré magique, la somme sur les lignes, colonnes ou diagonales est toujours la même : il est dit additif. Mais si au lieu de s'intéresser à la somme, on s'intéresse au produit ? On parle alors de carré magique multiplicatif quand le produit sur les ligne, colonnes et diagonales est constant.
Un carré magique est additif et multiplicatif s'il est à la fois additif... et multiplicatif !

Une manière facile pour construire un carré magique multiplicatif est de partir d'un carré magique additif, et de prendre l'exponentielle de chaque élément. Par exemple, en partant du carré magique du début de l'article, on trouve le carré magique multiplicatif suivant :

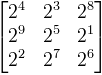
Carré magique multiplicatif, de constante magique 2^15

On peut aussi construire des carrés magiques multiplicatifs qui ne sont pas de la forme précédente. L'exemple suivant date de 1917, et est dû à l'anglais Henry Dudeney :

Carrés magiques multiplicatifs de Dudeney, de constante magique a³b³

Mais dès qu'il s'agit de carrés magiques à la fois additifs et multiplicatifs, les choses se corsent vraiment ! Les premiers exemples datent des années 50, et sont signés de l'américain Walter Horner. Ils sont d'ordre 9 (1952) et 8 (1955). La bête de concours de Horner ressemble à ça :

Carré magique additif et multiplicatif, de constantes magiques 840 et 2 058 068 231 856 000.

Ce record est optimisable (en 2005, de tels carrés magiques ont été découvert avec des nombres plus petits ou des constantes magiques plus petits), mais restent désespérément d'ordre 8.

En 2007, l'américain Lee Morgenstern s'empare du problème, et avance dans la compréhension du problème : les carrés magiques add-mult d'ordre 3 et 4 sont démontrés impossibles, et des carrés semi-magiques add-mult d'ordre 4, 5 et 6 seront construits. Les incertitudes restent alors sur les carrés semi-magiques add-mult d'ordre 7 (qui ne fait l'objet d'aucune récompense), et sur les carrés magiques add-mult d'ordre 5, 6 et 7.

Pour les ordres plus grand, de nombreux carrés magiques add-mult ont été découverts. Entre l'ordre 8 et 32, aucun n'ont été découvert pour les ordres 11, 13, 17, 19, 22, 23, 26, 29 et 31 (en gros, les nombres premiers et leur doubles). Ces problèmes n'ont pas été mis à prix, mais seront récompensés par des étoiles dans les yeux de Christian Boyer !
Pour le fun, un carré magique additif et multiplicatif d'ordre 1024 a été construit, pour montrer qu'il en existe bien de très grands !

Énigme 5 : Améliorer (ou prouver l'impossibilité d'améliorer) le record du plus petit cube magique multiplicatif
Mise à prix :
* 1000€ et une bouteille de champagne

Il n'y a pas que les carrés qui sont magiques, les cubes peuvent tout à fait l'être aussi ! Il faut pour cela que la somme sur les n² lignes, n² colonnes, n² piles et 4 triagonales du cube soit constante. Quand on demande à ce que les 6n diagonales donnent également la constante magique, on parle de cube magique parfait. Les cubes magiques parfaits d'ordre 3 et 4 ont été démontrés impossibles, et des cubes d'ordre 5 et 6 ont été publiés en 2003 (Boyer & Trump) : le problème des plus petits cubes parfaits n'est plus vraiment à l'ordre du jour.

Cube magique parfait de Trump et Boyer : c'est le plus petit possible ! Il contient tous les entiers de 1 à 125, sa constante magique est donc 315

L'énigme ici porte cependant sur les cubes magiques multiplicatifs (pas forcément parfaits) : le record est à un cube d'ordre 4 et de coefficient maximal 364. Pour résoudre l'énigme, il faut en trouver un avec des coefficients tous plus petits que 364, d'ordre quelconque (entre 3 et 7, tout de même). Le cube le plus petit connu est d'ordre 3, mais son coefficient maximal est 400... Il semble impossible de faire mieux que 364, avec ce cube-ci, signé Boyer :

Pour ce qui est des cubes magiques multiplicatifs parfaits, la méthode consistant à prendre un cube magique additif parfait, et à remplacer les éléments par les constantes marche... mais n'est pas vraiment recommandée, vu la taille des éléments que la méthode engendre. Le record dans la catégorie cube magique multiplicatif parfait est à l'ordre 7, avec des coefficients tous plus petits que 1 259 712.

Pendant ce temps là, au Japon
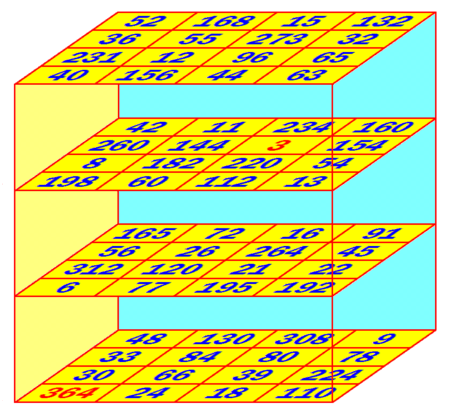
Entre le moment où je souhaite rédiger un article et le moment où celui-ci est finalement paru, de très longues semaines peuvent passer... L'actualité m'a rapidement dépassé : 2 des récompenses sont déjà tombées ! Le japonais Toshihiro Shirakawa repart donc avec deux bouteilles de champagne et 1100€, puisqu'il a donné un exemple de cube magique multiplicatif de plus grand terme 351 (15 avril 2010), et un carré semi-magique d'ordre 7 (22 avril 2010) :

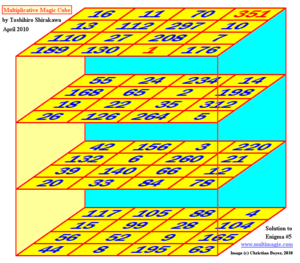
Le cube magique objet de tous les désirs (1000€)

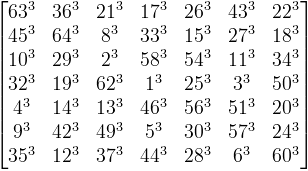
Et le carré semi-magique objet d'un peu moins de désirs  (100€)

Allez, plus que 10 systèmes d'équations diophantiennes à au moins 10 inconnues à résoudre... Bon courage !

---

Sources :
Multimagie.com : le site de référence sur les carrés multimagiques, par Christian Boyer, d'où proviennent les illustrations des cubes (que j'ai eu la flemme de réécrire)
Avec le communiqué de presse du 6 avril 2010 mettant à prix ces problèmes

<