Un peu de topologie algébrique pour tout le monde

Comment transformer des considérations du genre "SO(3) n'est pas simplement connexe" de la théorie des groupes fondamentaux de la topologie algébrique en de merveilleux tours de magie pour étonner petits et grands pour les fêtes de fin d'année ? Aujourd'hui, Chouxrom'co vous propose deux énigmes topologiques, qui peuvent très facilement se transformer en tours de magie quand on donne la réponse en y ajoutant un brin de théâtralité.
Par manque de temps, l'article d'aujourd'hui ressemblera beaucoup à deux billets postés chez Math O' Man et Pierre Bernard.

Comment mal accrocher un cadre à son mur ?
Attention, énigme topologique ! (à poser au réveillon pour faire réfléchir belle-maman).
Vous venez d'acquérir une reproduction du Déjeuner sur l'herbe de Claude Monet, et souhaitez l'accrocher au mur de votre salon. Sur ce mur, deux clous sont déjà plantés, et un fil relie les deux coins du tableau. Pour rigoler, vous voulez faire en sorte que lorsque l'un des deux clous (n'importe lequel) est retiré, le tableau tombe. Comment procéder ? Ce problème répond au nom de "porte-manteau de Paolo", du nom de Paolo Bellingeri, mathématicien à l'Université de Caen.

Question subsidiaire : généraliser à 3 clous, à n clous...

Torsion et physique quantique
Attention : énigme topologique ! (à poser à la Saint-Sylvestre pour faire réfléchir tonton Jean)
Pour cette énigme, vous avez besoin d'un petit bout de carton et de quatre élastiques. Réalisez alors le montage suivant :

Au milieu, le bout de carton (ou n'importe quoi d'autre), fixé par quatre élastiques.

Faites faire alors deux tours à votre bout de carton, ce qui doit donner quelque chose comme ça :

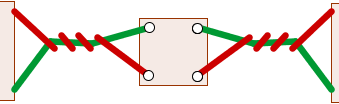
Les élastiques paraissent emmêlés, et pourtant, on peut les démêler sans toucher aux supports, ni retourner le carton dans l'autre sens....Comment faire ? Et pourquoi deux tours et pas un seul ?

Comment mal accrocher un cadre à son mur ? Partie II
Attention, solution topologique !

Sans plus attendre, voici en image une solution de ce problème qui vous tient en haleine depuis une bonne minute :

Une solution (a.b.a^-1.b^-1) du problème : le tableau est accroché aux clous (figurés par des gros points bleus), mais lorsque l'on retire l'un d'entre eux, il se casse la gueule.

Mais c'est pas parce qu'on a la solution que l'on comprend ce qui se trame derrière ce dispositif. Pour ça, il va falloir s'intéresser au monde de la topologie algébrique qui dit que "le groupe fondamental de ℝ²-{a,b} est isomorphe au groupe libre à deux générateurs"...

Intéressons-nous plutôt aux faits, et regardons le premier clou A. Il y a deux façons d'enrouler la ficelle : dans le sens des aiguilles d'une montre (on note ça a) ou dans l'autre sens (a^-1). De même avec le clou B : le sens b ou le sens b^-1.

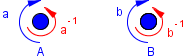
Accrocher le cadre, c'est juste dire dans quel ordre et dans quel sens il faut enrouler la ficelle. Dans la solution, on commence par tourner autour du premier clou dans le sens des aiguilles d'une montre (a), puis autour du deuxième (b), on revient dans l'autre sens autour du premier (a^-1), puis dans le même sens autour du deuxième (b^-1). On note ce chemin a.b.a^-1.b^-1 (noté aussi [a,b]). Le point signifie ici "suivi de".

Deuxième chose à comprendre, c'est que enrouler la ficelle autour du clou dans un sens (a) puis dans l'autre (a^-1), c'est comme ne rien enrouler du tout (l'enroulement nul est noté 1) : a.a^-1=1. On trouve d'autre relations algébriques simples sur les enroulements, comme a.a^-1=a^-1.a=1 et a.1=1.a=a.
Enfin, supprimer un clou, c'est faire comme si on avait jamais rien enroulé autour. Retirer le clou B, c'est transformer en 1 les occurrences b et b^-1 dans le chemin.

Ainsi, quand on retire le clou B du chemin a.b.a^-1.b^-1, on trouve a.1.a^-1.1=a.a^-1=1 : l'enroulement que l'on obtient une fois le clou B retiré est l'enroulement nul, ce qui signifie que le cadre n'est plus retenu.

Et pour généraliser à trois clous ou plus, il suffit de construire les enroulements à l'aide des commutateurs. Par exemple, pour 3 clous, on peut utiliser le chemin [a,[b,c]] = a.b.c.b^-1.c^-1.a^-1.c.b.c^-1.b^-1. Cette construction se généralise facilement à 42 clous, même si le dispositif devient difficile à réaliser dans la réalité.

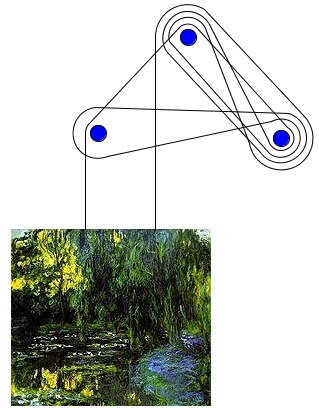
Je ne préfère pas essayer de dessiner le dispositif avec 4 clous...

Torsion et physique quantique, partie II
Ce problème/tour de magie illustre le fait que dans l'espace (à 3 dimensions ou plus), faire deux tours, c'est comme ne pas faire de tour du tout (alors que faire un seul tour, c'est faire un tour).  L'expérience du carton et des élastiques date de 1981 (décrite par René Deheuvels dans Formes quadratiques et groupes classiques), mais une autre illustration de ce phénomène a été décrite par DavidL dans les commentaires du dernier article :

Posez un objet dans votre main, et faites-lui effectuer un tour à 360° (en le faisant passer sous votre bras) : l'objet en question revient dans sa position initiale, mais pas votre bras. Faites-lui faire à nouveau un tour à 360°, toujours dans le même sens (en faisant passer par-dessus votre épaule. Cette fois ci, votre bras et votre objet reviennent en position initiale.

Ce phénomène, que l'on observe ici à grande échelle, se retrouve à l'échelle des particule sous le nom de spin (si un expert en physique quantique est capable de vulgariser ce qu'il en retourne, qu'il se présente au plus vite).
Pour en revenir au problème initial, la solution est de faire disparaitre les torsions en faisant passer les boucles de part et d'autre du carton. Une animation vaut mieux que trop d'explications :

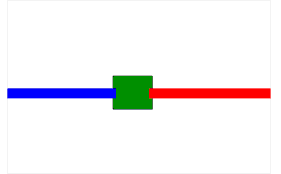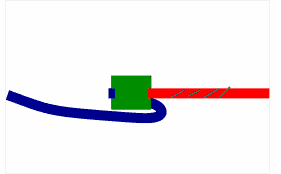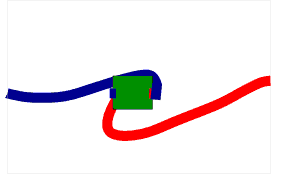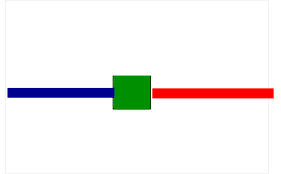
Animation récupérée sur Jeux et Mathématiques.

Bref : même si faire faire un tour au carton emmêle les fils, faire faire un deuxième tour les démêle, peu importe le sens. Topologiquement parlant, la rotation à 720° est équivalente à la non-rotation : on dit qu'elles sont homotopes.

Oui, mais pourquoi ? On appelle SO(3) l'ensemble des rotations de l'espace (qui sont déterminées par un axe orienté et un angle de [-180°,180°[). On peut se représenter géométriquement cet ensemble en regardant une boule de rayon 180.

A tout point x de cette boule correspond une rotation de l'espace : [Ox) donne l'axe de rotation, et la distance Ox donne l'angle de rotation. Seulement, deux points opposés de la sphère correspondent à la même rotation (un rotation de 180° dans un sens, c'est comme une rotation dans l'autre) : SO(3) correspond à la boule B3 où on a identifié les points antipodaux.

Faire faire un tour de 360° autour de l'axe (PQ), c'est prendre un chemin dans SO(3) qui part de la rotation nulle et qui va à la rotation de 360°, en passant par toutes les rotations intermédiaires. De manière équivalente, c'est partir de la rotation autour de (PQ) de 180° pour arriver à celle de -180°. Sur le dessin, c'est le chemin g qui part de P pour aller à Q en passant par O.

Ce chemin se déforme facilement en le chemin h qui part de P pour aller à Q en restant sur le bord de la boule (On passe de la rotation à son opposée en bougeant l'axe et non l'angle). Homotopiquement, g=h.

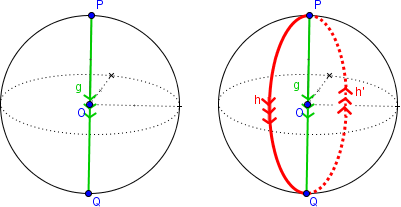
A gauche, le chemin g dans SO(3) qui correspond à un tour à 360°
A droite, les chemins h et h' qui correspondent également à des tours à 360°. Le chemin h.h' peut se rétracter sur le point P pour former un chemin nul.

Puisque les points de la sphère sont identifiés aux points opposés, le chemin h est le même que le chemin h' de l'autre côté. Le chemin h.h' peut se déformer jusqu'au point P, et donc, le chemin h.h' est homotopiquement équivalent au chemin nul. Bref : h.h'=1.
Faire faire un tour de 720°, c'est faire le chemin g.g. Par les différentes égalités qu'on a écrit, on en déduit que g.g=h.h'=1. Résumé : faire faire deux tours de 360°, c'est comme ne pas faire de tours du tout !

La dernière chose qu'il faudrait montrer, c'est que le tour de 360° dans l'espace n'est pas équivalent homotopiquement au non-tour. Mais c'est quand même un peu plus compliqué.

---

Sources :
Le blog de Math o' man
Le blog de Pierre Bernard
Le site Jeux et Mathématiques : spin.
Un topic sur l'expérience du spin, sur Les-mathematiques.net.
Deux autres illustrations du "deux tours = pas de tours", fournies par Byby dans les commentaires de l'article précédent : ici et là.

Comments

[thomascabaret]

Je considere avoir répondu à la question sur le spin. (Youtube Passe-science Le Spin) :P "Au plus vite" bon ok ca fait 9 ans.

[DavidL]

Content de voir que ma question du billet précédent t'a inspiré !
Pour le lien entre groupe et spin, je n'ai que de vagues souvenirs mais en gros quand on a un groupe qui peut opérer sur notre système 'classique' (ici le groupe des rotations SO(3)), et qu'on veut trouver le groupe correspondant qui va agir sur le système 'quantifié', il faut (je ne sais plus pourquoi) aller chercher le groupe de recouvrement universel, donc SU(2) pour SO(3).
Donc sur le système quantifié (la fonction d'onde) peuvent opérer des représentations de SU(2) qui ne sont pas des représentations de SO(3), typiquement les représentations de spin demi-entier.
Voilà pour ce qui me reste, si quelqu'un peut boucher les trous du raisonnement...

[MathOMan]

Belles explications et illustrations ! Petite erreur de frappe :
"c'est transformer les occurrences b et b-1 dans le chemin en 1."