Il existe 10 types de mathématiciens...
Ceux qui comprennent le binaire, ceux qui ne comprennent pas le binaire, et ceux qui comprennent le code Gros-Grey... À la fin de cet article, vous devriez pouvoir rire de cette blague !
 La tour de Hanoï
La tour de Hanoï
Tour le monde connaît les tours de Hanoï, inventées par Édouard Lucas en 1883 : une tour de 7 disques empilés les uns sur les autres par ordre de tailles décroissantes le long d'un axe vertical. Le but du jeu est de transférer ces 7 disques sur un autre axe vertical, un troisième étant disponible, sans jamais poser de disque sur un disque plus petit ni prendre plus d'un disque à la fois.
A gauche, l'illustration originale de Lucas.
1 : Position initiale des 3 axes
2 : Position intermédiaire
3 : Position finale
Vous pouvez vous essayer au jeu avec cet applet.
Quel série de mouvement faut-il effectuer pour transférer entièrement la tour du premier au dernier axe ? Avec une démonstration par récurrence rapide, on peut montrer qu'il faut 127 déplacements pour atteindre ses fins.
En appelant 1, 2, 3, 4, 5, 6, 7 les anneaux du plus petit au plus grand, on s'aperçoit que l'ordre dans laquelle il faut déplacer les anneaux est :
1 2 1 3 1 2 1 4 1 2 1 3 1 2 1 5 1 2 1 3 1 2 1 4 1 2 1 3 1 2 1
6
1 2 1 3 1 2 1 4 1 2 1 3 1 2 1 5 1 2 1 3 1 2 1 4 1 2 1 3 1 2 1
7
1 2 1 3 1 2 1 4 1 2 1 3 1 2 1 5 1 2 1 3 1 2 1 4 1 2 1 3 1 2 1
6
1 2 1 3 1 2 1 4 1 2 1 3 1 2 1 5 1 2 1 3 1 2 1 4 1 2 1 3 1 2 1
Comme j'avais déjà fait un article sur les tours de Hanoï à cette époque (dont le début de cet article est un quasi copié-collé), je ne vais pas m'appesantir sur le sujet, et parler de tout autre chose (ou pas) ...
Le spin-out

Schéma du spin-out
Autre temps, autre jeu : c'est dans les années 70 que William Keister, informaticien à la retraite, profite enfin de ses beaux jours pour s'amuser sur des casse-têtes et inventer le spin-out. Ce jeu se présente sous la forme de deux lattes (bleue et grise sur l'illustration), la première étant munie de rebords et la seconde étant coincée entre ces rebords. Le but du jeu est de sortir la seconde latte de la première par la droite. Pour compliquer la chose, 7 éléments pivotants (se présentant à la verticale) sont fixés sur la latte que l'on ne peut sortir que lorsque tous ces éléments seront couchés. Le mécanisme est tel que l'on ne peut faire pivoter un élément que si celui à sa droite est levé, et une encoche dans le support ne permet de bouger que les éléments les plus à droite.
Je n'ai trouvé aucun applet permettant de spin-outer en ligne, il va falloir faire travailler son imagination...
 Un début de partie peut ressembler à ceci (en numérotant de 1 à 7 les éléments, en commençant par le plus à droite) :
Un début de partie peut ressembler à ceci (en numérotant de 1 à 7 les éléments, en commençant par le plus à droite) :
A - Initialement, tous les éléments sont levés, on peut faire pivoter seulement l'un des deux derniers.
B - Je choisis de faire pivoter celui qui est le plus à droite (1).
C - Puisque le dernier est couché, l'élément 3 est accessible.
D - On le fait pivoter.
E- Il nous faut à présent bouger l'élément 2, mais il est coincé par le 1. On revient alors au premier élément...
F - Que l'on fait pivoter.
G - Ce qui permet de passer au deuxième élément...
H - Pour le faire pivoter.
Pour la suite, il faudra revenir pour bouger l'élément 1. Les trois derniers éléments sont couchés : on aura accès au 4eme et au 5eme !
On peut résumer la résolution en disant qu'il faut alternativement bouger l'élément le plus à droite et l'élément le plus à gauche accessible.
Bref, un jeu vraiment prise de tête et qui en plus ressemble à celui des tours de Hanoï. Elle demande moins de coups (85 rotations seront nécessaire pour en venir à bout), mais si on regarde la suite des éléments qu'il faut faire bouger, on trouvera la suite suivante :
1 3 1 2 1 5 1 2 1 3 1 2 1 4 1 2 1 3 1 2 1
7
1 2 1 3 1 2 1 4 1 2 1 3 1 2 1 5 1 2 1 3 1 2 1 4 1 2 1 3 1 2 1
6
1 2 1 3 1 2 1 4 1 2 1 3 1 2 1 5 1 2 1 3 1 2 1 4 1 2 1 3 1 2 1
C'est la même suite que celle des mouvements demandés pour la tour de Hanoï, au détail près que le début est oublié. Le spin-out correspond en fait à une tour de Hanoï partiellement commencée.
Le baguenaudier

Un baguenaudier...
Autre temps, autre casse-tête : le jeu du baguenaudier (alias Puzzle Meleda) (alias anneaux chinois) a été inventé, selon la légende, par le soldat Hung Ming (181-234), pour occuper sa femme pendant qu'il tuait les méchants à la guerre. C'est le mathématicien Luca Pacioli (l'"inventeur" du nombre d'or) qui le décrit pour la première fois au début du XVIe siècle, mais il est mis en lumière en 1550 par J. Cardan, qui proposait l'idée de changer toutes les serrures du monde par des baguenaudiers (Idée stupide quand on sait le temps qu'il faut pour en ouvrir un...). C'est Lucas qui donnera pour la première fois une solution mathématique utilisant le code Gros.
Le baguenaudier se présente sous la forme de deux... euh... trucs coincés par une demie-douzaine d'anneaux.... Tant que je n'en aurait pas dans les mains, je crois que je ne pourrais pas en donner de meilleure description... Un casse-tête qu'on rangerait volontiers dans la catégorie "trucs emmêlés qu'il faut démêler", mais qui a plutôt sa place dans "copie avant l'heure des tours de Hanoï". Sa méthode de résolution demande de "déplacer alternativement l'anneau le plus à droite et l'anneau atteignable le plus à gauche"...
Pour dire plus simplement, le spin-out est un spin-off du baguenaudier, inventé pour en rendre les règles un peu plus accessibles (pas besoin de l'avoir en mains pour piger comment ça marche)
Le code Gros-Grey
Revenons-en donc au spin-out, et codons les différentes positions possibles, en notant 1 les éléments levés et 0 les éléments couchés. On part donc de la position 1111111, et il faut arriver à la position 0000000. La suite des positions est alors :
1111111
1111110
1111010
1111011
1111001
1111000
1101000
...
0000011
0000001
0000000
Cette façon de compter est celle du Gros-Grey : une façon binaire de compter où passer d'un entier au suivant ne demande que de changer un seul chiffre. Résoudre le problème du spin-out (ou du baguenaudier, ou des tours de Hanoï), c'est juste compter à l'envers et en Gros-Grey de 1111111 à 000000 !
Comme son nom l'indique, le code Gros-Grey a été inventé en 1872 par Louis Gros, clerc de notaire à Lyon. En 1930, Frank Grey (ingénieur des laboratoires Bell en théorie de la communication, et collègue de William Keister, tout concorde) réinvente le code.
| décimal | binaire | Gros-Grey |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 11 |
| 3 | 11 | 10 |
| 4 | 100 | 110 |
| 5 | 101 | 111 |
| 6 | 110 | 101 |
| 7 | 111 | 100 |
| 8 | 1000 | 1100 |
Il y a tout un tas de manières (équivalentes) de définir le Gros-Grey :
- Pour passer d'un nombre à un autre, on compte le nombre de '1'. S'il y en a un nombre pair, on change le dernier chiffre, et s'il y en a un nombre impair, on change le chiffre à gauche du '1' le plus à droite, qui peut éventuellement être un 0 muet ("Changer" signifier changer un 1 en 0 ou inversement)
- On peut les définir récursivement : si on connaît l'écriture des 2n premiers entiers (en partant de 0), on obtient les 2n suivants en les reprenant en ordre inverse et en ajoutant un '1' devant. Cette définition leur donne une jolie structure fractale !
- Pour passer d'un terme à un autre, il suffit de changer un seul chiffre. La position du chiffre à changer est donnée par la suite 1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2, 1, 5 qui est la "suite de la copie augmentée". Pour l'obtenir, on part de la suite "1", que l'on prolonge en la recopiant en ajoutant 1 à son dernier élément : on trouve successivement "1", "1,2", "1,2,1,3", "1,2,1,3,1,2,1,4"... C'est la suite des mouvements à faire pour gagner aux tours de Hanoï...
- On peut aussi définir ces nombres par les motifs suivis par les chiffres. Le dernier chiffre suit le motif "011001100110011...", l'avant dernier chiffre suit le motif "001111000011110000...". De manière plus générale, le k-ième chiffre suit le motif "0...0[1...10...0]", qui commence par 2k-1 '0', puis alternativement 2k '1' et 2k '0'.
- On peut enfin les définir à partir de leur écriture binaire. Pour coder l'entier n en Grey, on part de son écriture binaire : le k-ième chiffre (à partir de la droite) de n en Grey est donné par l'addition binaire sans retenue (ie, 1+1=0) du kième et du (k+1)ième chiffre de n en binaire. Par exemple, le nombre 24, qui s'écrit 110 000 en binaire donnera 101 000 (le 1 chiffre est 0 puisque 0+0=0, le 4eme chiffre est 1 puisque 1+0=1...).
La procédure inverse permet de transformer un entier de son écriture Grey en son écriture binaire. On trouve par exemple que le nombre qui en Grey s'écrit 1111111 s'écrira en binaire 1010101, autrement dit, 85 en décimal. C'est donc le nombre de mouvement nécessaire pour terminer le jeu du spin-out !
Comme je ne résiste jamais à recycler mes vieux scripts, je vous propose d'appuyer sur l'un de ces deux boutons, qui vont à votre place compter en Gros-Grey !
Le voyageur de commerce
Le codage Gros-grey ne sert pas qu'à résoudre des casse-têtes en bois artisanaux, mais permet de résoudre certains problèmes en électronique (c'est pas pour rien que Grey l'a inventé !). Il donne notamment une solution au problème du voyageur de commerce (dans le cas d'un hypercube).
Un voyageur de commerce doit visiter n villes réparties au quatre coins de la France. Le problème du voyageur de commerce est de trouver le chemin qui passe par toute les villes et qui minimise le chemin à parcourir. Le code Gray donne la marche à suivre dans le cas où les villes sont dans les 2n sommets d'un hypercube (un carré ou un cube, généralisé aux dimensions supérieures)
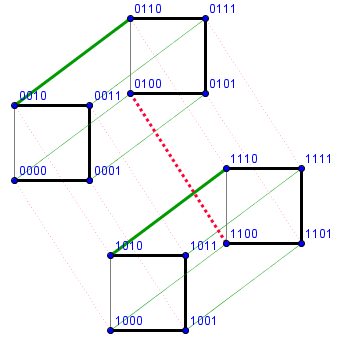
Un hypercube de dimension 4, chaque segment en représente une arrête.
En noir la première et deuxième dimension, en vert la troisième et en rouge la quatrième
Le chemin en gras est (l'un des) plus court chemin relient tous les sommets
En codant chaque sommet de l'hypercube par ses coordonnées, on obtient tout simplement l'itinéraire à suivre en Gros Grey ! On pourrait même généraliser le problème aux hyperpavés sans trop de difficultés...
Il est maintenant temps de relire la bonne blague du début :
Il existe 10 types de mathématiciens : ceux qui comprennent le binaire, ceux qui ne le comprennent pas et ceux qui comprennent le Gros Grey !
* Rires ! *
Sources :
- D'autres informations sur le Gros-Grey chez JB Roux
- Ou dans les cahiers de Ludo
- Ou chez Gérard Villemin
- Ou dans l’article Voyageurs et baguenaudiers de Jean-Paul Delahaye, Pour la science, No 238, août 1997



/http%3A%2F%2Fstorage.canalblog.com%2F78%2F22%2F210892%2F100064815_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F59%2F97%2F210892%2F93981751_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F47%2F50%2F210892%2F93681458_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F09%2F42%2F210892%2F76864656_o.png)