Problèmes de voisinages sur l'ile de Wada

Sur l’ile de Wada, perdue au milieu de l'Atlantique, trois royaumes indépendants se partagent les terres. Le Royaume du Naah’Oj, peuplé de guerrières et de guerriers forts et courageaux, mais bizarement pacifiques ; le Royaume de l’Ayhliuj, une nation de sages adeptes de la philosophie et des mathématiques, et le Royaume n°3, dont la principale caractéristique est de n'avoir aucune particularité. La paix y règne depuis des siècles.

L'ile est connexe par arcs, et chacun de ces royaumes est connexe par arcs (ie, on peut toujours aller à cheval d’un point A à un point B du royaume donné sans avoir à traverser la moindre frontière). De plus, chaque parcelle de terre de l’ile est occupée par l’un des 3 royaumes (sauf les points frontières, qui n'appartiennt à aucun royaume, mais leur taille est de mesure nulle).
Sur cette ile, combien existe-t-il au maximum de points triples, c’est à dire de points où trois royaumes se rejoignent ?

Avec deux trois coups de crayons, on peut facilement fabriquer un exemple où il n'y en a qu'un seul..

L'ile de Wada : trois royaumes, un seul point triple

Avec quelques coups de crayons supplémentaires, on peut se convaincre qu’il peut y en avoir deux, si l’un des royaumes est enclavé au milieu des autres.

L'ile de Wada II : trois royaumes, deux points triples.
Peut-on faire mieux ?

Mais est-ce possible d’en avoir au moins 3 ? Ou davantage ?

Eh bien, oui, il est même possible qu’il y ait une infinité. Pire, il est possible que chacun des points de la frontière soient des points triples ! Une telle carte a été imaginée en 1917 par le mathématicien japonais Kunizo Yoneyama, reprenant selon lui l’idée de Takeo Wada, lui aussi japonais et mathématicien.
À vrai dire, je voulais parler de ce problème dans mon article/vidéo sur le théorème de Jordan, parmi les nombreux objets étranges liés à la démonstration du théorème. Je n’ai pas retenu l’idée, pour éviter le hors-sujet, mais il me semble important de tout de même en parler. Les courbes continues partout et dérivables nulle part et les courbes remplissantes permettent de saisir la complexité de la notion de courbe ; la sphère cornue d’Alexander permet de comprendre que la notion d’extérieur ou d’intérieur n’est pas complètement triviale. Les royaumes de Wada, quant à eux, obligent à regarder de plus près la notion de frontière.

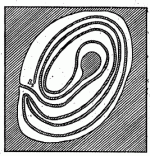
Le lac de Wada tel qu'il apparait pour la première fois en 1917 dans l'article de Yoneyama

En fait, c’est quoi une frontière entre deux domaines ? Sans rentrer dans les détails techniques, on dit qu’un point est à la frontière de deux ensembles distincts A et B si, quand on trace un disque (arbitrairement petit) autour de ce point, il y aura toujours au moins un point du disque qui appartient à A, et un autre qui appartient à B. Une frontière se doit donc d’être d’épaisseur nulle, sans quoi on pourrait y glisser un tout petit disque.
De même, on peut définir un point triple entre trois ensembles distincts A, B et C comme étant un point tel que tout disque (arbitrairement petit) autour de ce point contiendra au moins un point de A, de B et de C.

Le point A n'est pas un point frontière : on peut trouver un disque autour de A inclut dans un seul domaine
Le point B est un point frontière : tout disque, même tout petit, autour de B chevauche au moins deux domaines
Le point C est un point triple : tout disque, même tout petit, autour de C chevauche trois domaines

Welcome to Wada Island
Revenons sur notre ile, et regardons jours après jours comment celle-ci a été colonisée. Il se trouve que cette ile est un carré de 270km de côtés, cela va nous arranger pour les calculs.

Année 0. L'ile est sauvage.
Chaque carreau a pour côté 10km.

Année 1 : Les colons de Naah’Oj arrivent par le milieu de la côte ouest, et colonisent l’ile au maximum de façon à laisser 90 km de zones libres entre le royaume et les côtes Nord, Est et Sud (une tradition de ce peuple est de toujours laisser des zones libres pour que d'autres peuples puisse également s'y installer). Ils occupent donc 2/9 des terres disponibles.

Année 1 : tout point de la bande blanche est à moins de 90km du royaume.

Année 1 + ½ : Les colons de l’Ayhliuj débarquent en zone libre, au milieu de la partie nord de la côte ouest. Ils ne sont pas venus en guerre, ils décident donc de s’étendre sur la zone vierge, en faisant en sorte de toujours laisser 30 km de no man’s land entre le royaume et le reste du monde (mer ou royaume de Naah’Oj).

Année 1.5 : tout point de la bande blanche est à moins de 30km d'un royaume.

Année 1 + ½ + ¼  : les colons du Royaume n°3 débarquent à présent, dans la partie libre la plus au nord de la côte ouest. Le royaume va lui aussi s’étendre, en restant dans la bande de 30km laissée par le royaume de l’Ayhliuj. Pour ne pas s’attirer de problèmes, ils gardent dans leur conquête une marge de 10 km entre eux et les autres royaumes ou côtes
À ce stade des camganes de colonisation, il n’existe pour l’instant aucune frontière entre ces trois régions, seulement une bande large de 10 km.

Année 1.75 : tout point de la bande blanche est à moins de 10km d'un royaume.

Année 1 + ½ + ¼ + ⅛ : Voyant les autres royaumes s’installer, Naah’Oj entreprend une nouvelle campagne d’extention. Dans la bande 10 km encore vide, ils s’étendent de façon à laisser une bande large de 3.333...km entre toutes les autres frontières

Année 1.875 : tout point de la bande blanche est à moins de 3.33km d'un royaume.

Jours suivants : Les uns après les autres, les différents royaumes vont s’étendre chacun leur tout dans les bandes laissées libres à l’étape précédente, de façon à ce que ces bandes soient à chaque étape d’une largeur trois fois plus petites.

Année 2 : tout point de la bande blanche est à moins de 0km d'un royaume.

À la fin de la deuxième année, chaque royaume aura réalisé une infinité de campagnes d’extension. La bande séparant les différents royaumes ne peut plus être qualifiée comme telle ; bien qu’elle existe encore, sa largeur est d’épaisseur nulle, cette bande est donc la frontière entre les trois royaumes. Mais surtout, la construction que l’on vient de faire permet d’affirmer que chacun des points est un point triple.


Pour voir cela, prenons un point quelconque de cette frontière, et traçons autour un petit disque. Étant donné qu’à chaque étape de la construction, la bande a été divisée par trois, il y a forcément une étape de la construction durant laquelle la bande passait au travers de ce disque. Durant les trois étapes suivantes, de parties de la bande se sont faite annexer par chacun des trois royaumes : il y a bien un point de chaque ensemble dans ce petit disque, c’est un point triple ! C’est donc l’ensemble des points de la frontière qui sont des points triples !

Détail d'un point autour d'une bande rouge.
N'importe quel disque tracé autour d'un point de la frontière chevauchera chacun des trois ensembles.

En fait, ce qui défie l’intuition dans cette construction, c’est que les points triples en questions sont bien des points triples au vu de la définition que l’on a donné plus haut, mais ce ne sont pas des points triples en forme de Y auquel on pouvait s’attendre.

Les fractales de Newton
On retrouve le principe des royaumes de Wada dans beaucoup de fractales. Un exemple pas trop compliqué est celui des fractales de Newton. Le principe est le suivant : on choisit un nombre complexe z₀ ∈ ℂ, et on calcule la suite définie par z_n+1 ⟼ z_n - p(z_n)/p’(z_n), avec p une fonction polynomiale. En général, cette suite convergera vers l’une des racines de ce polynôme, c’est le principe de la méthode de Newton pour calculer numériquement les racines d’un polynôme.
Prenons par exemple la fonction p(z) = z³–1, qui possède trois racines : 1, – 0.5 + √3/2 i et – 0.5 – √3/2 i. En choisissant le nombre z₀ = 10, la suite z_n+1 = z_n - (z_n³–1)/(3 z_n²) donnera z₁ = 6.67, z₂ = 4.54, z₃ = 2.98, etc. Cette suite converge vers 1, qui est bien une racine du polynôme.
En partant de z₀ = i, la suite convergera vers -0.5 + √3/2 i.
On peut alors s’amuser à colorier les points z₀ en fonction de point vers laquelle la suite converge, ce qui donne ce que l’on appelle les fractales de Newton.

Fractale de Newton associée au polynôme p(z) = z³–1.
Les différentes couleurs correspondent aux trois bassins d'attraction des racines de p.

Non seulement, ces fractales sont très jolies, mais on y retrouve la propriété des royaumes de Wada : on a construit trois ensembles, et tout point de la frontière est un point triple.

On peut bien sûr étendre le concept, et fabriquer des ensembles où tous les points de la frontière sont des points quadruples, comme cette fractale obtenue par la méthode de newton sur le polynôme p(z) = z⁴-1.

Fractale de Newton associée au polynôme p(z) = z⁴ – 1.

Je vous laisse imaginer comment obtenir une fractale de Newton où tous les points frontières sont duoquadruple...

---

Sources :
Lakes of Wada - Wikipedia
Theory of continuous Set of Points, Kunizô Yoneyama

Comments

[Thomas]

Un autre point des plus perturbants dans tous ces objets curieux, que j'illustrerais avec les fonctions continues partout dérivables nulle part, c'est que l'objet final que l'on présentera ne sera qu'une limite de suite de fonction qui conservera la continuité grâce aux théorèmes de convergence uniformes, bien que de l'intuition de la continuité , n'en restera pas grand chose. Impossible de tracer cette fonction pour le commun des mortels ! Pour ça, il faudrait l'atteindre, cette année 2. Tu m'expliques comment faire Eljj ?

Perso j'ai essayé de la manière suivante : j'ai sauté l'année 1,5, l'année 1,75 et même l'année 1,99999999999872678625. Et ça m'a pas pris bien longtemps ! pour ma fonction continue partout nulle par dérivable, j'ai juste fait un truc vaguement affine par morceau tout bidon sur un beau tableau de 3 mètre de large et j'ai juste mis pour le premier point anguleux de ma courbe x=1/(3→3→3→3→3→3→3→3→3→3→3→3→3→3→3→3→3→3→3). J'ai fait les choses en plutôt grand, non ? Et à côté de mon tableau qui doit se prolonger jusqu'aux confins de l'univers et au delà, j'ai juste mis 3 ptits points, tout tranquille.

L'an 2 il est à portée de main quoi. On est le 31 décembre de l'an 1, 23h59, 59 secondes et des 99999 à en remplir les feuilles A4 de la terre entière. Mais quand je tends le bras pour l'atteindre, j'ai un soucis ! Un blocage je dirais. Avant de l'atteindre, je dois faire la moitié de la distance qui me sépare à lui. Et je recasse encore mes segments ! Et une fois cette distance l'opération effectuée, le problème reste identique ! On m'avait pourtant dit que le paradoxe de la flèche qui n'atteint pas sa cible n'en était pas un !