Don't panic !

Nous sommes aujourd'hui le 10 octobre 2010, et le monde geek est en effervescence : Twitter ne parle que de ça, le hashtag #Binary fait le top buzz facebook skype twitt du jour...

10 octobre 2010, ça donne 10/10/10, voire même 101010. Aujourd'hui est un jour binaire, mais c'est bien plus que ça : 101010, en binaire, ce n'est autre que le nombre... 42 !

42 !

Quarante-deux ! C'est LA réponse à la grande question, sur la vie, l'univers et le reste, la réponse qui donne le sens de la vie ! C'en est même une constante fondamentale de l'Univers, au même titre que la vitesse de la lumière dans le vide ou la constante de Planck !

Non, l'auteur de ce blog n'a toujours pas pris de substances hallucinogènes. L'origine de tout ça, c'est H2G2, le guide du voyageur galactique, un monument de la culture geek créé à la fin des années 70 réunissant une trilogie de 5 livres, un feuilleton radio et tout un tas de choses qui en dérivent. L'histoire relate essentiellement les pérégrinations à travers l'Univers de l'anglais moyen Arthur Dent, suite à la destruction de la Terre, remplacée par une voie express hyperspatiale. On y apprend que la réponse à la grande question sur la vie, l'Univers et le reste, calculée par super-ordinateur Pensées Profondes en 7,5 millions d'années de calculs, est 42. Malheureusement, l'ordinateur en question n'était pas assez puissant pour en calculer la question correspondant à cette réponse...

De nombreuses questions sont envisagées :
- Combien de routes un homme doit parcourir ?
- Qu'est-ce qui est jaune et dangereux ?
- Pensez à un nombre, n'importe lequel.
- Combien font 9 fois 7 ?

Mais j'ai d'autres questions en tête, comme...

Donnez-moi un nombre de Harshad en base 10...
Parce que 42 est divisible par 4+2 : un nombre est dit "de Harshad" s'il est divisible par la somme de ses chiffres.

Quel est le deuxième plus petit nombre sphénique ?
Parce 42=2×3×7 : un nombre est sphénique s'il est le produit de exactement trois nombres premiers différents.

Donnez-moi un nombre oblong...
Parce que 42=6×7 : un nombre est oblong (ou pronique (ou hétéromécique)) si c'est le produit de deux entiers consécutifs.

Donnez-moi un nombre pratique...
Parce que les diviseurs propres de 42 sont 1, 2, 3, 6, 7, 14, 21, et que 4=1+3, 5=3+2, 8=7+1, 9=6+3, ... , 41=21+14+3+2+1: un nombre est pratique si on peut écrire tous les entiers inférieurs comme somme de ses diviseurs

Donnez-moi un auto-nombre...
Parce que 42 ne peut pas s'écrire sous la forme (10a+b)+a+b : un nombre n'est pas un auto-nombre si on peut l'écrire comme la somme d'un nombre et de ses chiffres (par exemple, 48 n'est pas un auto-nombre, puisque 48=42+4+2).

Quel est le cinquième nombre de Catalan ?
Parce que 42 = C_2×5⁵-C_2×5^5-1.
De manière équivalente, il y a 42 façons de mettre des parenthèses dans l'expression abcdef : par exemple, a((bc)(de))f, a(b(c(d(ef)))), ((ab)(cd))(ef)...
De manière équivalente, il y a 42 façons de trianguler un heptagone :

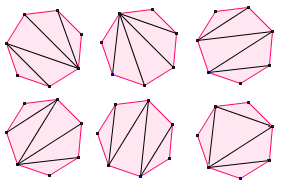
6 triangulations, parmi les 42 existantes

De manière équivalente, il y a 42 façons de parcourir une demi-grille 5x5 :

6 chemins, parmi les 42 existants

Quel est le troisième nombre pentadécagonal ?
Avec 42 billes, on peut former 2 pentadécagones (polygone à 15 côté) imbriqués, de la même façon que 25 est le 5ème nombre carré, puisque l'on peut former 4 carrés imbriqués :

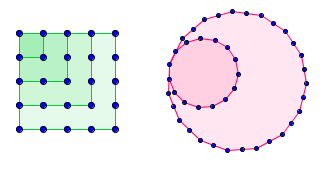
A gauche, 4 carrés imbriqués figurant le 5eme nombre carré (25)
A droite, 2 pentadécagones imbriqués, figurant le 3eme nombre pentadécagonal (42)

Quel est le 4ème nombre méandrique ?
Parce qu'il y a 42 façons de faire 8 intersections entre une courbe fermée et une droite. Le n-ième nombre méandrique est le nombre de façons dont peuvent se couper en 2n intersections une droite et une courbe fermée. Ce problème, à mi-chemin entre topologie et combinatoire, n'a toujours pas de solutions...

6 exemples de courbes fermées isotopiquement différentes ayant 8 points d'intersection avec une droite, parmi les 42 possibles

Donnez-moi un exemple de nombre de Størmer...
Parce que 42²+1=1765, et que son plus grand facteur premier, 353, est plus grand que 2x42=84 : un nombre est de Størmer si le plus grand facteur premier de n²+1 est supérieur ou égal à 2n.

Donnez-moi un exemple de nombre brésilien...
Parce que 42 s'écrit 222 en base 4 : un nombre est brésilien si l'on peut trouver une base dans lequel il peut s'écrire avec un seul chiffre répété.

Quel est le 6ème nombre de Bernoulli ?
Parce que 1/42 apparaît naturellement dans le développement en série entière de x/(e^x-1) (Les nombres de Bernoulli ont leur importance en analyse, et apparaissent notamment dans la fonction ζ de Riemann) :

Dites-moi un truc marrant sur les décimales de pi...
Parce que les décimales de pi, à partir de la 242422e décimale, sont 42424242...

Et je crois que j'oublie d'autres détails absolument importants, comme le fait que 666×667=444222 ; que 42 est la somme de deux nombres premiers consécutifs (42=19+23) ; que la plus petite façon d'écrire 1 en une somme de 4 fractions différentes est 1=1/2 + 1/3 + 1/7  + 1/42 ;  que le nombre 10 peut s'écrire comme somme d'entiers non nuls de 42 façons différentes ; qu'un nombre de la forme n⁷-n est toujours divisible par 42 ; que Gutenberg a imprimé la Bible avec 42 lignes par pages ; que le nombre préféré de docteur House est 42 ; que...

Bref, en ce 10 octobre 2010, je vous souhaite un happy 42 day !
Et n'oubliez surtout pas votre serviette !

---

Jeu bonus :
Depuis l'article du 30 août 2009, intitulé Savez-vous compter les choux ?, les 42 font régulièrement des interventions sur le blog. En fait, les 54 derniers articles de ce blog possède chacun un (voire plusieurs) "42", plus ou moins bien cachés ... Parviendrez-vous à tous les débusquer ?...

Comments

[Seb]

Incroyable...

Et 1010101010 en base 10101010 (=170) s'écrit 42

Et 101010101010 en base 1010101010 (=682) s'écrit 42



Et cela se généralise facilement:

En base 2: 101010...10 (répété n fois) s'écrit en base 10:

Un = Sum(2^(2n-1)) = 2/3(4^n-1)

On a Un+1 = 4*Un + 2



Et donc Un+1 s'écrira toujours 42 en base Un

[JeanTwix]

Tiens, je repense à un truc amusant qu'un ami m'a fait remarquer à ce propos :
101010 est l'expression en binaire de 42 ;
En "rajoutant un 10", on obtient :
10101010, soit 170, qui exprimé en base 42, donne... 42.
C'est fou.

[El Jj]

Pas bête, Fireblade ! Dommage que je ne puisse choisir les secondes !

[Fireblade]

Quitte à modifier l'heure du post, autant mettre 10h10m10s... non? :D

[Professeur Miche]

Vous avez vraiment réussi à poster à 17h42 ou vous avez modifié l'heure?