Deuxième dimanche après Noël

Jeudi dernier, c'était le 6 janvier. Et environ 2010 ans plus tôt, Melchior, Balthazar et Gaspard ont apporté au petit Jésus quelques babioles achetées vite fait chez Nature & Découverte. Depuis ce jour, pour fêter cet évènement, la tradition veut que l'on glisse une fève dans une galette à la frangipane pour décider de celui qui deviendra roi à la place du roi. Officiellement, l'épiphanie a lieu le 6 janvier, mais, bien que les magasins la fêtent entre fin novembre et début février, la tradition demande qu'elle soit fêtée le deuxième dimanche après Noël. Dimanche dernier c'était pas pratique, donc c'est aujourd'hui que l'on se réunit en famille, le petit dernier sous la table, pour déguster la galette des rois !

Seulement, sans doute à cause de l'intervention de forces obscures ou de Murphy, le membre de la famille assigné à couper la galette sera une fois de plus la risée de l'assemblée. "Mais, enfin Jacqueline, comment tu fais pour toujours couper sur la fève ?".

Sans son esprit d'escalier, Jacqueline aurait pu s'en sortir. Plutôt que de partir en pleurs, elle aurait dû rétorquer quelque chose comme : "Oui, bon ben, eh ! J'avais à peu près une chance sur 4 de tomber dessus, c'est pas de ma faute s'il n'y a que toi ici qui peux prétendre avoir une chance de cocu !". Car, oui Jacqueline, les probas sont tes amies !

Résolution du problème
La question est donc : quelle est la probabilité de tomber sur la fève en coupant la galette ?

Déjà, quelles sont les données ?

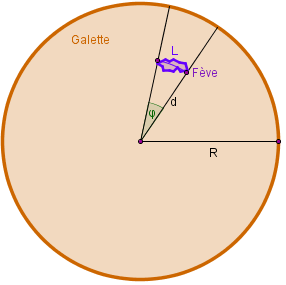
• R, le rayon de la galette
• L, la taille de la fève. La seule chose intéressante ici, c'est seulement le diamètre de la fève qui apparait depuis le centre de la galette. Étant donné la taille de la fève, on supposera que ce diamètre est égal à la longueur de l'arc correspondant.
• d, la distance entre la fève et le centre de la galette. Si votre pâtissier n'est pas trop stupide et n'a pas mis la fève au centre de la galette, on a 0 ≤ d ≤ R.
• φ, le diamètre apparent (qui est un angle) de la fève depuis le centre de la galette. Cet angle peut être approché par la formule φ≃L/d (si l'angle est exprimé en radians).
• n, le nombre de personnes qui veulent se partager la galette.
• Et on cherche respectivement les probabilités p(L,d,n) (abrégée p_n) et q(L,d,n) (abrégée q_n) de couper la fève et de ne pas couper la fève (évidemment, q_n=1-p_n)

J'aime la galette, savez-vous comment ?...

Il est maintenant l'heure de couper la galette. Commençons par un premier coup de couteau. Puisqu'ici, on modélise le problème, on ne coupera pas selon le diamètre de la galette, mais selon un rayon.

On choisit donc un rayon de la galette. La probabilité de tomber sur la fève est celle de choisir un rayon dans le secteur de la fève, soit p₁ = φ/2π. La probabilité de ne pas couper la fève est donc q₁ = 1 - φ/2π.

Sauf qu'il n'y a pas un seul invité, mais n. Il faudra donc couper la galette n fois, sans jamais tomber sur la fève. La probabilité est donc de...

Pour dire ce genre de chose, il faut quand même supposer que chaque coup de couteau est indépendant du précédent, ce qui revient à dire que l'on donne sans réfléchir n coups de couteaux, sans forcément essayer de faire des parts égales les unes aux autres.

En fait, non, les coups de couteaux ne sont pas du tout indépendants ! Une fois le premier coup de couteau donné, on donnera le deuxième après l'avoir décalé d'un angle de 2pi/n, l'angle d'une part. Finalement, seul le premier coup de couteau est intéressant dans l'histoire, on déduit les autres par rotation. On peut donc se contenter de regarder comment on donne le premier coup de couteau dans un secteur correspondant à la taille d'une part. On peut même supposer que la fève est dans cette part là.

Quand elle est bien faite, avec de la frangipane dedans !

On peut donc supposer que le premier coup de couteau tombe dans le secteur de référence. Les autres coups de couteaux éviteront à coup sûr la fève, tandis que le premier l'évitera avec une probabilité de...

(Et donc, p_n = nL/2dπ)

En fait, si la fève est suffisamment petite et qu'il n'y a pas trop de monde, les deux formules donnent des résultats similaires.

Application numérique
Et dans la pratique, qu'est ce que ça donne ?

Prenons une galette standard de supermarché de 30 cm de diamètre (R=15), et on met la fève aux 2/3 du rayon (d=10). La dimension de la fève est standard (L=2) et 8 invités sont présents (n=8). On met le tout dans la machine, et on trouve...

p₈ = 0.25...

Bref, 25% de (mal)chance de couper sur la fève !

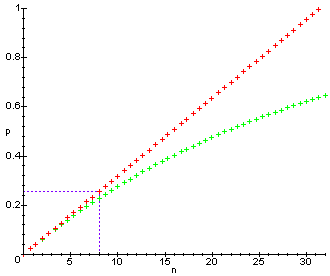
Probabilité p de couper sur la fève en fonction du nombre n de convives (en rouge en supposant les coups de couteaux dépendants, en vert en les supposant indépendants)

Si on teste sur la galette 6 personnes de la boulangerie du coin (R=10, d=6, L=2, n=6), la calculatrice donne p₆ = 0.32... Argh, une chance sur 3 de couper sur la fève !

Après, les choses se compliquent terriblement si, comme belle-maman, on place deux fèves dans une galette des rois pour 8 personnes pour contenter tout le monde... La probabilité d'avoir la fève augmente, mais moins vite que celle de couper sur la fève...

---

Sources :
L'article que vous venez de lire est très fortement inspiré de l'omnilogisme De la probabilité de tomber sur la fève en coupant la galette des rois de Neamar.

Comments

[Terry Laire]

Mais où trouvez-tu des idées pareilles... Quel terrain miné, même pour une fève assez loin du centre ! D'ailleurs, quelle est la distribution de probabilité de d ? :P