Allez venez ! Milnor

John Milnor, 80 ans. Si vous êtes loin du monde des maths, vous n'avez probablement jamais entendu parler de lui. Si vous êtes dans le métier, vous avez peut-être déjà entendu ce nom, au détour d'une conversation des collègues à la cafèt. Par contre, si vous êtes géomètre (au sens large), vous avez forcément l'un de ses bouquins dans votre bibliothèque préférée... Pour la première moitié de ses travaux en topologie, on lui a décerné en 1962 la médaille Fields ("le prix Nobel des mathématiques"). Mais c'est le 23 mars dernier que Milnor fait à nouveau parler de lui, en recevant le vrai prix Nobel des maths : le prix Abel !

John

C'est donc mercredi dernier que l'académie Norvégienne des Sciences et des lettres a décerné à l'américain John Willard Milnor le prix Abel « … pour ses découvertes novatrices en topologie, géométrie et algèbre». Un prix amplement mérité, puisque Milnor peut être considéré comme le fondateur de la topologie différentielle, l'un des domaines les plus étudiés aujourd'hui.

Une sphère exotique en dimension 7

Sphère exotique, vu à la télé

La réalisation la plus célèbre de Milnor, obtenue un peu par hasard, restera la découverte d'une sphère exotique : homéomorphe à une sphère mais pas difféomorphe. Grâce à elle, il a fait comprendre au monde que quand on mélange la topologie et le calcul différentiel, on trouve quelque chose de nouveau (la topologie différentielle), et pas juste de la topologie où les calculs ont été simplifiés. Homéomorphe ? Difféomorphe ? Quelques explications sont demandées.

On parle ici de topologie : on s'intéresse à ce qu'il se passe quand on déforme sans déchirer des objets mathématiques. Plus particulièrement, que se passe-t-il quand on déforme des sphères ?

Prenons par exemple une sphère de dimension 2 (aussi appelée "cercle"). On le prend, on l'étire, on le tord, on fait des plis, on défait les plis, mais sans le déchirer ni faire fusionner deux points. On obtient alors une courbe fermée. Puisqu'on peut déduire l'un des deux objets à partir de l'autre par une simple déformation, on dit qu'ils sont homéomorphes. Si, en plus, la déformation qui transforme les deux objets est lisse (Au cours de la déformation, on n'a pas formé de plis anguleux ou des trucs comme ça), on dit que les deux objets sont difféomorphes.

Un cercle (sphère de dimension 1) et une courbe de Jordan. Ces deux objets sont homéomorphes (et difféomorphes)

On peut facilement trouver des déformations qui sont des homéomorphismes, mais qui ne sont pas des difféomorphismes (il suffit de faire des plis). Cependant, étant donné deux objets bien lisses, il n'est pas forcément évident de dire que si on peut trouver une déformation transformant l'un en l'autre (un homéomorphisme),  on peut trouver une version lissée de cette déformation (un difféomorphisme)...

Les objets qui intéressent particulièrement les topologues, ce sont les variétés, des objets bien lisses qui, en tout point, ressemblent un peu à un espace euclidien de dimension n (à une droite, à un plan, à un espace tridimensionnel...). Notons au passage que la dimension d'un objet topologique est la dimension de l'espace à qui il ressemble, pas la dimension de l'espace qui l'entoure (un cercle, qu'il soit dans un plan ou dans l'espace, restera de dimension 1).
Les variétés les plus fondamentales, ce sont les sphères. On en a de toutes dimensions : de dimension 0 (deux points), de dimension 1 (un cercle), de dimension 2 (une sphère "ballon"), ou de dimensions plus grandes (même si elles sont plus difficiles à imaginer). La question qui se pose alors, c'est de savoir si un objet qui est homéomorphe à une sphère lui est toujours difféomorphe. Le problème, c'est que dans les petites dimensions, les plus faciles à se représenter, la question est relativement facile, mais non généralisable.

En 1956, John Milnor, alors en train d'étudier les variétés de dimension 7, tombe sur un objet étrange. Ce n'est pas une sphère à proprement parlé, mais elle lui est très similaire. Il pense d'abord à un contre-exemple de la conjecture de Poincaré (un objet partageant les bonnes propriétés avec la sphère est homéomorphe à une sphère - qui sera démontré pour cette dimension six ans plus tard). Après avoir regardé de plus près, il s'aperçoit que l'objet en question est bien homéomorphe à la sphère mais, coup de théâtre, ne lui est pas difféomorphe ! On parle alors de cette sphère comme étant "une sphère exotique". Quand on essaye de passer de la sphère exotique à la sphère classique par déformation, on est obligé de créer des plis impossibles à annuler (de la même façon qu'un pli se forme quand on ne repasse pas très bien son jean).

Comment créer soi-même sa sphère exotique ? Puisque nous ne vivons pas dans un monde à 8 dimensions, ça va être compliqué de le fabriquer réellement... Par contre, c'est un peu plus facile d'un point de vue conceptuel : des exemples de sphères exotiques peuvent être obtenues en tordant une sphère.
Pour ça, regardons plutôt les petites dimensions : quand on remplit une sphère (de dim n), on obtient une boule (de dim n+1), dont le bord est la sphère. Cette sphère, on peut l'obtenir à partir de deux boules de dimension n que l'on recolle le long de leur bord (une sphère de dimension n).

Cette construction se voit bien en petites dimensions. En recollant deux boules de dimension 1 (des segments) le long de leur bord (le bord d'un segment, c'est deux points : une boule de dim 0), on trouve bien une sphère de dimension 1 : un disque.

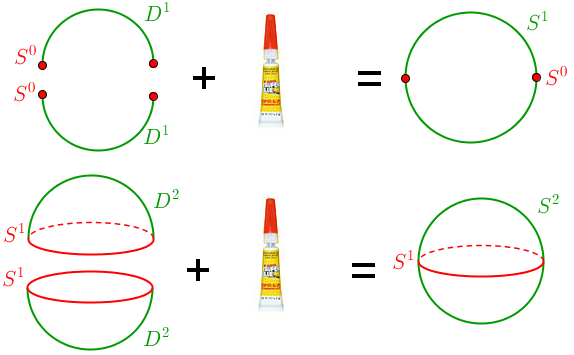
Pour obtenir un cercle, on peut recoller deux segments (disques de dim 1) selon leur bord (deux points).
Pour obtenir une sphère, on peut recoller deux disques (de dim 2) le long de leur bord (un cercle)

De la même façon, quand on recolle deux disques (une boule de dimension 2) le long du cercle qui leur sert de bord, on trouve notre bonne vieille sphère de dimension 2. On encore, pour obtenir une sphère de dimension 4, il suffit de recoller deux boules pleines le long de leur bord.
Finalement, en recollant deux boules de dimension 7 le long de leur bord (une sphère de dimension 6), on trouve une sphère de dimension 7. Mais ce recollement, il n'y a pas une seule façon de le faire. Quand on ne prend pas le bon, on tombe sur l'une de ces sphères exotiques.

Fort de sa découverte, Milnor s'est attelé à dénombrer les sphères exotiques dans toutes les dimensions. En dimension 7, il en recense alors 28 ! Alors qu'il n'y a qu'un seul type de sphère en dimension 5 ou 6, Milnor en découvre 2 en dimension 8, 8 en dimension 9, 6 en dimension 10, 992 en dimension 11 ou 523264 en dimension 19...

On découvrira plus tard (Donaldson, en 1983) un nouvel exemple d'espace exotique, cette fois-ci en dimension 4, appelé "R⁴ exotique".

Le Hauptvermutung
(J'ai toujours adoré les théorèmes ou les conjectures qui ont su garder leur nom allemand)

Mais Milnor n'est pas connu que pour sa sphère exotique, il a laissé ses traces dans d'autres domaines de la topologie, notamment dans l'histoire de la conjecture que l'on appelle "Hauptvermutung" (conjecture principale, en allemand), qui parle de triangulation d'espace topologique.

Prenons par exemple une variété à deux dimensions (une sphère, pour être original). Cet espace, on peut le trianguler : découper l'espace en petits triangles (en dim 2) / tétraèdres (en dim 3) / simplexe de dimension supérieure (en dim n).

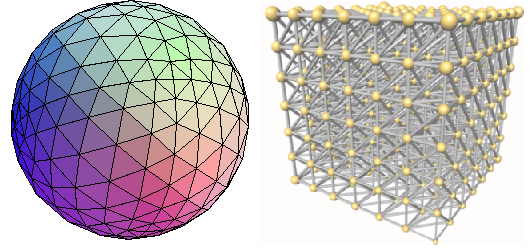
Triangulation d'une sphère (par des triangles) et d'un cube (par des tétraèdres)

Trianguler un espace, ça sert surtout à le découper en petites cellules plus faciles à étudier. Seulement voilà, même s'il semble à peu près évident que toute variété peut être triangulée, on ne sait pas bien (dans les années 50) le démontrer.

Sauf que, notre sphère, on peut la trianguler bien autrement. Déjà, on peut la raffiner, en triangulant les triangles intervenant dans cette triangulation ; on en obtient une nouvelle, qui partage sensiblement les mêmes propriétés que sa mère. On alors, on peut prendre une toute autre triangulation, qui n'a a priori aucun rapport avec la première.

Une autre triangulation de la sphère (oui, c'est un icosaèdre). A-t-elle un raffinement commun avec l'autre ?

La question soulevée par le Hauptvermutung (1908), c'est de savoir si deux triangulations d'un même espace peuvent être toutes les deux raffinées en une même sous-triangulation. Si c'est bien le cas, les deux triangulations partagent les mêmes propriétés, caractéristiques de l'espace en question.

En deux dimensions, le Hauptvermutung est vrai : il existe toujours au moins une triangulation, et deux triangulations ont toujours un raffinement commun, ce qui prête à penser que c'est encore le cas en dimensions plus grandes.

C'est là (1961) que Milnor intervient, en trouvant toute une famille de contre-exemples bien sentis dans toutes les dimensions supérieures à 6. Quelques années plus tard, d'autres contre-exemples seront découverts dans le cas moins général des variétés. Le coup de grâce sera donné en 1982, lorsque Freedman découvrira une variété de dimension 4 qui ne peut même pas être triangulée !

Le théorème de la boule chevelue
Peut-on coiffer une noix de coco sans faire d'épis ? C'est l'objet du théorème de la boule chevelue, pas du tout démontrée par Milnor (mais par Brouwer) en 1912, qui dit que c'est impossible.

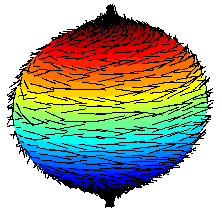
Quand on essaye de coiffer continument une sphère, on finit toujours par créer un épi quelque part

Impossible, peut-être, mais pas pour Milnor... il n'y a qu'à changer de dimension ! En fait, Milnor cherche plutôt une généralisation de la question : quelles sont les sphères qui sont parallélisables.

Reprenons la sphère de dimension 2 vue depuis l'espace de dimension 3 : en tout point, on peut dessiner un plan tangent. Ce que l'on aimerait faire, c'est munir chacun de ces plans d'un repère (x,y) (2 vecteurs perpendiculaires) de manière à ce que deux points proches disposent grosso-modo du même repère, ceci afin de munir la sphère entière d'un joli repère. Mais est-ce vraiment possible ? Et dans les autres dimensions (trouver un repère à n vecteurs en tout point de la n-sphère) ? On dira alors que la n-sphère est parallélisable.

D'après le théorème de Brouwer, c'est impossible sur la sphère de dimension 2 (on ne peut pas trouver un seul champs de vecteur potable, alors 2...). Par contre, les sphères de dimension 1, 3 et 7 sont parallélisables (et ce sont les seules) ! Pour sa démonstration, Milnor fait intervenir la généralisation des nombres complexes : les quaternions et les octonions.

La 1-sphère est parallélisable, en prenant des vecteurs perpendiculaires au rayon (c'est l'esprit de la démonstration en dimension 3 et 7)

Milnor profite de ses recherches sur le sujet pour offrir en 1978 une toute nouvelle démonstration du théorème de la boule chevelue qui sort des sentiers habituels.

Plein d'autres choses
Mais Milnor, c'est aussi un théorème sur la courbure des nœuds qu'il démontre à 19 ans. C'est aussi un théorème en théorie des groupes (sur la croissance des groupes)  qui sera amélioré par Gromov (Prix Abel en 2009). C'est aussi une conjecture en K-théorie algébrique qui vaudra à Voevodsky une médaille Fields en 2002. Et c'est aussi un livre de référence en dynamique complexe...

La dynamique complexe est la branche des mathématiques qui étudie ce genre de dessin

Bref, cette année, le prix Abel n'est pas décerné au plus mauvais des mathématiciens vivant...

---

Sources :
The work of John Milnor, par W.T. Gowers

Comments

[Mathwise Gamgee]

Je suis tombé par hasard sur votre blog. Il est vraiment très intéressant, au moins pour les "matheux". Continuez !
Je pense que je parlerai de votre blog à quelques-uns de mes élèves lycéens, au moins ceux qui veulent en savoir plus sur les maths.

[Gaurbhack]

La sphère exotique donne faim! (même si j'ai aucune idée de ce que c'est)