La randonnée du carré
Au hasard de pérégrinations dans la webosphère mathématique, on tombe parfois sur de jolis problèmes dont l'énoncé pourtant simple amène à des difficultés insoupçonnées. Un problème de ce genre est d'autant plus beau qu'il est parfaitement anecdotique, sans applications pour encore longtemps et toujours au rang de conjecture ! Le genre de théorème suffisamment riche pour avoir un article à son nom sur le blog. Un bon exemple : la conjecture de Toeplitz (aka le théorème de Stromquist ou problème du carré inscrit).
Tous les ingrédients sont là :
- un problème simple à mi-chemin entre géométrie et topologie (autrement dit, avec des dessins)
- une période de 78 ans entre le moment où Otto Toeplitz énonce sa conjecture (1911) et le moment où Walter Stromquist publie une solution intéressante (1989).
- de chouettes variantes
Le problème du carré inscrit
Puisque le problème parle de courbe, il va falloir se munir d'un crayon et d'une feuille de papier. Dessinez-y une courbe qui revient à son point de départ, mais qui ne passe jamais deux fois au même endroit (c'est ce qu'on appelle une courbe de Jordan, qui partage le plan en un intérieur et un extérieur). Maintenant, le jeu est de trouver quatre points de la courbe qui forment un carré. Si tout va bien, vous devriez trouver. Sinon, c'est que vous avez mal cherché, ou que vous êtes tombé sur un contre-exemple (mais je miserais plutôt sur le fait que vous avez mal cherché)
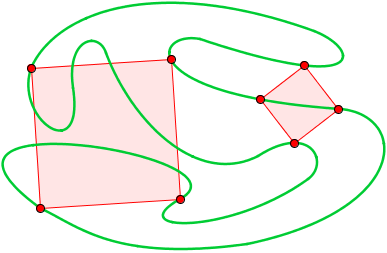
Exemple de courbe de Jordan possédant (au moins) deux carrés inscrits
Soyons précis dans les termes : une courbe de Jordan , c'est donc une courbe fermée sans point double. On dit qu'un polygone est inscrit dans la courbe si ses sommets tombent sur la courbe en question. La conjecture de Toeplitz demande donc :
Une courbe de Jordan admet-elle toujours un carré inscrit ?
On peut s'attendre à plusieurs réponses :
- Toutes ? Oui, sans exception !
- Toutes ? Non ! Mais la probabilité de trouver un contre-exemple en tirant au hasard dans l'ensemble des courbe est nulle.
- Toutes ? Loin de là ! La probabilité de trouver une courbe admettant un carré inscrit est nulle.
- Toutes ? N'importe quoi ! Aucune, plutôt !
Étant donné qu'il existe au moins un exemple, on peut oublier la dernière réponse, mais dans l'état actuel des choses, on ne sait pas trancher entre les trois réponses possible : on ne sait pas à quel point il existe des contre-exemple... Cela dit, un théorème particulièrement intéressant fait le buzz en 1989 : le théorème de Stromquist, qui répond à la conjecture de Toeplitz en disant :
Oui.
Ou, pour être plus précis, la courbe possède son carré inscrit si elle est suffisamment sympathique (dans le sens où elle ne doit pas avoir de comportement fractal). Le problème, c'est que l'ensemble des courbes sympathique ne représente qu'une infime partie de l'ensemble des courbes. Ce théorème répond quand même un peu au problème de départ, puisque si on dessine vraiment notre courbe sur un bout de papier, elle sera "suffisamment sympathique". Ce théorème répond donc à 99% à la question posée, mais le 1% demande encore beaucoup de travail...
Ou pourrais aussi penser à approcher une courbe quelconque par une suite de courbe sympathique en prenant à chaque fois le carré donné par le théorème de Stromquist, mais on n'est pas sûr d'obtenir un carré de côté non nul après le passage à la limite (et si on autorise ce genre de carré, la question n'a plus trop d'intérêt...)
Bref, ce problème est difficile, et fait appel à des considérations sophistiquées... Mais les variantes du problèmes sont bien plus faciles à résoudre, et demandent des solutions ingénieuses ! Voici donc ce qu'il se passe quand on considère les courbes symétriques, ou quand on cherche des parallélogrammes, des losanges ou des triangles inscrits.
Le problème du carré inscrit - dans une courbe symétrique
Comme le problème est difficile dans sa généralité, autant regarder un cas particulier. Le plus simple, c'est celui où la courbe J possède une symétrie centrale.

5 Carrés inscrits se cachent dans cette courbe de Jordan symétrique. Saurez-vous les débusquer ?
En deux coups de cuillère à pot, on peut trouver ses carrés inscrit. L'idée est de considérer la même figure après une rotation à 90° (R). Les deux courbes se coupent alors en au moins un point, disons P. Dans ce cas, les points P, -P, R(P) et -R(P) sont aussi sur la courbe en question, et forme un carré. CQFD !
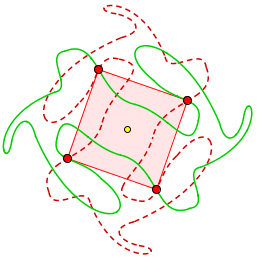
(En fait, non, il faut aussi montrer que les deux courbes se croisent bien quelque part. L'idée est de prendre deux points particuliers sur J - le plus proche et le plus éloigné du centre - et de montrer que leur image par R sont respectivement à l'intérieur et à l'extérieur du domaine délimité par J)
Le problème du carré losange inscrit
Changeons. Au lieu de chercher un carré, et si on cherchait plutôt un losange ? Ou un parallélogramme ? Nielson montre en 1995 qu'il existe toujours une infinité de losanges inscrits dans une courbe de Jordan, et il utilise pour cela une technique de preuve révolutionnaire : la preuve par "petits bonhomme qui gravissent une montagne" !
Notre courbe, on peut considérer que c'est un gros rocher posé en équilibre sur un sol horizontal. Quitte à faire basculer un peu le rocher, on peut supposer qu'il possède un seul sommet et qu'un seul point qui touche le sol. On considère donc 4 alpinistes : A, B, C et D. A et B partiront du sommet S du rocher et descendront en rappel, chacun de son côté du rocher. C et D, quant à eux, partiront de la base M du rocher, et grimperont.
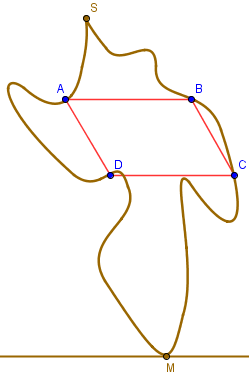
Ceci est une montagne, et les 4 points sont des alpinistes. Un peu d'imagination.
La descente, pour A et B ne se fait pas n'importe comment : ils font en sorte de toujours être à la même hauteur (et donc, [AB] est toujours parallèle au sol). Même si le relief ne se prête pas à une descente constante (par exemple, A devra remonter une fois au niveau du lac), les deux alpinistes peuvent toujours être à la même hauteur, quitte à ce que l'un d'eux rebrousse momentanément chemin.
C et D font la même chose, mais en partant de la base M du rocher, jusqu'à ce que A rencontre D et B rencontre C.
Mais les 4 alpinistes sont encore plus synchronisés que ça : ils font en sorte que la distance entre A et B soit toujours la même que celle entre C et D. Encore une fois, le terrain demandera sûrement à ce que l'un des deux couples fasse marche arrière pour que l'autre puisse progresser.
Grâce à tous ces efforts, les positions des 4 alpinistes forment en permanence un parallélogramme (où la direction horizontale a été arbitrairement choisie). Entre le moment où les alpinistes commencent leur descente/montée et le moment où ils se croisent, il y aura un instant où la distance entre les deux couples sera la même que la distance entre les deux alpinistes d'une même face. A ce moment très précis, ils formeront un losange. Celui que l'on recherche !
Le problème du carré triangle inscrit
Et pourquoi pas chercher un triangle inscrit ? Équilatéral, par exemple. Un théorème de 1980 nous dit qu'il en existe au moins un, et donne même une recette pour le trouver :
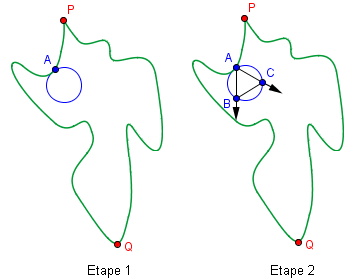
- Étape 1 : On considère un cercle à l'intérieur de la courbe J, et on le déplace jusqu'à ce qu'il entre en contacte avec la courbe en un point A. On considère aussi P et Q, deux points de J dont la distance est la plus grande possible
- Étape 2 : A partir de ce point A, on peut construire un triangle équilatéral ABC inscrit dans le cercle. On dilate le cercle jusqu'à ce que l'un des deux points (B ou C) rentre en contact avec la courbe.
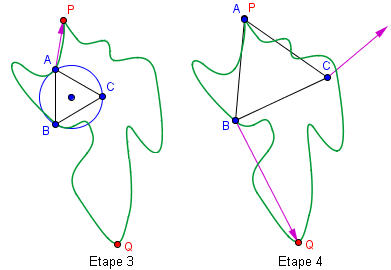
- Étape 3 : Disons que c'est le point B qui touche J en premier (si les deux le touche en même temps, on a trouvé le triangle qu'il fallait). C est donc à l'intérieur de J. En maintenant fixé le point B, on déplace A jusqu'en P, tout en gardant le triangle équilatéral. Si tout va bien, C sortira de J, et donc, croisera la courbe (ce qui donne un triangle ABC équilatéral).
- Étape 4 : Sinon, C est toujours à l'intérieur. Pas grave. On garde cette fois fixe le point A, et on déplace B jusqu'en Q. La distance PQ étant supposée maximale, le point C sortira de J, en le croisant, ce qui donne le triangle cherché.
En fait, cette preuve permet de trouver un triangle similaire à n'importe quel triangle donné. Dans la preuve, il faut cependant veiller à ce que AB soit le plus petit côté du triangle, pour être sûr que le troisième point sorte de la courbe à l'étape 4.
Cette version du théorème du triangle inscrit dit qu'il en existe au moins un, mais une version plus forte (démontrée en 1992) indique qu'il y en a une infinité et que, si on les dessine tous, l'intérieur de la courbe sera complètement colorié. On peut même montrer que le théorème reste vrai (moyennant une petite hypothèse) quand on considère la courbe dans l'espace plutôt que dans le plan. Pour ce qui est des dimensions supérieures, la question reste ouverte...
Sources :
Figures Inscribed in Curves, par Mark J. Nielson : un tour d'horizon encore plus large, avec les définitions et démonstrations un peu plus rigoureuses qui manquent à mon article, et le cas du rectangle inscrit que je n'ai même pas évoqué.



/http%3A%2F%2Fstorage.canalblog.com%2F77%2F73%2F210892%2F111515552_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F43%2F78%2F210892%2F106322231_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F16%2F78%2F210892%2F106207701_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F63%2F97%2F210892%2F99779882_o.png)