Ange ou démon ?
A quoi ressemble exactement la frontière entre le bien et le mal ? Qu'est ce qui sépare fondamentalement le froid du chaud ? Comment distinguer le sombre de la clarté ? Seuls trois mathématiciens chevronnés pouvaient s'attaquer à la résolution de ces mystères. Leur réponse est sans appel : c'est la spirale de Fermat !

Le tàijí tú : symbole de la dualité yīn-yáng
Les taoïstes me contrediront sûrement, mais le yin et le yang, c'est ce qui décrit comment les forces contraires de la nature sont interconnectées et interdépendantes. Elles apparaissent dans les écrits de Lao Tseu, au chapitre 42 du Tao Tö King. Sans doute par goût esthétique, Zhu Xi a popularisé le Taijitu, la représentation graphique bien connue du yin et du yang.
Oui, mais... Comment représenter au mieux ce Taijitu ? Quelle est la courbe qui sépare au mieux le yin du yang ? C'est la question que se sont posée Taras Banakh, Oleg Verbitsky et Yaroslav Vorobets (deux mathématiciens Ukrainiens et un Américain), avant de trouver une réponse en 2009.

Qui sera le meilleur yin-yang ?
Mais de quoi on parle ?
Il s'agit donc de trouver une courbe β (la courbe qui ressemble à un S) qui sépare le yin du yang de la manière la plus harmonieuse possible. Que doit-on attendre d'elle ? Les trois mathématiciens proposent 6 hypothèses, mêlant des arguments esthétiques et philosophiques.
A1 : β sépare D en deux parties identiques, D étant un disque d'aire 1 (ie., de rayon 1/√π)
Il ne faudrait quand même pas que le yin soit plus fort que le yang !
A2 : β traverse tout cercle concentrique à D exactement deux fois
Là, c'est par soucis d'esthétisme (ce qui oblige, au passage, β à passer par le centre du disque).
A3 : Tout rayon de D coupe β exactement une fois (ou 2, si on compte le centre)
C'est une hypothèse un peu plus discutable, mais c'est philosophiquement intéressant : tout rayon a une partie yin et une partie yang.
A5 : β est une courbe lisse
Déjà, parce que c'est plus joli comme ça, et surtout, ça évite tout un tas de cas dégénérés (Et personne ne voudrait d'un Taijitu dégénéré).
A6 : β possède des coordonnées polaires algébriques
Qui voudrait d'une frontière irrationnelle entre le yin et le yang ? L'équation de la courbe ne devra faire intervenir que des polynômes.
Avec ces 5 hypothèses, tout une famille de courbes se dégage : les spirales. Mais laquelle choisir : D'Archimède ? De Fermat ? D'or ? Logarithmique ?
L'hypothèse de la symétrie
Il faut donc une dernière hypothèse, assurant un équilibre entre symétrie et asymétrie.
A4 : β sépare D en deux ensembles parfaits
C'est la moindre des choses que le yin et le yang soient parfaits...
On va appeler "symétrique" un sous-ensemble B du disque qui est sa propre image par une symétrie d'axe un diamètre du disque. On peut "symétriser" un ensemble quelconque en prenant son intersection avec son image.
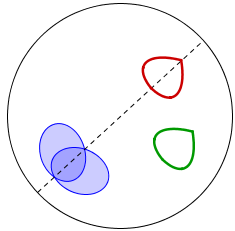
L'ensemble délimité par la courbe rouge est symétrique (dans le sens de l'article), contrairement à celui délimité par la courbe verte.
En intersectant l'ellipse bleu clair avec son image, on trouve un sous-ensemble (bleu foncé) symétrique.
On dit alors qu'un sous-ensemble A de D est parfait si son aire vaut 1/2 et que tout sous-ensemble symétrique de A a une aire d'au plus 1/4.
Non seulement, il existe des ensembles parfaits (c'est la moindre des choses), mais surtout, cette propriété possède un corollaire particulièrement intéressant : l'intersection entre un ensemble parfait et son symétrique par rapport à une droite a une aire valant toujours 1/4 (l'aire du symétrisé vaut la moitié de celle de l'ensemble parfait).

L'ensemble en rouge est parfait : l'aire de son sous-ensemble symétrisé (en violet) par rapport au diamètre vertical vaut la moitié de l'ensemble rouge. Un applet est disponible là-bas, pour faire tourner le diamètre.
L'hypothèse prend donc tout son sens : en demandant au yin (resp. le yang) d'être un ensemble parfait, on demande lui demande de posséder une dualité parfaite symétrie/asymétrie, et ce, dans tous les sens possibles. On ne peut pas mettre plus de dualité !
La courbe du Taijitu est donc...
La spirale de Fermat, d'équation polaire π²r²=θ ! ou, d'équation cartésienne [±√(t/π²).cos(t), ±√(t/π²).sin(t)]. Et c'est la seule courbe (à une rotation près) qui vérifie les 6 hypothèses. Telle est la conclusion Banakh, Verbitsky et Vorobets.
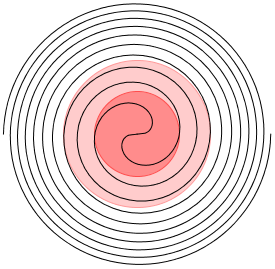
La spirale de Fermat. En prenant un cercle plus ou moins grand, on trouve plusieurs types de Taijitu.
Le coefficient π², c'est juste pour respecter l'hypothèse A3. En modifiant ce coefficient, on peut faire spiraler plus ou moins le Taijitu, et, par exemple, faire en sorte que chaque rayon coupe β exactement deux fois.
Et en vrai ?
Le symbole du yin-yang apparaît dans le drapeau sud-coréen, et donc, a déjà été normalisé. Plutôt qu'une spirale de Fermat, le choix s'est porté sur deux demi-cercles de rayon 1/2. Au moins, la courbe et le bord du cercle sont tangents.
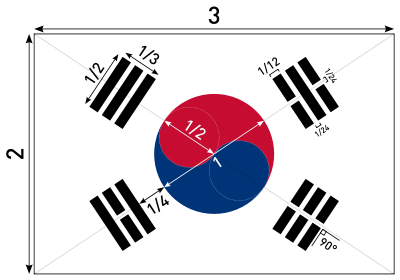
Les dimensions normalisées du drapeau de la Corée du Sud.
En remontant dans l'histoire des drapeaux du pays, on retrouve celui de 1882, featuring... une spirale de Fermat !

L'ancien drapeau de la Corée du Sud
Sources :
Le Yin et le Yang sur Images des mathématiques, article duquel je me suis (très) grandement inspiré.
Fermat's spiral and the line between Yin and Yang, l'article original de Banakh, Verbitsky et Vorobets.



/http%3A%2F%2Fstorage.canalblog.com%2F77%2F73%2F210892%2F111515552_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F43%2F78%2F210892%2F106322231_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F16%2F78%2F210892%2F106207701_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F63%2F97%2F210892%2F99779882_o.png)