Deux hommes d'exception
Le 25 mars dernier, le lauréat du prix Abel a été révélé et, pour une fois, ce n'est pas un mathématicien qui est récompensé du "prix Nobel des maths", mais deux : il s'agit de la rockstar John Nash, et du un peu moins célèbre Louis Nirenberg. Les deux ont été récompensés pour « leur contribution importante et fondamentale à la théorie des équations aux dérivées partielles non linéaires et leurs applications en analyse géométrique. »


John Forbes Nash Jr et Louis Nirenberg
D'un côté, il y a l'américain John Russell Crowe Nash, essentiellement célèbre pour avoir été l'un des rares mathématiciens récompensé d'un prix Nobel (même si le Nobel d'économie n'en est pas vraiment un...) pour ses travaux en théorie des jeux. Mais sa célébrité vient surtout de Hollywood, qui lui a consacré un biopic un brin romancé et multi oscarisé en 2001, avec Un homme d'exception (A beautiful mind). Le film met en scène ses années à Princeton, où il met au point le concept d'équilibre dans les jeux non-coopératifs, appelé aujourd'hui "équilibre de Nash" (faudrait que j'écrive un article là-dessus un de ces jours...). Mais ce que Hollywood met surtout en scène, ce sont les 30 années (de 1959 à 1990) où il est dans l'incapacité de faire des mathématiques à cause de la schizophrénie paranoïque qui lui a été diagnostiqué. Le film passe cependant à côté de ce qui fait sa renommée dans le monde des mathématiques, ses travaux en analyse géométrique, qui lui vaut aujourd'hui l'une des deux récompenses suprêmes pour un mathématicien.
De l'autre côté, il y a le canado-américain Louis Nirenberg, avec un parcours forcément un peu plus classique. Il fait sa thèse à l'Université de New York (NYU) à partir de 1947 sous la direction de James Stocker qui lui propose un problème de géométrie ouvert depuis 30 ans, le problème de Weyl. Ce problème qui traite de sphère, il l'attaque sous l'angle original des équations aux dérivées partielles (EDP) elliptiques, sujet qu'il traitera sous toutes ses formes jusqu'à sa retraite en 1999, et toujours au NYU. Bien que 90% des papiers qu'il ait rédigé soient en collaboration avec d'autres mathématiciens, il n'en a jamais cosigné avec John Nash. Il se sont cependant rencontrés à la fin des années 50, où Nirenberg lui a exposé un problème concernant les EDP qui deviendra quelques années plus tard le théorème de De Giorgi-Nash-Moser.
Analyse géométrique
L'analyse géométrique, c'est donc la branche des mathématiques qui s'occupe de traiter les problèmes de géométrie (sur la forme et la mesure d'objets comme des courbes ou des surfaces) avec les outils des analystes, notamment les EDP (sans rentrer dans les détails, une EDP est une équation où les inconnues sont des fonctions à plusieurs variables -- le simple fait de montrer qu'une telle équation admet une solution est en général particulièrement difficile...)
Le problème récurrent de ce domaine est celui des plongements, et plus particulièrement celui des plongements isométriques. Comme son nom l'indique, un plongement est l'opération qui consiste à placer un objet géométrique dans un espace donné.
Prenons l'exemple du tore. Sa représentation habituelle est celle de la surface d'un donut's ou d'une bouée, une représentation qui n'existe donc que dans un espace à trois dimensions. L'image que l'on se fait d'un tore est donc le plongement de celui-ci dans l'espace R3.

Plongement d'un tore dans l'espace euclidien R3
Mais le tore est une surface, un objet à seulement deux dimensions : il n'a a priori pas besoin d'un espace à 3 dimensions pour exister. Et c'est bien le cas, on peut se représenter un tore à l'extérieur d'un espace tridimentionnel, en prenant l'image du jeu vidéo Asteroids : un carré où les côtés opposés sont identifiés, c'est à dire que, lorsque l'on quitte ce carré du côté droit, on réapparait du gauche, et réciproquement ; même chose pour les bords hauts et bas.
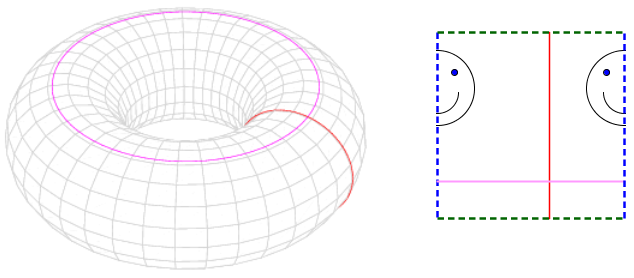
Les deux représentations les plus communes d'un tore.
Sur le carré-tore de droite, les flèches bleues et vertes se correspondent.
Le parallèle rose et le méridien rouge du 3D correspondent aux paires de flèches du tore carré.
Pour ce tore carré, le plongement dans l'espace 3D le plus simple est de procéder par origami. On commence par enrouler le carré pour faire correspondre les côtés droit et gauche (on obtient un cylindre), puis, on enroule ce cylindre de façon à faire correspondre les bords haut et bas (bon, il faut imaginer ce papier élastique pour pouvoir réaliser cette opération). Un soucis subsiste : quand on passe de cette façon d'un tore plat à un tore en volume, on doit mettre de côté l'aspect géométrique. Si le plongement s'était mieux passé, les cercles rose et rouge sur le carré-tore auraient été de longueurs identiques sur le beignet-tore. L'idéal, ça serait un plongement qui respecte les longueurs.
Mais existe-t-il vraiment un moyen de représenter un tore en 3D tout en gardant les longueurs de départ ? C'est ce que l'on appelle le problème du plongement isométrique, et c'est celui-ci que Nash a résolu en transformant ce problème de géométrie en problème d'analyse.
Problème du plongement isométrique (un théorème de Nash)
En fait, la question ne porte pas exclusivement sur les tores, mais sur n'importe quelle courbe ou autres surfaces et espaces de dimension supérieur (plus particulièrement, les variétés riemaniennes). La question du simple plongement a été réglée depuis longtemps : il y a toujours moyen de se représenter ces objets dans l'espace euclidien auquel on est habitué.
Le problème, c'est que dans l'espace euclidien, on a une façon habituelle de mesurer les distances (mesure euclidienne avec une bonne vieille règle graduée, toussa), et qu'il est hors de question de changer notre façon de mesurer les distances sous prétexte que l'objet géométrique sur lequel on travaille vient d'un espace topologique exotique sur lequel on ne mesure pas les distances de la même façon. En fait, une variété riemanienne, c'est ça : un espace topologique (une courbe, une surface) qui dispose de sa propre façon d'y mesurer les distances. Et un plongement isométrique, c'est un plongement de cette variété dans l'espace euclidien où la distance euclidienne coïncide avec la distance propre à la variété.
Prenons l'exemple d'une variété riemanienne assez simple de dimension 1 : une route de campagne, rectiligne, sur lequel nous marchons. La particularité de cette route, c'est que plus on y progresse, plus elle devient boueuse, et donc, plus notre marche devient lente. Pour mesurer des distances entre deux points de cette route, la façon habituelle de mesurer ("il y a 5 km entre le point A et le point B") n'est pas adaptée, il serait plus logique de les mesurer en temps ("il y a une heure entre le point A et le point B").
Le problème, c'est que si on regarde cette route d'un point de vue extérieur, la mesure temporelle ne coïncide pas du tout avec la mesure à vol d'oiseau. Le plongement de cette route dans l'espace euclidien n'est donc pas isométrique. Y a-t-il moyen de représenter cette route sur un plan de façon à ce que la mesure temporelle et la mesure euclidienne soit la même ?
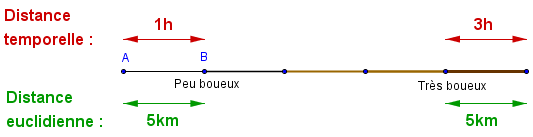
Plongement de la variété "route boueuse" dans l'espace euclidien :
la distance intrinsèque de la variété (la distance temporelle) ne correspond pas à la distance euclidienne.
Une façon simple de contourner le problème est de représenter la route en la dilatant de façon à ce que 5km sur le plan correspondent toujours à une heure sur la route. Le problème, c'est que la représentation que l'on obtient au final est très éloignée de la route initiale.

Plongement de la variété "route boueuse" dans l'espace euclidien :
la distance intrinsèque de la variété (la distance temporelle) correspond à la distance euclidienne.
Le résultat est cependant éloigné du plongement initial.
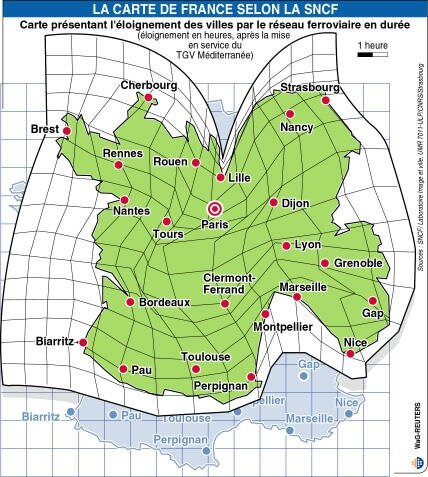
C'est ce principe que l'on utilise pour faire des cartes temporelles, où la distance euclidienne correspond à la distance temporelle :
Oui, mais ce que l'on veut, c'est le beurre et l'argent du beurre : une représentation de cette route boueuse où la distance euclidienne soit égale au temps de parcours et qui, en plus, ne soit pas trop éloignée de la représentation initiale.
Aussi étonnant que cela puisse paraître, c'est parfaitement possible ! Et si personne n'y avait pensé avant Nash, c'est parce que le résultat défie l'intuition :

En ajoutant des oscillations, les distances temporelles et euclidiennes se correspondent, et le résultat est proche de la représentation initiale. C'est le plongement parfait !
Imaginons un vélo où les pédales feraient tourner les deux roues en même temps, mais où l'une des roues tournerait plus vite que l'autre. Pour faire avancer ce vélo sans déraper, il faut nécéssairement que les trajectoires des roues soient proches l'une de l'autre, mais que l'une des deux trajectoires soit plus longue que l'autre. La trajectoire de la roue plus rapide sera nécéssairement pleine d'ondulations, pour compenser la différence de vitesse. C'est exactement la même chose qu'il s'est passé dans cette histoire de plongement isométrique de route boueuse.
On peut se poser la même question pour le tore carré présenté plus haut. A partir d'un carré de papier non élastique, peut-on le déformer sans plis ni déchirement de façon à obtenir un tore ?... D'après Nash, oui, un tel un plongement existe. Autant le raisonnement est a peu près accessible pour des objets à une seule dimension comme un route, autant la généralisation aux surfaces ou aux variétés riemaniennes de dimensions supérieures devient un casse-tête pour l'intuition. La complexité des arguments du théorème de Nash-Kuiper publié en 1954 fait qu'il a fallu attendre 2012 pour ce donner une idée de ce que cela pourrait donner (j'en avais parlé ici).

Plongement isométrique d'un tore : forcément, il est plein d'ondulations
Problème de Minkovski (un théorème de Nirenberg)
Un petit mot sur un des premiers problèmes auquel Nirenberg s'est attaqué en 1953 : le problème de Minkovski.
Pour comprendre la question, il faut parler de courbure, qui permet de quantifier à quel point un objet est courbe.
Grosso modo, la courbure d'un arc correspond à l'inverse du rayon du cercle qui ajuste au mieux cette courbe (le cercle osculateur, littéralement, "qui donne un baiser"). Ainsi, si une courbe présente un virage dur, le cercle osculateur sera petit, et donc, sa courbure grande. Inversement, si une courbe présente un virage faible, le cercle osculateur sera grand, et donc la courbure faible. Une courbure nulle correspond à une courbe localement très plate.
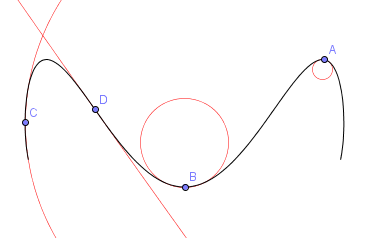
Une courbe et quelques cercles osculateurs.
La courbure en A est donc grande tandis que la courbure en C est faible (et intermédiaire en B)
Au point D, le cercle osculateur a un rayon infini, la courbure y est donc nulle.
On peut alors se demander à quoi ressemblerait une courbe dont la courbure en tout point serait fixée à l'avance.
Par exemple, à quoi ressemble une courbe dont la courbure serait en tout point égale à son abscisse curviligne (autrement dit, une courbe où, plus on avance dessus, plus la courbure devient grande). Eh bien, cela donne la clothoïde (du grec klothein : filer la laine), une courbe particulièrement utilisée dans le design des autoroutes ou des chemins de fer :
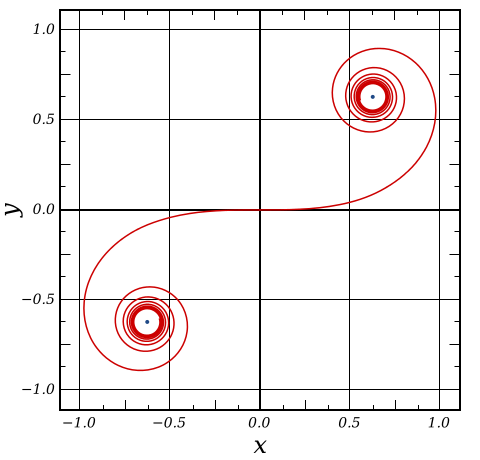
La clothoïde, courbe qui correspond à la trajectoire d'une voiture où le conducteur tourne le volant à vitesse constante.
En avançant à vitesse constante sur une telle courbe, la force centrifuge subie sera proportionelle au temps, d'où son utilisation dans les bretelles d'autoroute.
La même question se pose pour les surfaces où l'on peut aussi y définir une courbure particulière, la courbure de Gauss, dont la définition généralise celle de la courbure d'un arc.
Une sphère de rayon R a, en tout point, une courbure de Gauss égale à 1/R². Un plan, un cylindre ou un cône auront en tout point une courbure nulle (on peut toujours y trouver des plans de coupe rectiligne).
Bref. À quoi ressemblerait une surface dont la courbure en tout point serait une fonction (positive) définie à l'avance ? Tel est l'objet du problème posé en 1903 par Hermann Minkovski.
Prenons comme exemple la surface de la Terre. On peut prendre comme fonction la température moyenne en chaque point de la Terre (moyennant une renormalisation). On peut alors se demander à quoi ressemblerait cette Terre si en tout point, sa courbure était égale à la fonction. Cela donnerait donc un globe aplati au niveau des pôles (de courbure faible ) et bombés au niveau de l'équateur.
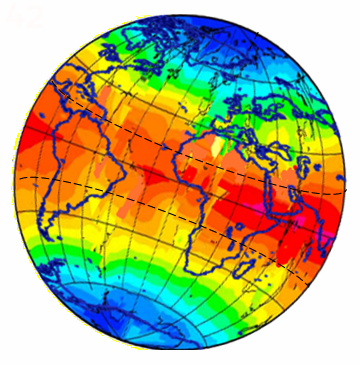
Un exemple de fonction définie sur une sphère.
Nirenberg a donc réussi à prouver que, sous les bonnes conditions, cette surface de courbure imposée existe toujours. Dans le même papier, il balaie une autre conjecture ouverte depuis 1916, la conjecture de Weyl. Sa solution marque un point important dans l'histoire de la géométrie puisque, pour la première fois, des problèmes de géométrie sont résolus à l'aide d'EDP non linéaires.
Sources :
John F. Nash Jr. and Louis Nirenberg, sur le site officiel du prix Abel
Images : photo 1, photo 2



/http%3A%2F%2Fstorage.canalblog.com%2F39%2F29%2F210892%2F122373793_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F84%2F61%2F210892%2F116475097_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F74%2F79%2F210892%2F116430959_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F72%2F92%2F210892%2F113119539_o.png)