Finistère amer
Ce soir, c'est crêpes party ! Une soirée conviviale et bon enfant où nous dégusterons ensemble de délicieuses crêpes à la mode bretonne !
Daou ha daou-ugent krampouezh
Entrées : farine, lait, oeufs (telles que les quantités appartiennent à l'enveloppe convexe des recettes acceptables de pâte à crêpe), sucre (parce que c'est meilleur) et un ingrédient secret (rhum, cognac, bière, fleur d'oranger, épice à pain d'épice, gouda, ...)
Sortie : de délicieuses crêpes
Algorithme :
: Mélanger le tout, puis laisser reposer la pâte.
: ???
: Profit !
Mais attention à ne pas négliger le plus important : le dressage ! Des crêpes, ça ne s'empile pas à la va-vite, il faut respecter une certaine harmonie quand on les superpose, de la plus grande à la plus petite !
Le problème des pancakes, par le mec devenu le plus riche au monde en vendant des logiciels
Pour trier des données, les informaticiens ont inventé un grand nombre d'algorithmes, plus ou moins efficaces : tri à bulles, tri par insertion, tri rapide, tri fusion, tri stupide, tri spaghetti... Mais ces méthodes de tri ne fonctionnent pas lorsque l'on doit trier une pile de crêpes (ou de pancake, pour les non breton-friendly) : des crêpes, ça ne s'échange pas, ça se retourne !
Le problème des crêpes est donc le suivant : vous êtes livreur de crêpes et vous travaillez pour le compte d'un crêpier renommé. Votre chef a cependant une très mauvaise habitude, ses crêpes sont de taille variable, et il les empile au fur et à mesure qu'elles arrivent. Avant de les apporter à vos clients, vous devez donc les trier, de la plus grande à la plus petite. Pour cela, vous ne disposez que d'une simple spatule. En la glissant entre deux crêpes, vous pouvez retourner le haut de la pile ; c'est la seule opération que vous pouvez faire pour réordonner votre tas de crêpes. Au pire, combien d'opérations (que l'on notera f(n)) seront nécessaires pour ranger complètement un tas de n crêpes ?
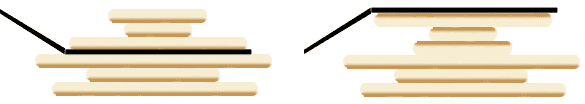La seule opération permise est de retourner à la spatule un certain nombre de crêpes au sommet de la pile.
Le problème a été proposé en 1975 par Harry Dweighter dans les pages de l'American Mathematical Monthly. Aucune solution n'est alors proposée, seulement quelques résultats obtenues à la main pour n petit. Il trouve par exemple que f(2)=1 ou f(7)=8 (OEIS : A058986). Si cette histoire de pancakes est aujourd'hui célèbre, c'est surtout parce qu'un certain William H. Gates (avec Christos H. Papadimitriou) s'intéresse à la question en 1979 dans un papier de Discrete Mathematics. Ils prouvent que 17n/16 ≤ f(n) ≤ (5n+5)/3. Ça sera le seul article écrit par Bill Gates avant qu'il invente Windows et devienne l'homme le plus riche au monde.
f(n) existe
Avant de chercher la meilleur solution, il faut au moins prouver qu'une solution existe. Utilisons le langage des permutations : puisque les transpositions élémentaires engendrent l'ensemble des permutations, il suffit de montrer qu'il est toujours possible d'échanger la place de deux crêpes adjacentes dans la pile.
Pour cela, appellons Mk l'opération qui consiste à glisser sa spatule sous la k-ième crêpe (en partant du haut), puis de retourner le haut de la pile. On peut alors montrer que pour échanger les crêpes n°k et k+1, il suffit de faire successivement les opérations Mk, Mk+1, Mk et Mk-1 :
Pour échanger la 4e et 5e crêpe, on effectue successivement les retournements M4, M5, M4 et M3.
Chaque transposition demande donc 4 opérations. On peut donc estimer à 16n2 le nombre de retournements à effectuer pour trier l'ensemble des crêpes (avec le tri à bulles). L'estimation est haute, on peut facilement améliorer ce résultat.
f(n) ≤ 2n-3 : algorithme simple
Il existe en fait un algorithme plutôt simple pour trier ses crêpes. Dans le pire des cas, cela demandera 2n-3 opérations. Le principe, c'est d'amener à sa place (au plus près de l'assiette) la plus grande des crêpes, puis de continuer avec la deuxième crêpe la plus grande, et ainsi de suite.
Dans la pratique :
- on repère la plus grande des crêpes non déjà triée. (disons que l'on cherche à amener la k-ième crêpe à la position i)
- on l'amène au sommet de la pile par un premier retournement (Mk)
- on l'amène à sa place par un deuxième retournement (Mi)
Ceci donne 2 opérations pour chacune des crêpes. Sachant que les deux dernières crêpe demanderont au pire une opération, on a le compte : 2n-3.
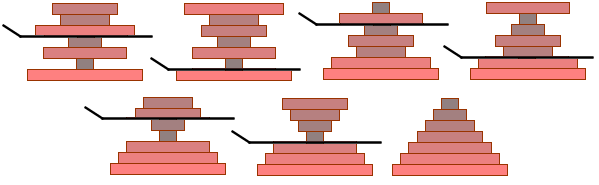
En suivant l'algorithme, on peut ranger ces 7 crêpes en seulement 6 retournements.
Vous pouvez voir l'algorithme en action dans cette vidéo.
f(n) ≤ 5/3 n + 5/3 : l'algorithme de Gates
Alors que l'algorithme simple consiste à ranger les crêpes en partant de la base de la pile, l'algorithme de Gates cherche à créer des blocs de crêpes rangées. Quand toutes les crêpes appartiennent au même bloc, c'est qu'elles sont complètement triées.
Il existe donc deux type de crêpes : celles qui sont libres et celles qui appartiennent à un bloc. On dira qu'une succession de crêpes forme un bloc quand elles y sont rangées (par ordre croissant ou décroissant). Si une crêpe n'appartient pas à un bloc, elle sera dite "libre".
On regarde alors la première crêpe de la pile, notée t. On notera t+o une crêpe immédiatement plus grande ou plus petite que t (o désigne en fait 1 ou -1). Il y a alors huit possibilités (liste exhaustive) :
- t est libre, t+o aussi. (cas a - 1 opération)
- t est libre, t+o est le premier élément d'un bloc. (cas b - 4 opérations)
- t est libre, t+o et t-o sont chacun le dernier élément d'un bloc. (cas c - 1 opération)
- t est dans un bloc, t+o est libre. (cas d - 1 opération)
- t est dans un bloc, t+o est le premier élément d'un bloc. (cas e - 1 opération)
- t est dans un bloc de longueur k+1, t-o est le dernier élément d'un bloc et t+(k+1).o est libre. (cas f et g - 4 opérations)
- t est dans un bloc de longueur k+1, t-o est le dernier élément d'un bloc et t+(k+1).o est dans un bloc. (cas h et k - 2 opérations)
- t est dans un bloc de longueur n.
Si on se trouve dans le dernier cas, c'est que les crêpes sont rangées. Sinon, on effectue une suite de mouvements en fonction de la situation. (Voir ici les différents mouvements). À chaque itération, la longueur des blocs augmente : l'algorithme se terminera forcément. Une analyse plus fine montre qu'il faudra au plus (5n+5)/3 opérations.
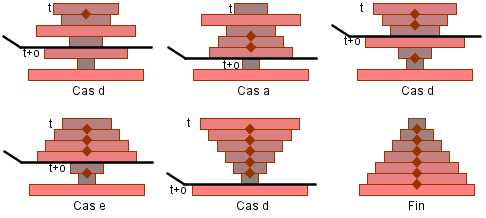
Application de l'algorithme : les 7 crêpes sont triées en seulement 5 opérations (seuls les cas a, d et e sont rencontrés)
L'algorithme de Gates et Papadimitriou sera amélioré en 2009 par une équipe de chercheurs américains. Le nombre d'opération nécéssaire pour trier n crêpes sera dans le pire de l'ordre de 18/11 n.
Le problème des pancakes cramés, par le mec qui a fait un dessin animé avec une cyclope sexy et un robot alcoolique
Il existe une variante du problème des pancakes : celui des pancakes cramés. Dans ce nouveau problème, l'une des faces de chacune des crêpes est brûlée. Dans l'empilement final, aucune de ces faces ne doit apparaître. La question reste la même : dans le pire des cas, quel est le nombre g(n) de retournements à effectuer pour ranger notre pile de crêpes ?
g(n) ≤ 3n-2
Pour ranger nos crêpes cramées, on peut reprendre l'algorithme simple en ajoutant l'étape qui consiste à retourner la crêpe la plus haute si nécéssaire. Ceci donne un nombre d'opérations proportionnel à 3n. Encore une fois, cette borne supérieure est améliorable.
g(n) ≤ 2n
Si le problème des pancakes doit sa renommée à Bill Gates, celui des pancakes cramés doit la sienne à David S. Cohen (appellé aujourd'hui David X. Cohen pour ajouter un effet SF), co-créateur de la série Futurama (une série bourrée de références mathématiques). Dans un papier publié en 1993 dans Discrete Applied Mathematics, il prouve, avec Manuel Blum, l'encadrement 3/2 n ≤ g(n) ≤ 2n - 2.
L'algorithme suit le même principe que celui de Gates : former des blocs, sous la contrainte qu'au sein de ce bloc, une face brûlée doit toujours être en contact avec la face non-brûlée de la crêpe qui suit. Chaque itération de l'algorithme (qui demande à chaque fois deux opérations) consiste alors à augmenter la taille de ces blocs.
Dans la pratique, deux cas se présentent :
- Au moins une crêpe est dans le bon sens. Supposons que la plus grande d'entre elles est en position k :
-- si c'est la plus grande des crêpes, on l'amènera au bas de la pile (cas a : Mk puis Mn).
-- sinon, il existe une crêpe à l'envers immédiatement plus grande, en position l. On collera ces deux crêpes (cas b : Ml puis Mk'-1 si l>k ; cas c Mk puis Ml'-1 sinon).
- Toutes les crêpes sont à l'envers :
-- Si elles sont complètement rangées, on effectuera n fois les opérations Mn puis Mn-1 (cas *).
-- Sinon, il existe au moins deux crêpes (en position l et k) non collées et non ordonnées que l'on peut réunir en deux opérations (cas d : Ml puis Mk'-1).
À chaque étape (sauf dans le cas *), le nombre de crêpes à considérer diminue (soient elles sont collées - elles comptent comme une seule crêpe, soit elle sont rangées dans le bon ordre depuis l'assiette - on ne les prendra plus en compte).
Ces 7 crêpes sont rangées en 9 retournements.
Au final, cet algorithme rangera les n crêpes en au plus 2n retournements. En l'améliorant un peu, il est possible de gagner deux opérations.
Les deux problèmes restent à l'heure actuelle toujours ouverts. Les calculs ont été menés jusqu'à n=17 (ce qui donne tout de même 17!=3.5×1014 configurations à analyser !) : il faut au maximum 19 retournements pour trier 17 crêpes. Le problème des pancakes brûlés n'a été étudié que jusqu'à n=12 (12!×212=2×1012 configurations possibles) : il faudra au maximum 21 mouvements.
La principale question ouverte reste cependant la suivante : quand on est un vrai Breton, doit-on mettre du sucre dans la pâte à crêpe ?
Sources :
Stack of pancakes, Harry Dweighter, The American Mathematical Monthly Vol. 84, No. 4
Bounds for Sorting by Prefix Reversal, William H. Gates et Christos H. Papadimitriou, Discrete Mathematics 27
On the problem of sorting burnt pancakes, David S. Cohen et Manuel Blum, Discrete Applied Mathematics 61
Images :
Crêpes
/http%3A%2F%2Fstorage.canalblog.com%2F78%2F22%2F210892%2F100064815_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F71%2F58%2F210892%2F80030823_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F23%2F91%2F210892%2F62233403_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F17%2F70%2F210892%2F62007684_o.png)
