J'ai toujours rêvé d'être acarreleur
L'Académie royale des sciences de Suède n'a toujours pas décerné de prix Nobel en mathématiques. Par contre, le prix Nobel de chimie a été remis à l’Israélien Daniel Shechtman pour sa découverte des quasi-cristaux en 1982. Pour moi qui ai toujours rêvé d'être carreleur, c'est l'occasion où jamais de reparler de pavages.
Pavages périodiques
Dans un cristal, les atomes sont bien rangés, et suivent des motifs simples. Ce rangement est périodique : c'est la même maille (le même motif) qui est répété dans l'ensemble du matériau. Pour cela, ce motif doit suivre certaines règles : des règles de symétries. Alors, les motifs aptes à paver le plan doivent présenter des symétries d'ordre 2, 3, 4 ou 6 (l'ordre d'une symétrie est le nombre de fois qu'il faut la répéter pour revenir au point de départ). Les motifs à symétries d'ordre 5, 7 ou plus sont priées d'aller voir ailleurs.
Par exemple, on peut paver le plan avec des rectangles (symétrie d'ordre 2), des triangles équilatéraux (d'ordre 3), des carrés (d'ordre 4) ou des hexagones (d'ordre 6). Avec des pentagones (ordre 5), c'est totalement impossible).

Paver le plan avec des triangles, des carrés ou des hexagones : c'est possible !
Les cristaux, c'est la même chose en 3 dimensions : il est impossible de trouver des symétries d'ordre 5 ou d'ordre 10.
Pavages quasi-périodiques
Mais ça, c'était avant le drame, avant le matin du 8 avril 1982. C'était un jeudi. Daniel Shechtman, de l'Institut israélien de technologie, s'amuse à diffracter des électrons à travers un alliage d'aluminium et de manganèse (les chimistes font souvent ce genre de choses pour comprendre l'arrangement des atomes), et découvre que celui-ci présente une symétrie d'ordre 10 ! "Impossible", se dit-il. Il en parle alors à ses collègues qui lui disent également qu'il a dû se tromper quelque part. Après quelques années, ses résultats ont finalement été pris au sérieux, et des collègues chimistes lui ont avoué qu'ils avaient déjà découvert des symétries d'ordre impossible dans des cristaux, mais qu'ils avaient préféré conclure à une erreur expérimentale.
C'est ainsi que les quasi-cristaux (cristaux quasi-périodiques) ont été découverts.
En fait, les bases théoriques des quasi-cristaux existaient déjà dans la littérature mathématique depuis les années 70, avec les pavages quasi-périodiques. Bien que définis rigoureusement, ceux-ci ne présentent aucune périodicité, contrairement aux 17 types de pavages périodiques (stables selon plusieurs translations). Le plus célèbre pavage pseudo-périodique est le pavage de Penrose.
Petite parenthèse : la cristallographie mathématique regorge de termes aux sens plus ou moins proches comme les pavages "apériodiques", "non-périodiques", "pseudo-périodiques". Ne comptez pas sur moi pour vous l'expliquer ici, ce n'est pas l'endroit pour ça.
En 1977, donc, Roger Penrose, physicien anglais, découvre que l'on peut paver le plan avec un couple de motifs, les "tuiles de Penrose". Avec les tuiles "cerf-volant" et les tuiles "flèche", on peut, en suivant scrupuleusement le mode d'emploi, remplir l'espace de motifs transpirant le nombre d'or (comme tout ce qui présente des symétries d'ordre 5).
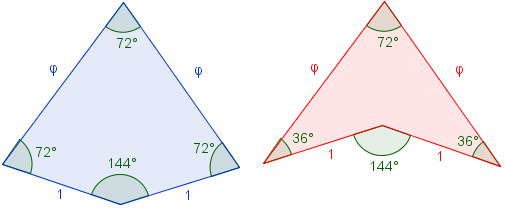
La tuile "cerf-volant" et la tuile "flèche", construites à partir du nombre d'or.
Pour cela, on part de la figure du Soleil (un décagone régulier formé par 5 cerf-volants), et on applique pour chaque pièce les transformations suivantes :

Les deux transformations de Penrose
En réitérant le processus, on obtient un pavage de plus en plus complexe. Après 5 étapes, on retrouve le motif du Soleil.
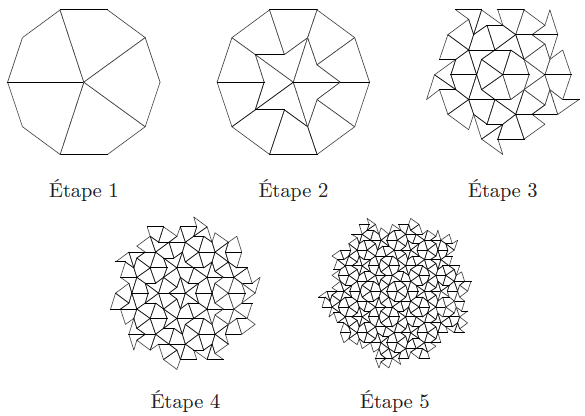
Les cinq premières étapes d'un pavage de Penrose
Avec une homothétie, on peut alors revenir à la configuration du départ et donc, paver le plan.

Le pavage de Penrose est vraiment très joli.
Le pavage de Penrose est typiquement le genre de configuration qui donne à un cristal une structure possédant une symétrie d'ordre 5...
Pavages apériodiques
En fait, le pavage cerf-volant + flèche n'est que le deuxième des trois pavages de Penrose. Quelques années plus tôt, il avait déjà trouvé que l'on pouvait paver le plan avec 4 tuiles : des pentagones réguliers, des pentagrammes réguliers (étoile à 5 branches), des "bateaux" (3/5 d'un pentagramme) et des losanges. Le résultat est lui aussi très joli (et très apériodique) :
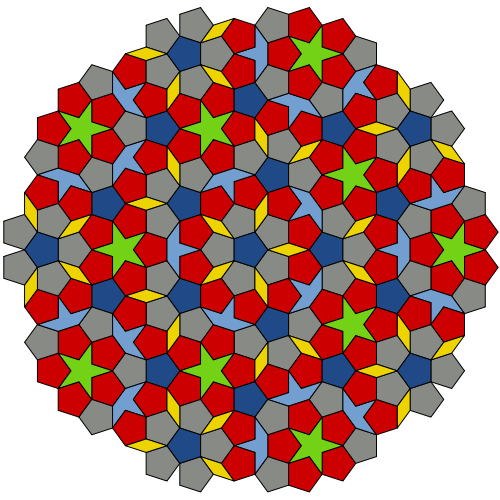
Le pavage de Penrose de type 1 est vraiment très joli.
Je dois également évoquer le pavage de Penrose de type 3, mélangeant deux types de losanges :

Le pavage de type 3 de Penrose est lui aussi très joli.
Et histoire de finir en beauté, le pavage pinwheel (lui aussi, pas du tout périodique) de John Conway (encore lui). Il est construit à partir d'une unique tuile rectangle (rectangle droit de côtés 1, 2 et √5) que l'on retrouve dans un nombre infini de directions différentes. Et pourtant, il est parfaitement défini, sans aucune ambiguïté (pas de recours au hasard, par exemple).

Le pavage pinwheel est lui aussi très... intéressant !
Sources :
Pavages périodiques, Vincent Pilaud, où j'ai récupéré l'illustration des premières étapes du pavage de Penrose
Pour le reste, wikipédia a bien bossé (ici la liste de tous les pavages apériodiques)



/http%3A%2F%2Fstorage.canalblog.com%2F77%2F73%2F210892%2F111515552_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F43%2F78%2F210892%2F106322231_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F16%2F78%2F210892%2F106207701_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F63%2F97%2F210892%2F99779882_o.png)