Made in Sinaï

Le prix Abel 2014 a été annoncé le 26 mars dernier, et l'heureux lauréat est russe ! C'est donc le mathématicien (et un peu physicien) Iakov Sinaï qui décroche cette année le prix Nobel des maths (parce que, non, la médaille Fields n'est pas l'équivalent d'un Nobel, c'est encore plus prestigieux). Il est récompensé pour l'ensemble de son œuvre : des travaux sur les systèmes dynamiques, sur la théorie ergodique et en physique mathématique. Son nom restera surtout associé aux systèmes dynamiques, grâce au billard de Sinaï et à l'entropie de Sinaï-Kolmogorov. A quoi ressemblent ces bêtes là ? Quelques éléments de réponse.

Iakov (Yakov ?!) Sinaï

Le billard de Sinaï
On appelle système dynamique un processus évoluant au cours du temps qui ne fait absolument pas intervenir le hasard (autrement dit, déterministe). L'objet préféré des gens qui étudient les systèmes dynamiques, c'est le billard. Enfin, pas n'importe quel billard : un billard sans trou et qui se joue avec une seule boule (infiniment fine). Une fois lancée, la boule ne s'arrête plus, et suit les loi de la physique lorsqu'elle rebondit sur les parois. En fait, le billard des mathématicien est surtout une façon simple de modéliser le comportement d'un particule d'un gaz.

Dans un tel billard, une fois que l'on connaît la position précise de la balle et sa direction initiale, les lois de la physique nous permettent de prédire avec exactitude la trajectoire qu'elle suivra. Cette trajectoire est donc parfaitement déterministe.

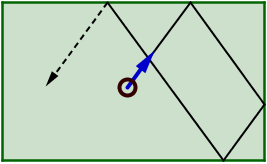
Je lance ma boule selon la direction bleue : elle rebondit, tout est normal.

Si je modifie un peu la position ou la direction initiale de la balle, la trajectoire change. Mais pas tant que ça. En déplaçant la balle et en conservant la même direction, la balle aura une trajectoire parallèle à sa trajectoire initiale ; si c'est la direction que l'on change, la balle déviera de plus en plus de sa trajectoire initiale avec le temps, mais rien de très inquiétant.

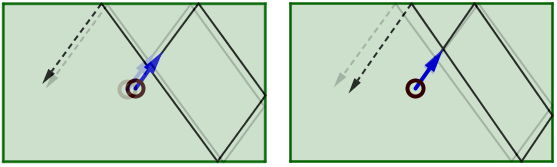
à gauche, un changement de position initiale
à droite, un changement de direction initiale
De petits changements entraînent de petites déviations

Par contre, quand Sinaï joue au billard, il n'hésite pas à rajouter un gros cylindre en plein milieu de sa table. La physique permet toujours de prédire la trajectoire de la balle, ce système dynamique est toujours parfaitement déterministe.

Le véritable "billard de Sinaï" est carré, mais l'idée est la même

La grosse différence d'avec le premier billard, c'est que la trajectoire devient difficile à prévoir lorsque l'on modifie un peu les conditions initiales. En déplaçant, même légèrement, la position de départ de la balle, la trajectoire devient très rapidement complètement différente. Même remarque si l'on modifie un peu sa direction.

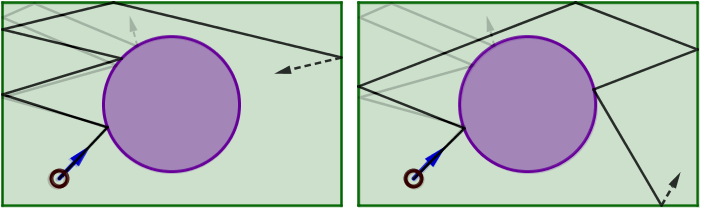
Avec un petit changement des conditions initiales, la trajectoire change du tout au tout.

Bien que les trajectoires soient complètement prévisible, puisque déterministe, il est en fait impossible de les prévoir sans passer par l'essai. On peut alors qualifier ces trajectoires comme "chaotique" : une petite modification des conditions initiales change très rapidement l'aspect global de la trajectoire. Il existe de très nombreux exemple de systèmes chaotiques, je vous invite plutôt à écouter le dernier épisode de Podcast Science sur le sujet.

Assez paradoxalement, bien qu'il soit impossible de prévoir le comportement d'une trajectoire sans connaître précisément ses conditions initiales, il est quand même possible d'y prévoir des choses. Par exemple, (sauf cas particuliers), les trajectoires seront ergodiques : si on choisit un point sur le bord du billard, la balle finira forcément par passer à un moment ou à un autre près de ce point (et même, aussi près de ce point que l'on veut, si l'on accepte d'attendre longtemps).

Sinaï a en fait produit cet exemple de billard pour montrer qu'il existe un système qui soit à la fois chaotique ("d'exposant de Lyapounov positif") et ergodique, dans le cadre d'un problème sur le comportement physique du mouvement de gaz.

L'entropie de Sinaï-Kolmogorov
Finalement, certains systèmes dynamiques sont faciles à prévoir à court comme à long terme, d'autres le sont à court terme mais pas à long terme, d'autres encore ne le sont plus à moyen terme... Il faut trouver quelque chose pour mesurer tout ça ; ce quelque chose, c'est l'entropie.

Cette entropie n'a pas de rapport direct avec l'entropie des physiciens, mais plutôt avec celle des théoriciens de l'information, à travers l'entropie de Shannon. La définition de l'entropie de Shannon permet de dire qu'une suite de caractère possédant une forte entropie est riche en informations.

Par exemple, les deux phrases "six fois sept égale quarante-deux" et "6×7=42" apportent exactement la même information, mais la deuxième compte sensiblement moins de caractère que la première. La quantité d'information par caractère contenu dans la première phrase est donc très faible, par rapport à l'autre ; son entropie est donc plus petite.
Du coup, quand on commence à écrire "six fois se...", on peut sans trop se tromper penser que les caractères suivants seront "p" et "t" : il est facile de prédire le futur d'une phrase de faible entropie. C'est en s'appuyant sur cette idée que Sinaï produit une notion d'entropie pour certains systèmes dynamiques, en s'appuyant sur les travaux de Kolmogorov (son directeur de recherche).

L'entropie de Sinaï-Kolmogorov permet donc de quantifier la complexité d'un système dynamique, et offre un moyen parfait pour mesurer le chaos. Un système à forte entropie est difficile à prévoir, tout comme il est difficile de prévoir quel sera le mot suivant d'une phrase très riche en information (forte entropie, au sens de Shannon). Si l'on s'accorde à dire que le désordre est riche en information, on peut aussi la relier à l'entropie des physiciens.

Finalement, le mathématicien Iakov Sinaï s'est inspiré de la théorie de l'information pour décrire mathématiquement des systèmes dynamiques issus de la physique. Celui qui a écrit un article intitulé "Mathematicians and Physicists = Cats and Dogs ?" a en fait passé son temps a relier les deux milieux.

---

Sources :
Site officiel du prix Abel

Images :
Yakov G Sinai photo