Deux (deux ?) minutes pour les nombres de Catalan
J'ai toujours adorté la combinatoire. Voilà pourquoi j'ai voulu lui consacrer deux (deux ?) minutes...
Deux (deux ?) minutes pour... les nombres de Catalan
Script + commentaires
1, 2, 5, 14, 42, 132,… En 1751, Leonhard Euler s’intéresse à la triangulation des polygones et obtient alors cette étrange suite de nombres.
En 1838, Eugène Catalan retrouve ces même nombres en étudiant la façon dont on peut parenthéser une expression. Il en déduira une formule relativement simple, si bien que la postérité appellera ces nombres la suite de Catalan.
Ça tombe bien, j’ai deux minutes pour en parler.
Les nombres de Catalan sont un passage obligé pour comprendre ce champ des mathématiques qu’est la combinatoire, l’art de savoir comment compter le plus efficacement possible un ensemble donné d’objets. Ils illustrent parfaitement la façon dont les mathématiciens peuvent être amenés à retourner un problème dans tous les sens pour le rendre trivial. Mais avant d’aborder le vif du sujet, ouvrons la boite à outil d’un mathématicien spécialisé dans la combinatoire.
Premier exemple tout bête. Voici un jeu de 7 familles. Il compte 7 familles. Dans chaque famille, on peut compter 6 personnages. Combien de cartes y a-t-il en tout dans ce jeu ? Si tu penses qu’il y en a 7×6, soit 42, tu as saisi toute la subtilité dont il faut faire preuve en dénombrement. Le meilleur moyen de compter les cartes n’est pas de les compter une à une, mais plutôt de considérer que l’on cherche à calculer le cardinal du produit cartésien de deux ensembles finis comptant respectivement 6 et 7 éléments… Dans des termes plus simple, on dira que l’on a fait une multiplication.
J'ai réellement créé un jeu de 7 familles autour des concepts mathématiques. malheureusement, je n'ai pas prévu que ça intéresserait qui que ce soit, alors je n'ai créé que de toutes petites cartes...
Allez, un autre exemple ! Je distribue ces 42 cartes à trois personnes de façon à ce que chacune reçoive le même nombre de carte. Elles recevront donc chacune… oui, 14 carte, il fallait procéder à une division !
Heureusement, le mathématicien a des outils un peu plus subtils pour aborder les problèmes de combinatoire, comme les factorielles, les arrangements et les combinaisons.
Nouvel exemple : je souhaite ranger mes 7 romans de la saga Harry Potter dans mon étagère. De combien de façon vais-je pouvoir les ordonner ? Je peux par exemple les ranger par ordre alphabétique, par nombre de page ou simplement par ordre chronologique. On pourrait tenter de lister tous les rangements possibles, mais cela risque d’être un peu long. Prenons plutôt le problème d’un autre point de vue. Pour le premier livre que je vais ranger, j’ai 7 choix possibles. Une fois ce premier choix effectué, il ne reste plus que 6 choix pour le deuxième livre. Il reste ensuite 5 choix pour le suivant, et ainsi de suite. On peut donc conclure qu’il existe 7×6×5×4×3×2×1 façons différentes de classer cette saga, soit 5040. Ce nombre est ce que l’on appelle la factorielle de 7. On peut être tenté de dire qu'il y a 7×7×7×7×7×7×7 rangements possibles (7 choix possibles pour chacune des positions ou 7 positions possibles pour chaque livre), mais ça serait sous-entendre que l'on dispose de plusieurs exemplaires du même livre, ou que l'on place deux livres différents au même emplacement.
De manière plus générale, on appelle factorielle d’un nombre entier N le produit décroissant de tous les nombres entiers de N jusqu’à 1, que l’on note par un point d’exclamation. La factorielle de N est donc le nombre de façon d’ordonner N objets différents.
Continuons le rangement. C’est maintenant ma collection des 24 DVD James Bond que je veux ranger. Malheureusement, mon étagère est trop petite, et je n’ai la place que d’en mettre 4. De combien de façons différentes pourrai-je alors les ranger ? Dans ce dénombrement, l’ordre est important. Plutôt que de compter une à une les possibilités, on va utiliser la même astuce que pour le problème précédent. J’ai 24 choix pour poser le premier DVD, puis 23 pour le suivant, et ainsi de suite. Puisque je ne veux ranger que 4 DVD, le nombre total s’élève à 24×23×22×21, soit au total 255 024. On parle de nombre d’arrangements.
De manière plus générale, on appelle arrangement de K parmi N le produit décroissant des K premiers entiers en partant de N et on le note ANK. L’arrangement de K parmi N désigne donc le nombre de façons de ranger K objets choisis parmi N différents. Un petit coup d’œil sur la définition des arrangements permet d’obtenir la formule ANK = N!/(N-K)!.
Un dernier outil incontournable de la combinatoire, les combinaisons. Pour parfaire mon étagère, j’aimerais y ajouter quelques figurines légo. J’en ai 25 différentes, et je veux en placer 4. Combien ai-je de façons de choisir 4 figurines parmi ces 25 ? On a envie de répondre avec les arrangements de 4 parmi 25, c’est à dire 25×24×23×22, mais ce n’est pas vraiment la réponse attendue, puisque l’ordre n’intervient pas ici. Chaque sélection de 4 figurines intervient en effet dans plusieurs arrangements différents. Mais dans combien exactement ? Eh bien, on peut le dénombrer, puisque l’on cherche ici le nombre de façons différentes de ranger 4 figurines différentes, ce qui se dénombre avec les factorielles : il y en a exactement 4×3×2×1.
Le nombre de façons de choisir les 4 figurines est donc égal au nombre d’arrangements de 4 parmi 25 divisé par la factorielle de 4, soit (25×24×23×22)/(4×3×2×1), ce qui donne tout de même 12 650. Ce nombre est appelé combinaison de 4 parmi 25.
De manière plus générale, on appelle combinaison de K parmi N, ou plus laconiquement K parmi N, le nombre d’arrangements de K parmi N divisé par la factorielle de K. La combinaison de K parmi N désigne alors le nombre de façons de choisir K objets parmi N différents. On le note parfois CNK, mais plus couramment en plaçant K sous N entre deux parenthèses. Vous connaissez peut-être ces nombre sous le nom de coefficients binomiaux, que l’on retrouve dans le triangle de Pascal, des nombres disposés en triangles où chacun est égal à la somme des deux nombres juste au-dessus. À noter enfin que la formule de K parmi N peut se réécrire sous la forme N!/((N-K)!×K!). Il me semblait important de le dire.
Ces quelques outils, mais surtout le dernier, permettent de résoudre bien des problèmes de dénombrement. Par exemple, combien existe-t-il de combinaisons différentes à l’Euromillions ? Il faut y cocher 5 numéros parmi 50, et 2 étoiles parmi 12. Puisqu’on ne tient pas compte de l’ordre, on dispose au total de 5 parmi 50 choix pour les numéros, et de 2 parmi 12 choix pour les étoiles, soit 2 118 760 combinaisons de numéros, et 66 combinaisons d’étoiles. Chaque combinaison de numéros peut être associée à n’importe quelle combinaison d’étoiles, ce qui donne donc au total 2 118 760 × 66 grilles possibles, soit au total 139 838 160.
Autre exemple de problème de combinatoire, celui des tintements de verres. Lors d’une soirée réunissant 13 amis et pas mal de boissons, deux invités annoncent l’arrivée d’un heureux évènement. Naturellement, chaque invité lèvera son verre afin de trinquer une et une seule fois avec chacun des autres invités. Combien entendra-t-on alors de tintements de verres ?
Il y a plusieurs façons de raisonner, ce qui donnera plusieurs réponses différentes mais pourtant équivalentes. On peut essayer de compter directement le nombre de tintements de verres. Déjà, l’invité A trinquera avec chacun des 12 autres invités, ce qui donne les 12 premiers tintements. L’invité B ayant déjà trinqué avec l’invité A, cela donne donc 11 tintements supplémentaires. L’invité C ajoutera 10 tintements, et ainsi de suite. Au final, le nombre de tintements s’élèvera à 12+11+10+..., soit 78.
On peut aborder le problème différemment, en considérant que chacun des 13 invités doit trinquer avec les 12 autres. Cette façon de compter ne tenant pas compte du fait que chaque tintement sera compté deux fois, il faut donc diviser le résultat par 2. Au total, le nombre s’élève donc à 13×12/2, soit 78, le compte est bon.
Une dernière façon voir le problème est de se placer du point de vue des verres. Un tintement, c’est la rencontre de deux verres. Il y a donc autant de tintements que de façons de choisir 2 verres parmi les 13. Le nombre est donc égal à 2 parmi 13, soit… 78. Un même problème trois approches différentes.
Un dernier exemple pour la route avant de parler des nombres de Catalan. Dans ce rectangle de dimension 10 sur 10, combien existe-t-il de façons de relier le point A au point B en n’empruntant que des chemins vers le haut ou vers la droite ? La réponse ne saute pas au yeux, mais il faut à nouveau faire intervenir les combinaisons. En effet, un chemin valide est une succession de 20 déplacements vers le haut ou la droite. Dans cette succession de déplacements, on comptera toujours 10 déplacements vers le haut, et tout autant vers la droite. Pour fabriquer un chemin valide, il faut donc choisir où seront ces 10 déplacements vers le haut parmi les 20 déplacements. Il y en a donc 10 parmi 20, c’est à dire 184 756 au total.
Bref, quand on est en face d’un problème de dénombrement, on peut souvent s’en sortir en utilisant de façon maline les combinaisons, surtout si l’on parvient à regarder le problème de la bonne façon.
Revenons en 1751. Durant sa très féconde correspondance avec Christian Goldbach, Leonhard Euler s’est intéressé à la question des triangulations des polygones.Oui, je me suis emmêlé les pinceaux, ce n'est pas le portrait de Goldbach dans la vidéo, mais celui de Riemann. Mea culpa !
De quoi s’agit-il exactement ? Détaillons un peu. Voici un polygone régulier à N côtés. En y traçant N-3 diagonales qui ne se croisent pas, on découpe le polygone en pièces triangulaires. On dit alors que le polygone est triangulé. Une question légitime qui se pose est le nombre de triangulations d’un polygone donné. À la main, on peut facilement vérifier que le carré n’a que 2 triangulations possibles, le pentagone en a 5 et que l’hexagone en a 14. Avec un peu de volonté, on peut vérifier que l’heptagone a 42 triangulations. Euler est parvenu à calculer à la main et sans erreurs le nombre de triangulations de tous les polygones réguliers jusqu’au décagone, et a conjecturé une formule de son cru permettant de calculer EN, le nombre de triangulations du polygone à N+2 côtés. Il n’arrive cependant pas à démontrer ce résultat.
Il en parle alors à Johann Segner, qui lui fait remarquer une façon ingénieuse de dénombrer les triangulations. Prenons l’exemple de l’undécagone, polygone à 11 côtés que Euler n’a pas essayé de traiter, et numérotons ses côtés et ses sommets de 1 à 11. Quand il sera triangulé, le côté 1 fera parti d’un triangle. Dans cet exemple, il lie le côté n°1 au sommet n°5. Si on retire ce triangle, on obtient deux sous polygones. Dans l’exemple, ils ont respectivement 5 côtés et 7 côtés. Euler a calculé qu’un pentagone possède 5 triangulations, et qu’un heptagone en possède 42. On peut donc affirmer qu’il existe 5×42, c’est à dire 210 triangulations de l’undécagone qui possèdent ce triangle liant la face n°1 au sommet n°5. En procédant de la même façon, et grâce à la connaissance du nombre de triangulations des polygones plus petits, on peut compter les triangulations de l’undécagone qui possèdent un triangle liant la face n°1 au sommet n°2, n°3, n°4 ou n’importe quel sommet jusqu’au n°10. On a ainsi compté l’ensemble des triangulations de l’undécagone, il y en a 4862.
En généralisant ce processus, on obtient la formule récursive de Segner, qui a permis à Euler de démontrer une bonne fois pour toutes sa formule donnant le nombre de triangulations d’un polygone à N côtés. En effet, une telle formule donne naissance à une équation fonctionelle plutôt facile à résoudre, mais très calculatoire. L'article de Wikipedia détaille cette preuve. La suite de nombres 1, 2, 5, 14, 42, ... devient alors la suite de Euler-Segner.
En 1838, Eugène Catalan s’intéresse à un autre problème qu’il relie tout de suite aux travaux de Euler et Segner, celui du nombre de façons de faire une multiplications à plusieurs facteurs. La multiplication à 3 facteurs 1×2×3, par exemple, peut être traitée de deux façons différentes : on peut commencer par traiter 1×2, puis multiplier le résultat par 3, ou bien commencer par 2×3, et multiplier le tout par 1. Un produit à trois termes peut donc être effectué de 2 façons différentes. Cela revient en fait au nombre de façon de parenthéser le produit 1×2×3.
Pour un produit à 4 facteurs, on peut voir qu’il y a 5 façons de le traiter, et qu’il y en a 14 pour en aborder un à 5 facteurs. Autrement dit, il y a autant de façons de faire une multiplication à N termes que de façons de trianguler un polygone à N+1 côtés.
Le lien entre les deux problèmes, Catalan le fait en remarquant que la formule de Segner s’applique dans les deux cas. La démonstration est donc calculatoire, et ne montre alors pas un lien direct entre les deux phénomènes. Il prouve cependant, toujours de manière calculatoire, une formule permettant de faire ce dénombrement. En appelant CN le nombre de façons de multiplier N+1 termes, il prouve que CN = (N parmi 2N) - ((N+1) parmi 2N), que l’on peut montrer facilement comme égal à N parmi 2N divisé par N+1. Les formules sont belles, les nombres deviennent alors les nombres de Catalan.
On a donc d’un côté des triangulations de polygones, de l’autre des parenthésage de multiplications, au milieu de tout ça des jolies formules, mais aucun liens profonds entre tout ça.
On peut pourtant en trouver, en associant à chaque triangulation un parenthésage, et inversement. Prenons par exemple un heptagone, et associons à chaque côté un facteur du produit a×b×c×d×e×f. On garde aussi un côté libre. Après avoir triangulé le polygone, on va voir qu’il est possible d’associer une expression à chacune des diagonales. Pour cela, on fait en sorte que dans chaque triangle, un côté soit égal au produit des deux autres. On commence ainsi par les diagonales qui bordent des côtés nommés de l’heptagone. Sur l’exemple, on a une diagonale qui correspond à b×c, et une autre qui correspond à d×e, puis on poursuit de proche en proche. On obtient finalement un parenthésage de l’expression a×b×c×d×e×f.
Ainsi, on montre qu’à toute triangulation de polygone à N+1 côtés correspond un unique parenthésage d’un produit de N facteurs, et réciproquement. Le problème de Euler et celui de Catalan sont donc deux facettes différentes d’un même problème.
En 1857, Arthur Cayley et Thomas Kirkman s’intéressent à un problème qui n’a a priori rien à voir, celui du décompte des arbres enracinés, structure bien connu aujourd’hui par ceux qui s’intéressent à l’informatique. Un arbre est une structure mathématique composée de différents nœuds reliés par des arêtes, mais qui ne présente aucun cycle. Sur un arbre, les nœuds situés aux extrémités sont appelés les feuilles. On dit que l’arbre est enraciné lorsque l’un des nœuds a été choisi pour en être la racine. Ils cherchent alors à dénombrer le nombre d’arbres enracinés ayant un nombre d’arêtes donnés. Par exemple, pour 2 arêtes, on compte 2 arbres ; pour 3 arêtes, on en compte 5, et pour 4, on en compte 14. Oups, j'ai dessiné deux fois le même arbre. Je me rattrappe, avec la bonne illustration :
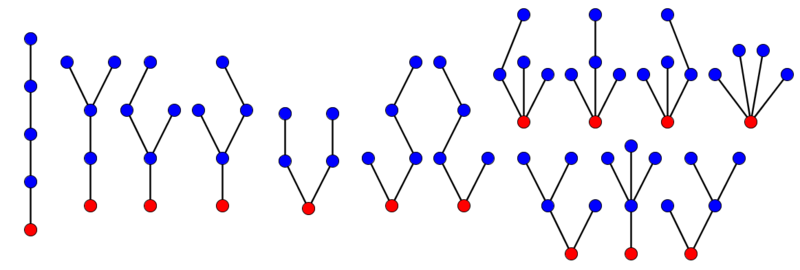
Les 14 arbres enracinés à 4 arêtes.
Ce sont bien sûr les nombres de Catalan, que nos deux mathématiciens ne reconnaissent pas du tout. Par une étude numérique, ils obtiennent cependant une formule donnant le nombre d’arbres enracinés, qu’ils considèrent remarquable. Ces nombres deviennent alors les nombres de Cayley-Kirkman.
Ils ne s’arrêtent pas aux arbres enracinés, mais étudient aussi les arbres binaires entiers, des arbres enracinés où chaque noeud interne a toujours 2 noeuds fils. Les plus biologistes d’entre vous parleront d’arbres phylogénétiques. Quand on cherche à les compter, on remarque qu’il y a 2 arbres à 3 feuilles, 5 arbres à 4 feuilles ou 14 arbres à 5 feuilles, et ainsi de suite. Encore une fois, les nombres de Catalan.
Il y a donc autant d’arbres enracinés à N arêtes que d’arbres binaires entiers à N+1 feuilles. Pourquoi ? On peut s’en convaincre graphiquement en partant d’un arbre enraciné quelconque à N arêtes. On fait alors pousser de nouvelles arêtes sur cet arbre de façon à ce que chaque arête initiale deviennent une arête gauche, ce qui donne un arbre binaire entier à N+1 feuilles. Inversement, si l’on part d’un arbre binaire entier quelconque, la rétraction des arêtes droites donne des arbres enracinés. Bref, on peut associer à chaque arbre enraciné un unique arbre binaire, et inversement, il y en a donc autant.
Mais ce n’est pas tout. Si je prend un arbre binaire et que je place sur chaque feuille une lettre, j’obtiens une représentation parfaite de mon problème de parenthésage de produit. Il y a donc autant d’arbres binaires à N+1 feuilles que de parenthésages d’un produit à N+1 facteurs, et donc tout autant que de triangulation de polygone à N+2 côtés . Tout est donc lié !
Mais cela n’explique pas encore la formule de Catalan, qui prétend qu’il y en a très exactement (N parmi 2N) - ((N+1) parmi 2N). Pour le comprendre, il faut interpréter les nombres de Catalan d’une nouvelle façon, et se tourner vers les mots de Dyck.
Un mot de Dyck est un mot composé de deux lettres données, disons A et B, qui compte autant de A et de B, et tel que le nombre de A est toujours supérieur ou égal au nombre de B lorsqu’on lui retire une ou plusieurs de ses lettres finales.
Le mot AABBBAAB, de longueur 8, n’est pas un mot de Dyck, puisque lorsque l’on retire les trois dernières lettres, on compte plus de B que de A. Le mot AABAABBB est quant à lui tout à fait valide.
Une façon plus visuelle de se représenter un mot de Dyck est d’utiliser, non pas les lettres A et B, mais des parenthèses ouvrantes et fermantes. Un mot de Dyck est alors une succession valide de parenthèses, où chaque parenthèse ouverte est bien fermée. Dénombrons les mots de Dyck. Avec deux paires de parenthèses, on obtient 2 expressions, avec trois paires, on en a 5, avec quatre paires, on en trouve 14, et ainsi de suite. Ce sont bien sûr les nombres de Catalan. Pour le prouver, on peut montrer qu’il existe autant de façons de disposer N paires de parenthèses que d’arbres enracinés à N arêtes. Pour voir cela, prenons un arbre enraciné quelconque, et marquons le trajet qui en fait le tour. Lorsque l’on passe à gauche d’une arête, on le note par une parenthèse ouvrante, et sinon, par une parenthèse fermante. On peut donc associer à n’importe quel arbre enraciné à N arêtes une expression valide à N paires de parenthèses, et inversement.
On peut aussi interpréter plus géométriquement les mots de Dyck en regardant ce que l’on appelle les escaliers de Dyck. On se place dans une grille de dimension N×N, et, pour un mot de Dyck donné, on effectue le chemin sur la grille où A correspond à se déplacer d’une unité vers le haut, et B d’une unité vers la droite. On obtient un escalier de Dyck, c’est à dire un chemin reliant les sommets opposé du carré qui ne passe jamais en-dessous de la diagonale. Il y a bien sûr autant de mots de Dyck de longueur 2N que de d’escaliers de Dyck de longueur 2N.
Je n'ai pas parlé des "chemins" (ou "montagnes") de Dyck, un chemin de longueur 2N liant les points (0,0) à (0,2N) ne passant sous l'axe des abscisse, et formé de segments "montants" (une unité vers la droite puis vers le haut) ou "descendants" (une unité vers la droite puis le bas). Il s'agit en fait des escaliers de Dyck après une rotation à 45°.
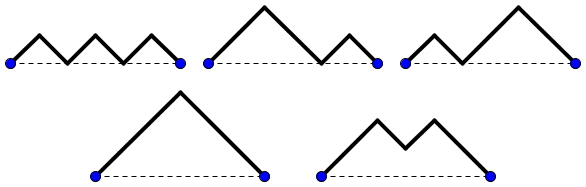
Les 5 montagnes de Dyck de longueur 2×3
L’intérêt de cette représentation des nombres de Catalan, c’est qu’elle se laisse dénombrer. Dans cette grille de dimension N×N, combien existe-t-il de chemins qui relient le point A au point B, un chemin n'étant composé que de déplacements vers le haut ou vers la droite ? Un tel chemin est composé de 2N déplacements dont N déplacement vers le haut, il y en a donc N parmi 2N au total.
Pour obtenir un escalier de Dyck, il faut rajouter l’hypothèse que le chemin ne passe jamais en dessous de la diagonale (AB). De tous les chemins reliant A et B, combien coupent cette diagonale ? Un chemin invalide, donc, qui coupe la grande diagonale [AB], touche en au moins un point, disons C, la diagonale [αβ] juste en dessous. L’astuce est de considérer un nouveau chemin, obtenu à partir du précédent. On garde la partie liant A à C, et on prend le symétrique de la partie liant C à B par rapport à la sous-diagonale [αβ]. Ce nouveau chemin relie alors A au point B’, symétrique de B par rapport à [αβ]. On peut alors voir qu’il y a autant de mauvais chemin liant A à B que de chemins liant A à B’.
Ces derniers peuvent être dénombrés facilement, puisqu’i il s’agit d’une succession de 2N déplacements comptant N+1 déplacements vers la droite. Il y a donc N+1 parmi 2N chemins liant A à B’, soit tout autant que de mauvais chemins liant A à B.
Puisque le nombre de chemin de Dyck est égal au nombre de chemins liants A à B moins le nombre de mauvais chemins liant A à B, on peut donc à présent affirmer que le nombre d’escaliers de Dyck, c’est à dire le N-ième nombre de Euler-Segner-Catalan-Caylay-Kirkman est égal à (N parmi 2N) -(N+1 parmi 2N).
Résumons la situation. Le N-ième nombre de Catalan est le nombre de triangulations d’un polygone à N +2 côtés, qui est égal au nombre de façons de parenthéser un produit de N +1 facteurs, qui est égal au nombre d’arbres binaires entiers à N+1 feuilles, qui est égal au nombre d’arbres enracinés à N arêtes, qui est égal au nombre de façons de disposer N paires de parenthèses, qui est égal au nombre de mots de Dyck de longueur 2N, qui est égal au nombre d’escaliers de Dyck de longueur 2N, qui est finalement égal à (N parmi 2N) -(N+1 parmi 2N). Je crois que c’est pour cela que j’adore la combinatoire.
C'est dans ce contexte que la citation de Henri Poincaré prend tout son sens : « la mathématique est l’art de donner le même nom à des choses différentes.».
Mini FAQ :
- Y a t il une chose que Euler n'a pas étudiée ?
Il est vrai que Euler intervient dans une vidéo sur deux (et si je n'en parle pas dans les autres, c'est juste que j'ai passé sous silence ses contributions au domaine en question). La liste des choses nommées d'après Euler de Wikipédia est absurdément grande.
- Bijection ou isomorphisme ?
L'objet de cette vidéo était bien sûr de fabriquer des bijections (fabriquer des couples liant les élements d'un premier ensemble à celui d'un deuxième de façon à ce que chaque élément du premier ensemble ne soit lié qu'à un unique élément du deuxième, et réciproquement) de façon à prouver que les ensembles possèdent le même nombre déléments. Un isomorphisme, c'est un peu plus que ça : il s'agit d'une bijection qui transporte une structure d'un contexte vers un autre. Dans tous les exemples présentés dans la vidéo, il n'y est pas question de structure - il n'est pas expliqué par exemple comment associer deux arbres pour en former un troisième, ou comment associer deux triangulations pour en former une troisième. Il est possible de le faire, et ce n'est qu'après ce travail là que l'on pourra dire que les bijections de la vidéo sont des isomorphismes !
Sources :
History of Catalan number, Igor Pak - Un excellent historique des différentes approches des nombres de catalan
Note sur une équation aux différences finies, Eugène Catalan - l'article original de Catalan
On the Analytical Forms called Trees, Arthur Cayley - l'article original de Cayley
Catalan addendum - Richard P. Stanley - une liste démesurément grande de tous les problème de combinatoire dont la réponse est les nombres de Catalan
Le Roi des Catalans, Blog de maths - Un peu plus de détails sur cette histoire de symétrie et d'escaliers de Dyck
Nombre de Catalan, Wikipedia







/http%3A%2F%2Fstorage.canalblog.com%2F06%2F96%2F210892%2F102825337_o.jpeg)
/http%3A%2F%2Fstorage.canalblog.com%2F98%2F97%2F210892%2F92096273_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F39%2F48%2F210892%2F82134058_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F26%2F88%2F210892%2F71442999_o.png)