Deux (deux ?) minutes pour... classer les pavages !
Les mathématiciens aiment classer des trucs, et avec les pavages, ils ont été servis !
Script
En mai 2017, le mathématicien français Michaël Rao (et non Mickaël, mea culpa) publie “Recherche exhaustive des pentagones convexes qui pavent le plan”. Il signe alors la fin de la classification des pavages périodiques convexes du plan, question ouverte depuis tout de même presque un siècle. C’est l’occasion de traiter de la classification des pavages, et ça tombe bien, j’ai deux minutes pour en parler.
Voici un motif quelconque. Avec plusieurs copies de ce motif, il m’est possible de fabriquer un splendide papier peint. En prenant d’autres motifs, j’obtiens d’autres papiers peints. Dans tous les cas, chaque motif peut se déduire du premier par un simple déplacement, une translation. Seulement, voilà, tous ces papiers peints sont un peu les mêmes, générés à partir d’un même motif et de translations. Est-il possible de faire des choses un peu plus inattendues ?
Eh bien, bien sûr que oui, sinon je ne poserais pas la question. Si je m’autorise à tourner les pièces, je peux obtenir à partir de mon motif de base un papier peint radicalement différent ! Celui-ci par exemple peut être généré à partir de rotations et de translations. Ce n’est donc pas simplement le motif qui produit le papier peint, mais plutôt la façon dont on peut le générer à partir de ce motif. Et s’il existe déjà deux papiers peints différents, c’est qu’il y en a davantage. Combien ? Excellente question.
Précisons un peu les termes. Nous allons parler de papier peints périodiques. Ce que je vais appeller «papier peint», c’est la répétition d’un même motif à l’infini et de façon discrète dans toutes les directions du plan. On dit qu’un papier peint est périodique quand il existe au moins deux translations de directions différentes qui transforment la globalité du papier peint en lui même. Quand ces deux translations n’existent pas, on parle de non périodicité, d’apériodicité ou de quasipériodicité suivant le contexte. Les différences sont subtiles, le sujet est intéressant, mais on en parlera probablement dans une autre vidéo, Concentrons-nous aujourd’hui plutôt sur les pavages périodiques.
On vient de le dire, on trouve toujours dans un papier peint des translations, mais on a vu que l’on peut parfois y trouver aussi des rotations. Ce n’est pas tout. On peut également retrouver d’autres transformations, comme les symétries centrales, puisque ce sont des cas particulier de rotations. Il y a aussi les symétries axiales, et enfin la symétrie glissée, c’est à dire une symétrie axiale suivie d’une translation parallèle à l’axe. Et, c’est à peu près tout. Toutes ces transformations que l’on peut retrouver dans un papier peint sont les isométries du plan, les transformations qui conservent les tailles des objets qu’elles transforment. On exclut donc les transformation qui déforment, comme les homothéties ou les inversions.
Quand on regarde un papier peint, une bonne question à se poser est celle de son groupe, c’est à dire, quelles sont les isométries que l’on y retrouve.
Prenons par exemple ce superbe papier peint fleuri vintage. Quelles isométries peut-on y retrouver ? Déjà, il y a des translations. Au moins deux, et de directions différentes, c’est bien un papier peint périodique. Ensuite, on peut voir que les bouquets se regroupent toujours par 4. Cela marque la présence de ce que l’on appelle des symétries d’ordre 4, c’est à dire, des rotations d’un quart de tour centrées sur le milieu de ces bouquets de bouquets, que ce soit les grands ou les petits. On peut enfin déceler ici et là des symétries centrales
On peut donc dire que le groupe de ce papier peint est composé de translations, de 2 familles de rotations d’un quart de tour et de 2 familles de symétries centrales.
Un second exemple, avec ce papier peint sixties. Comme toujours, des translations sont présentes, selon plusieurs directions différentes. Aucune rotation ni symétrie centrale n’est à signaler, on peut cependant voir des symétries axiales, dont l’axe est vertical. Plus difficile à repérer, on peut retrouver dans ce papier peint des symétries glissées, dont l’axe n’est pas le même que celui des symétries axiales.
On peut donc dire que le groupe de ce papier peint est composé de translations, d’une famille de symétries axiales et d’une famille de symétries glissées.
On a donc déjà décrit 4 groupes de papiers peint différent, chacune portant son petit nom. On a vu le groupe p1, composé uniquement de translations, le groupe p3, composé de translations et de rotation d’un tiers de tour, le groupe p4 composé entre autres de rotations d’un quart de tour, et le groupe cm, sans rotations, mais possédant des symétries axiales et des symétries glissées.
Mais combien existe-t-il de papiers peints différents, alors ? Eh bien, il faut faire un truc que les mathématiciens aiment faire : il faut établir la classification des groupes de papiers peints. Ce travail n’est pas fondamentalement difficile, mais est tout de même loin d’être trivial. Pour comprendre l’idée, on va établir ensemble la classification des groupes, non pas de papiers peints périodique, mais de son équivalent à une seule dimension : les frises périodique.
Alors qu’un papier peint périodique est la répétition discrète de motifs du plan stable selon deux translations, une frise périodique est la répétition discrète de motifs stable selon une seule direction. Pour plus de simplicité, on supposera ces frises horizontales. La classification des frises est plus simple que celle des papiers peints, puisque seules 5 isométries préservent les frises. Il y a, par définition, les translations. On peut également trouver des symétries centrales, des symétries d’axes verticaux, des symétries d’axes horizontaux, ou les mêmes, mais avec glissement. On retrouve toujours des translations dans les frises et, si une symétrie d’axe horizontale est présente, on aura forcément des symétries glissées, la réciproque n’étant pas vraie. Selon les isométries présente, on peut donc dénombrer a priori 12 types de frises possibles. On peut alors chercher des exemples pour chacun de ces 12 types. On a donc des frises qui présentent uniquement des translations ou, en plus des translations, uniquement des symétries d’axes verticaux, uniquement une symétrie d’axe horizontal, uniquement des symétries centrales ou uniquement des symétries glissées. On peut aussi trouver une frise qui présente toutes les isométries, ou bien toutes sauf la symétrie d’axe horizontal. Et pour les autres cases du tableau ? Essayons par exemple de construire une frise qui présente une symétries d’axe horizontal et d’autres d’axes verticaux, mais pas de symétrie centrale. On part d’un motif, et on lui applique une symétrie d’axe horizontal, puis d’axe vertical. En procédant ainsi, on retrouvera forcément dans la frise une symétrie centrale. Toutes les cases du tableau ne sont donc pas possible. En inspectant chacun des 12 cas, on peut alors conclure qu’il n’existe que 7 groupes de frises différents. Je vous invite à visionner la vidéo de Micmaths pour plus de détails.
Pour les papiers peints, le principe est le même. On commence par lister les isométries qu’il est possible d’y retrouver, et on cherche lesquelles sont possibles, et lesquelles sont impossibles. La démonstration est particulièrement laborieuse, donc je vous livre la conclusion : il en existe précisément 17 et, pour le plaisir de galérer au montage de cette vidéo, voici la liste exhaustive des 17 groupes de papiers peints :
P1, composé de translations seules
Pm, composé de translations et de symétries axiales d’axes tous parallèles
Pg, où l’on remplace les symétries axiales par des symétries glissées
Cm, composé de translations, de symétries axiales et de symétries glissées, d’axes tous parallèles
Pmm, composé de translations, et de symétries axiales selon deux directions perpendiculaires
Pgg, composé de translations, et de symétries glissées selon deux directions perpendiculaires
Pmg, qui est un compromis entre pmm et pgg : une direction de symétrie axiales, une autre de symétrie glissée
Cmm, un autre type de compromis : deux directions de symétries axiales, et des symétries glissées en parallèle
P2, composé de symétries centrales seules, en plus des translations
P4, qui y ajoute les rotations d’un quart de tour
P4g, qui ajoute des axes de symétries axiales selon deux directions perpendiculaires
P4m, qui rajoute des symétries axiales selon deux autres directions
P3, composé de translations et de symétries d’un tiers de tour
P6, qui y rajoute des symétries d’un sixième de tour
P6m, qui y rajoute un nombre impressionnant de symétries axiales
P3m1, composé de translations, de symétries axiales selon 3 directions et de symétries d’un tiers de tour dont les centres sont tous aux points d’intersection des axes de symétries
En enfin, p31m, qui a les mêmes éléments que le précédent, mais dont les centres de symétrie ne sont pas tous aux points d’intersection des axes de symétries
Y en a t-il d’autres ? Non ? Vais-je vous le prouver ? Non plus, puisque plusieurs mathématiciens l’ont fait avant moi, je leur fais confiance.
Bizarrement, l’histoire a pris son temps avant de prouver qu’il n’existe que 17 groupes de papiers peints. Le premier à avoir tenté de les classifier semble être Camille Jordan en 1868, qui n’en a déterminé que 16 sur les 17. La classification complète est attribuée au mathématicien russe Evgraf Fedorov, en 1891, qui a prouvé une bonne fois pour toutes qu’il n’y en a pas plus de 17. Il peut sembler assez étonnant de voir que l’étude des symétries des papiers peints est si récente, quand on sait que la quasi totalité des types de papiers peints et de frises se retrouvent dans les arts de l’Islam, notamment sur les murs de l’Alhambra à Grenade, groupe de palais construits à partir du XIIIe siècle. En fait, l’étude minutieuse des symétries du plan ne pouvait exister sans le concept de groupe, concept incontournable en mathématiques mais qui n’a été introduit qu’au cours du XIXe siècle. Il semble également que la classification des symétries du plan intéressait moins que celle des symétries de l’espace, indispensable à la cristallographie pour les chimistes. En réalité, quand Fedorov décrit les 17 groupes de papiers peints, c’est seulement en préambule de la description complète des 230 groupes d’espaces, l’équivalent 3D des groupes de papier peint.
Mais quand les mathématiciens se décident à classer des choses, ils ne s’arrêtent pas si simplement. On a classé les papiers peints, mais pas encore les motifs que l’on peut y trouver. On va alors arrêter de parler de papiers peints, mais plutôt parler de pavages.
Un pavage, c’est donc un papier peint où l’on retrouve un ou plusieurs motifs, les tuiles, qui recouvrent la totalité du plan, sans trous ni chevauchement. Il en existe de nombreux types, et mettre de l’ordre dans tout ça demande un peu de patience.
Par exemple, on peut chercher les pavages périodiques où les tuiles sont des triangles équilatéraux, des carrés, des pentagones réguliers ou n’importe quel autre polygone régulier. On parle de pavages uniformes, et rien que ceux-là peuvent très vite devenir pénibles à trier.
Déjà, on peut chercher les pavages dont toutes les tuiles sont les mêmes polygones réguliers. On a ainsi le pavage triangulaire, constitué de triangles équilatéraux ; le pavage carré constitué, ben, de carrés et le pavage hexagonal, constitué d’hexagones réguliers. Est-ce que c’est tout ? Eh bien, oui, et non. Non, parce que aucun autre polygone régulier ne peut paver le plan. Si on prend par exemple un pentagone régulier, on sait que ses angles mesurent tous 108°. Ainsi, trois pentagones collés à un même sommet ne laissent disponible qu’un angle de 36°, ce qui ne laisse pas la place à un autre pentagone. Bref, pas de pavages par des pentagones réguliers uniquement, non plus avec des heptagones réguliers, ou des polygones à davantage de côtés.
Seulement, si on prend des tuiles carrées, il n’y a pas que le pavage en quadrillage qu’il est possible de construire. En décalant les rangées, il est possible d’en fabriquer d’autres, mais ceux-ci sont moins satisfaisant. Le pavage que l’on obtient n’est pas un pavage côté contre côté, où chaque côté de chaque polygone n’est en contact qu’avec un seul autre polygone. Il existe une infinité de pavages réguliers différents par des carrés qui ne soient pas côtés contre côtés, il est donc raisonnable de les exclure de notre classification.
Un autre point que l’on pourrait prendre en compte est celui de la coloration des polygones. En attribuant une couleur à chaque tuile, les pavages obtenus sont les mêmes, mais les papier peint obtenu ne seront pas nécéssairement les mêmes. Par exemple, en coloriant le quadrillage carré comme un échiquier, le papier peint possèdera des symétries d’un quart de tour, ce qui n’est plus le cas si l’on colorie une bande sur 2. Les coloriages intéressants sont les coloriages uniformes, lorsque ce sont les mêmes couleurs dans le même ordre que l’on retrouve autour de chaque sommet du pavage. On peut alors les dénombrer : il existe ainsi 9 coloriages uniformes différents du pavage carré, 9 pour le pavage triangulaire et 3 pour le pavage hexagonal.
Lorsqu’un pavage côté contre côté présente un unique type de polygone régulier, on parle de pavage régulier, ou de pavage platoniciens. Il n’en existe donc que trois : le pavage carré, le pavage triangulaire et le pavage hexagonal.
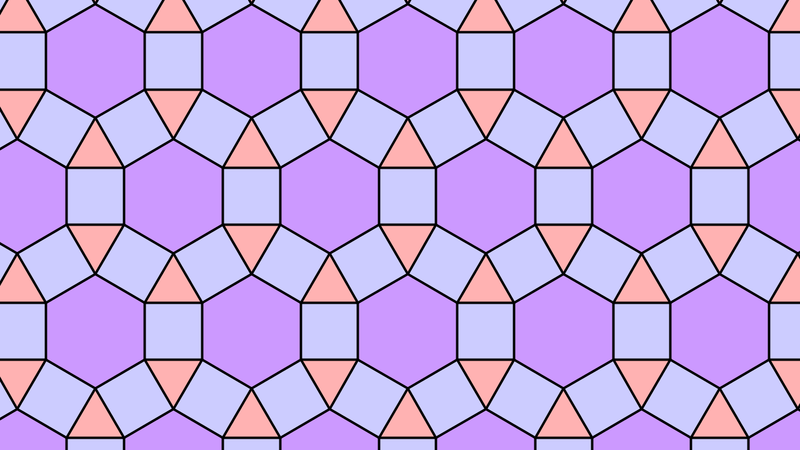
Et si, au lieu de n’utiliser qu’un seul type de polygone, on en utilise plusieurs ? Là, ça peut donner des pavages périodique qui peuvent être affreux, comme par exemple celui-ci, composé de bandes de carrés et de bien trop de bandes de triangles. Pour ne pas avoir une infinité de cas possibles, on va se restreindre aux pavages uniformes, où, en chaque sommet du pavage se réunissent les mêmes polygones dans le même ordre. On parle parfois de pavages archimédiens. C’est par exemple le cas du pavage carré adouci, où en chaque sommet se retrouvent deux carrés et trois triangles équilatéraux. Avec un peu de calculs, on peut retrouver la liste complète des pavages uniformes. En effet, on peut prouver que si des polygones réguliers forment un pavage uniforme, alors la somme de l’inverse de leur nombre de côtés vaut toujours ½. Cette équation traduit le fait que tous les sommets du pavage sont équivalent, et on peut calculer qu’elle possède 21 solutions, soit tout autant de pavages potentiels. En fait, toutes les solutions de l’équation ne donnent pas des pavages, c’est par exemple le cas de la solution 5, 5 et 10. Finalement, c’est seulement 11 pavages uniformes qu’il existe au total et ça me fait plaisir de vous les lister. Il y a les trois pavages régulier, le carré adouci, l’hexagonal adouci, le carré tronqué, l’hexagonal tronqué, le tri hexagonal, le petit rhombi tri hexagonal, le grand rhombi tri hexagonal et enfin le triangulaire allongé. On peut remercier Johannes Kepler d’avoir le premier exploré le sujet.
Ça, c’était pour les pavages où tous les sommets sont équivalents. Et lorsque ce n’est plus le cas, on peut quand même lister des choses. Par exemple, si il n’existe pas qu’un seul type de sommet, mais plusieurs types différents, on parlera de pavages k-uniformes, où k est le nombre de sommets différents. Prenons par exemple ce pavage, sobrement baptisé pavage 3-4-6-12, qui possède deux types de sommets différents. Il y a ceux réunissant deux carrés, un triangle et un hexagone, et ceux réunissant un carré, un hexagone et un dodécagone. Puisque ce pavage possède deux types de sommets, on dit qu’il est 2-uniforme. On sait aujourd’hui qu’il existe précisément 20 pavages 2-uniformes, 61 pavages 3-uniformes, et ainsi de suite. Je vous fais une fleur : je ne vais pas vous les lister. On ne connait cependant pas aujourd’hui le nombre de pavages 7-uniformes ou 8-uniformes. Avis aux amateurs…
On a donc classé les types de symétries que l’on retrouve dans les papiers peints périodiques. On a classé les pavages périodiques que l’on peut fabriquer avec les polygones réguliers. Il y a encore quelque chose que l’on a pas classé, ce sont les polygones qui peuvent paver le plan de façon périodique. On sait que seuls trois polygones réguliers peuvent paver le plan, mais qu’en est-il des autres, ceux qui ne sont pas réguliers ?
Par exemple, peut-on toujours paver le plan avec des triangles quelconques ? Eh bien, oui, et il y a une recette qui marche à chaque fois. En accolant deux triangles identiques, on peut toujours former un parallélogramme, qui peut paver le plan. Problème résolu, tout triangle pave le plan.
Et pour les quadrilatères ? Là aussi, on peut résoudre facilement le problème, puisque n’importe lequel peut paver le plan. Il suffit qu’en chaque sommet du pavage se retrouvent chacun des 4 sommets du quadrilatère.
Pour les polygones ayant davantage de côtés, c’est forcément plus compliqué. On a par exemple vu que les pentagones réguliers ne peuvent pas paver le plan. Il y a donc obligatoirement des critères à respecter pour qu’un polygone à 5 côtés ou plus puisse paver le plan.
Pour ne pas nous compliquer trop la tâche pour le moment, on va se concentrer sur les polygones convexes, ceux qui ne possèdent pas de creux. On connait beaucoup de polygones non convexes qui permettent de paver le plan, et la classification est aujourd’hui en 2017 loin d’être achevée. En se limitant aux polygones convexes, on s’enlève une bonne épine du pied, puisqu’on peut prouver qu’un polygone convexe ne peut pas paver le plan si il possède 7 côtés ou plus. En effet, la somme des angles d’un heptagone vaut 900°, soit une moyenne de 128° par angle. Si il existe un pavage d’heptagones convexes que l’on peut supposer côté contre côté, le nombre moyen d’heptagone par sommet sera donné par 360/128, soit 2.8. Puisqu’il faut au moins 3 heptagones par sommet, un tel pavage est impossible. Il ne reste donc que le cas des pentagones et des hexagones à traiter.
Commençons par les hexagones : il y a un critère pas trop compliqué qui permet de savoir si un hexagone convexe peut paver le plan. Un hexagone convexe peut paver de façon périodique le plan si et seulement si
- il possède deux côtés opposés parallèles de même longueur OU
- il possède deux côtés opposés de même longueur, dont l’un est entouré de côté de même longueur OU
- il possède trois paires distinctes de côtés égaux formant des angles de 120°
Autrement dit, un hexagone convexe pave le plan si et seulement si il fait partie d’au moins l’une de ces trois classes. Rien n’empêche qu’un hexagone fasse partie de plusieurs classes différentes, comme c’est le cas de l’hexagone régulier qui vérifie tous les critères. De plus, chaque classe d’hexagone permet de construire un pavage qui lui est propre, mais un même pavé peut parfaitement donner des pavages radicalement différents. Ce que dit surtout ce théorème, c’est que si un hexagone ne vérifie aucun de ces critère, alors c’est sûr qu’il ne pavera pas le plan.
Et pour les pentagones ? A l’instar des hexagones, il y a différentes classes de pentagones qui pavent le plan, et il faut et suffit de rentrer dans l’une de ces classes pour générer un pavage régulier du plan. Il existe 15 classes de pentagones qui pavent le plan, et l’histoire de leur découverte mérite d’être racontée.
Tout commence en 1918, dans la thèse de Karl Reinhardt. Il écrit qu’un polygone peut paver périodiquement le plan si et seulement si il fait partie de l’une des classes de pavé suivante :
Classe 1 : le pentagone possède deux côtés parallèles
Classe 2 : le pentagone possède deux côtés opposés égaux, ces côtés formant avec deux côtés non adjacents des angles supplémentaires
Classe 3 : trois copies du pentagone peuvent former un hexagone
Classe 4 : le pentagone possède deux paires distinctes de côtés égaux forment des angles droits
Et enfin, classe 5 : le pentagone possède deux paires distinctes de côtés égaux, l’une formant un angle de 120°, l’autre de 60°.
Reinhardt conclut que ce sont les seules classes de tuiles pentagonales qui existent, qu’i est inutile d’en chercher plus. L’histoire lui donnera tort, puisqu’il est quand même passé à côté de 10 autres. Ce qu’il s’est passé, c’est qu’il n’a en fait trouvé que les tuiles pouvant donner des pavages isoédriques. On dit qu’un pavage est isoédrique lorsque toutes les tuiles y sont équivalentes. Plus précisément, pour deux tuiles quelconques du pavage, il faut qu’il existe toujours une symétrie du pavage qui transforme l’une des tuiles en l’autre. Prenons ce pavage, par exemple. Les tuiles opposées par leur sommet droit se déduisent l’une de l’autre par une symétrie centrale, laquelle est bien une symétrie du pavage, pas de problème. Par contre, deux tuiles côte à côte se déduisent l’une de l’autre par une rotation d’un quart de tour, transformation qui n’est pas une symétrie du pavage. Au regard donc de ces symétries, toutes les tuiles ne sont pas équivalentes, ce pavage n’est pas isoédrique. Ce que Reinhardt a prouvé, c’est qu’il n’existe que 5 tuiles donnant des pavages isoédriques, mais n’a pas pensé qu’il pouvait en exister d’autres.
La question des pavages pentagonaux restera mise de côté pendant 50 ans, jusqu’à ce que Richard Kershner découvre 3 nouvelles classes de pavés pentagonaux. Cette fois, c’est sûr, pour Kershner, il n’y en a pas d’autres. Il n’a bien sûr pas la place dans les pages de l’American Mathematical Monthly pour prouver ses dires…
Quelques années plus tard, Martin Gardner écrit dans le Scientific American un article relatant les découvertes de Kershner, et c’est à ce moment que le problème des pavages pentagonaux quitte le milieu des mathématiciens professionnels un peu trop sûr d’eux pour celui des amateurs. D’abord avec Richard James, informaticien, qui découvre une nouvelle tuile, et s’empresse de l’envoyer à Gardner. Après qu’il a écrit un nouvel article pour relater la découverte d’un nouveau pavage, ce ne sont pas moins de 4 pavages supplémentaires qui seront découvert par Marjorie Rice, une femme au foyer sans haute formation mathématiques tombée par hasard sur le magazine de son fils. Hommage à Marjorie Rice, décédée à peine deux mois après la découverte de Michael Rao. Vous pouvez retrouver l'étendue de son travail sur son site internet. Contrairement aux professionnels, ces amateurs ne cherchent pas à avancer que la liste est terminée.
Ce sont donc à présent 13 pavages pentagonaux que l’on connaît. En 1985, une 14e classe est découverte, par le mathématicien Rolf Stein. Bien sûr, il affirme que la liste est complète, et bien sûr, il se plante dans sa démonstration.
La 15e et dernière classe sera découverte en 2015 par les mathématiciens Casey Mann, Jennifer McLoud et leur étudiant. En faisant preuve pour une fois d’un peu de sagesse, ils n’affirment pas que la liste est exhaustive. Ils auraient pu, puisque, effectivement, la liste était bien complète, ce qui a été prouvé en mai 2017 par Michael Rao. Son objectif était de découvrir de nouveaux pavages en testant méthodiquement tous les pavés possibles. Il n’en a pas trouvé de nouveaux, la conclusion est donc qu’il n’en existe pas d’autres. La démonstration utilise donc en grande partie l’informatique, et on ne va pas rouvrir le débat sur la validité d’une telle preuve.
La classification des tuiles convexes est donc aujourd’hui achevée : les polygones qui peuvent paver le plan sont donc les triangles, les quadrilatères, 3 classes d’hexagones, 15 classes de pentagones et c’est tout. Je n’en ai pas parlé, mais on a aussi la liste des pavages isoédriques par des polygones convexes, les pavages où toutes les tuiles sont dans des positions équivalentes. Il en existe précisément 107.
Peut-on alors considérer que la classification des pavages périodiques est bien terminée ? La question des tuiles pentagonales était la véritable dernière question encore ouverte donc, sur ce point, c’est oui. Il faut dire que l’informatique a bien aidé les chercheurs et les amateurs à mettre de l’ordre dans tout ça. Mais il reste malgré tout bien d’autres questions. Il y a déjà la classification des pavages k-uniformes, que l’on connait en partie, mais qui très vite ne présente aucun intérêt. Il y a aussi la classification des pavages périodiques convexes mais non isoédriques en fonction de leur complexité, un chantier loin d’être évident à aborder. Du côté des tuiles non convexes, c’est surtout les polyominos que l’on a étudié, c’est à dire les tuiles composées de carrés accolés. Là aussi, des classifications sont faites en fonction de la complexité des polyominos ou des pavages, je ne vais pas m’étendre davantage sur le sujet. Un autre problème très actuel à propos des tuiles non convexe est de savoir s’il existe des critères permettant de dire si une tuile donnée peut oui on non paver le plan. Il y a aussi la question des pavages qui ne sont pas périodiques. Ces structures sont très récentes, et avant de chercher à mettre de l’ordre dans tout ça, il faut commencer par prendre la pleine mesure de ce que le sujet recouvre et la tâche n’est pas simple. Cela ferait un très bon sujet pour une autre vidéo, non ?
FAQ
- Peut-on paver le plan avec des tuiles non pas polygonale, mais formées par des courbes de Jordan quelconques ?
Deux possibilités. Si elles sont convexes, alors elles ne paveront jamais le plan (trois courbes ne peuvent pas se réunir en un seul point sans former d'angles). Si elles ne sont pas convexes, alors il n'y a pas vraiment de moyens aujourd'hui pour faire des classifications intéressantes.
- Peuton paver le plan hyperbolique ?
Là, il y a un théorème intéressant : tous les polygones réguliers peuvent paver le plan hyperbolique ! Je vous laisse faire vos recherches sur ce sujet...
Sources :
Wallpaper symetry, applet en ligne pour test les 17 papiers peints
The tiling viewer, J. Scherphuis, applet en ligne pour visualiser tous les pavages convexes connus
Spacegroups, applet à télécharger pour visualiser les 230 groupes d'espace
Album-photo des pavages que j'ai dessiné pour les besoins de cette vidéo
Wallpaper groups, J. Zavadlav
Pavages périodiques, V. Pilaud
History of crystallographic groups and related topics, D. E. Joyce
Wallpaper group, sur wikipedia
What symmetry groups are present in the Alhambra, B. Grünbaum
The Alhambra and the Alcazar, Math & the Art of Escher
Tilings by regular polygons, D Chavey
n-Uniform Tilings, B. Galebach
On paving the plane, R. Kershner
Exhaustive search of convex p entagons which tile the plane, Michael Rao
Pentagon Tiling Proof Solves Century-Old Math Problem, Quanta magazine



/http%3A%2F%2Fstorage.canalblog.com%2F86%2F18%2F210892%2F132380602_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F43%2F78%2F210892%2F106322231_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F67%2F62%2F210892%2F68963066_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F02%2F16%2F210892%2F36491502_o.jpg)