Puisque le Petit Prince l'a dit

C'est bien joli de parler de maths, mais pourquoi ne pas parler un peu de littérature ?!...
Je me sens d'humeur à parler d'Antoine de Saint Exupéry, du Petit Prince... Pourquoi ne pas faire une petite analyse de la portée philosophique de l'œuvre ? En effet, ça... Nan, parlons plutôt de maths, je suis là pour ça !

On prête à Antoine de Saint Exupéry un dialogue entre lui et le Petit Prince, conversation durant laquelle le Petit Prince affirme sans sourciller son théorème (Le théorème du Petit Prince) : "Si un triangle a trois angles droits, alors il est équilatéral".

Ce à quoi vous aimeriez bien lui répondre  : "Et la marmotte, elle met le chocolat dans le papier d'alu. C'est pas possible d'avoir trois angle droits dans un triangle ! Rho le nul !".
Ce à quoi le Petit Prince vous répondrait, sûrement avec dédain, que vous avez tort, et commencerait à vous faire la morale. Et pour vous enfoncer encore plus, il vous dessinerait ce fameux triangle :

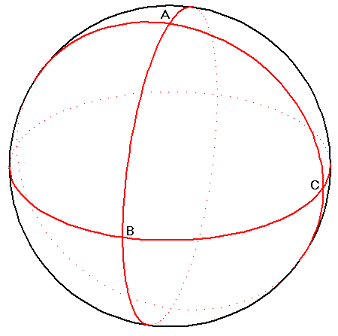
Le triangle ABC est bien un triangle équilatéral qui possède trois angle droits...

Et toutes ces histoires comme quoi la somme des mesures des angles d'un triangle est toujours égale à 180° ?... Eh oui, on vous a toujours menti, mais rassurez-vous, c'était pour votre bien...

-------

Il est donc l'heure de découvrir la vérité : tout ce que l'on apprend en géométrie depuis la maternelle, ce n'est qu'une vision euclidienne du domaine... Petit cours approximatif de l'histoire des mathématiques.

Avant Euclide, on faisait de l'arithmétique et de la géométrie, sans trop se poser de questions philosophiques comme "qu'est ce qu'un point ?" ou "qu'est ce qu'une droite". Vers 300 avant JC, Euclide en avait marre de tout ça, mit les pieds dans le plat et donna tout un tas de définitions sur ces concepts (Ndlr : totalement indigestes).
A partir de toutes ces définitions, il donna 5 postulats (des propriétés que l'on décide vraies et sur lesquelles on fonde toute une théorie mathématiques - au contraire d'un axiome, on ne s'interdit pas de chercher la démonstration d'un postulat) :
1 - Un segment de droite peut être tracé en joignant deux points quelconques.
2 - Un segment de droite peut être prolongé indéfiniment en une ligne droite.
3 - Étant donné un segment de droite quelconque, un cercle peut être tracé en prenant ce segment comme rayon et l'une de ses extrémités comme centre.
4 - Tous les angles droits sont congruents (Celle là, je la comprends pas bien...)
5 - Par un point extérieur à une droite, on peut mener une et une seule parallèle à cette droite.
(A noter que Hilbert passe derrière en 1899, et propose 21 postulats comme base de la géométrie euclidienne... En fait, il y en avait un en trop dedans, mais c'est un détail)

Et pendant de très nombreuses années, les mathématiciens se sont toujours accordés à accepter les quatre premiers postulats (devenant, de fait, un axiome), mais pour le cinquième, ça bloquait... Ils étaient intimement persuadés qu'il était démontrable à partir des quatre premiers.
Et lors de nombreuses recherches infructueuses, ils tentèrent de voir ce que cela donnerait si ce cinquième postulat était faux.

Et si, par un point extérieur à une droite donnée, ne passait aucune droite parallèle ?

Créé par Riemann, cela donne une géométrie elliptique. Au lieu du plan, on évolue sur une sphère, et les droites, ce sont les cercles possédant le même centre que celui de la sphère. Là-dedans, les triangles peuvent (entre autres) avoir trois angles droits...

Par M ne passe aucune droite parallèle à D.

Et si, par un point extérieur à une droite donnée, passent une infinité de parallèles ?

On se retrouve avec une géométrie hyperbolique, crées par Lobatchevsky, Klein ou Poincaré (à des époques différentes). Tout un tas de modèles équivalent existe, mais j'en parlerait surement une autre fois sur le blog. En gros, ça donne quelque chose comme ça :

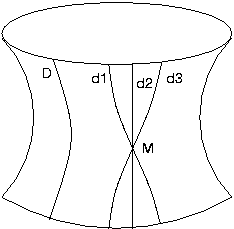
Géométrie hyperbolique de Lobatchevsky : par M passent une infinité de parallèles à D.

Maintenant, vous savez... Ne nous laissons pas dicter la géométrie par Euclide ! Il ne faut pas se laisser faire !

(Surtout qu'aujourd'hui, avec tout les concepts qu'on a inventés depuis, la géométrie euclidienne a laissé sa place à des choses encore plus alambiquées : dimensions infinies, distances négatives ou géométrie fractale).

---

Vous pouvez lire ce passage du Petit Prince ici. A noter que la discussion entre Antoine et Le Petit Prince n'est en réalité pas dans le bouquin du même nom, c'est simplement un hommage par un mathématicien au Petit Prince.
(Et pour les sources, c'est encore Wikipedia, d'où proviennent les deux dernières images).

Comments

[Phoenixx]

C'est dingue ça, le matin du jour où a été postée cette note, j'étais en train d'évoquer ces géométries non euclidiennes dans mon DS de philo ... Et tout à l'heure je pensais même à te donner ces géométries comme sujet d'une note sur ce blog ... C'est dingue non ? Comme quoi, les grands esprits se rencontrent ! C'est bien expliqué en tout cas ... (Faut que je m'en remette)

[blop]

le theoreme du petit prince, il n'est vrai que sur une sphere
Je suis sur que tu peux nous dessiner un triangle non equilateral a 3 angles droits !

[Tipierre]

Ouais bah je préfère me lisser dicter la géométrie par Euclide... Parce qu'avec Riemann, rien que "Tracez un triangle quelconque" ça devient impossible !

[Zetron]

Et le mouton, il a combien d'angles droits ?

[Kaki]

Rôh, moi j'voulais une analyse de la portée philosophique du Petit Prince !

Moi j'aime bien Euclide, en fait, hein...
Mais... J'préfère la géométire fractale, quand même :D

Dis, diiis, tu parles des fractales ? (non, non, je ne me défile pas... ¬¬)