Problèmes antiques
Allez, munissez-vous tous d'un compas, d'une règle et d'un crayon, nous montons dans le bus magique pour l'Antiquité ! Dites au revoir aux fractales, à la théorie des groupes et aux puzzles un brin trop compliqués, là ou nous allons, tout ça n'a pas encore été inventé... La Grèce antique, 5eme siècle avant J-C. On commence à parler de nombres premiers et même d'intégrale, mais ce qui nous intéresse aujourd'hui, ce sont les problèmes de géométrie de l'époque.
J'espère que tout le monde a bien pris sa règle et son compas. Ouvrez bien vos esgourdes, les questions commencent ! Pour plus de compréhension, j'ai écrit les question en français, et non en grec antique.
Problème numéro 1 : la trisection de l'angle
Sur votre feuille, tracez un angle quelconque. Maintenant, à l'aide de votre règle et de votre compas, vous devez diviser cet angle en trois parties égales.
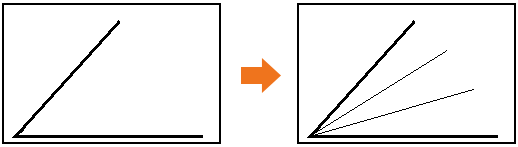
Problème numéro 2 : la quadrature du cercle
Ce petit problème est un peu plus compliqué. Après avoir tracé un cercle quelconque sur votre feuille, vous devez construire un carré de la même aire que ce cercle.
Problème numéro 3 : La duplication du cube
(Cadre historique : pour faire cesser la peste à Athènes, l'oracle de Delphes demande aux Athéniens de doubler l'autel cubique consacré à Apollon)
Après avoir dessiné un cube sur votre feuille (enfin, son patron), vous allez devoir construire le cube qui possède le volume double du premier.
La réponse à ces questions... Après la page de publicité.
=== PubL ===
Ne ratez pas l'article de Choux Romanesco, Vache qui rit et intégrale curviligne de la semaine prochaine, qui donnera les solutions des trois grands problèmes antiques : trisection de l'angle, quadrature du cercle et duplication du cube !
=== /PubL ===
Avant de passer aux réponses, un petit point d'histoire tout de même. Ces trois problèmes de l'antiquité sont appelés les "trois grands problèmes de l'Antiquité" (Nom pas très original, j'admets, même si parfois, on y ajoute un quatrième problème, celui de construire un polygone régulier à n côtés). En fait, les anciens n'ont jamais réussi à trouver leur solution avec leur règle et leur compas, et c'est seulement grâce au développement de l'algèbre que les solutions ont été trouvées.
Les solutions sont simple : il n'y a pas de solution. (Désolé de l'annoncer comme ça, j'espère que vous n'avez pas trop cherché longtemps quand même...)
Il est tout à fait impossible de dupliquer un cube, de trisecter un angle ou de quadraturer un cercle seulement avec une règle et un compas. Pourquoi ? Je vais tâcher d'y répondre tout de suite.
Avant de savoir ce que l'on ne sait pas faire, commençons plutôt par ce que l'on sait faire avec une règle et un compas.
* J'espère que tout le monde sait tracer la parallèle à une droite passant par un point donné, ainsi que la perpendiculaire à une droite passant par un point donné, avec une règle et un compas (pas besoin d'équerre) :
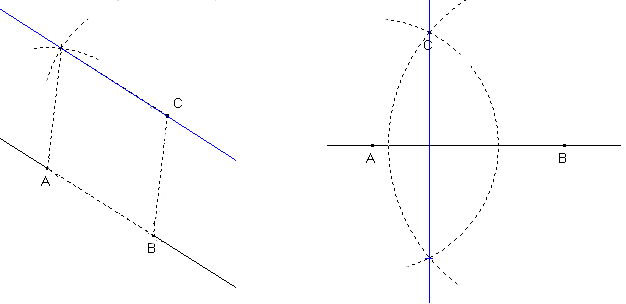
* Plus intéressant : on peut facilement faire des additions et des soustractions de longueurs :
* Et encore plus chouettes, grâce au théorème de Thalès, on peut effectuer des multiplications et des divisions :
* Et le plus chouette encore, l'extraction de racine carrée ! Dans l'image ci-dessous, y=√x :
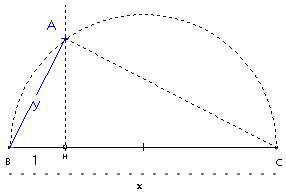
Et en fait, c'est a peu près tout ce que l'on peut faire avec des longueurs : des additions, des soustractions, des multiplications, des divisions et des extractions de racines carrées. Pourvu qu'on ait une longueur unité, on peut construire tout un tas de nombres avec ça. On appelle "ensemble des nombres constructibles" toutes les longueurs que l'on peut construire à partir d'un segment unité, d'une règle et d'un compas. Si deux nombre sont dans cet ensemble, alors leur somme, leur différence, leur produit et leur quotient appartiennent à cet ensemble : on dit que l'ensemble des nombres constructibles est un "corps". De plus, si un nombre appartient à cet ensemble, alors sa racine carrée y est également : on peut dire que l'ensemble des nombres constructible est un corps stable par racine carrée.
Dans les différentes opérations sur les nombres montrées plus haut, je n'ai montré de formidable que l'extraction de racine carrée : pas de racine cubique ou cinquième, par exemple. Et pour cause : c'est impossible. A partir d'un segment unité, on ne peut construire à la règle et au compas que des sommes, différences, produit, quotient et racines carrées de nombre : le corps des entiers constructibles et le plus petit corps stable par racine carrée (Autrement dit : l'ensemble des nombres que l'on peut écrire avec des +, des -, des ×, des ÷ et des √)
On peut voir la même chose d'un autre point de vue : un nombre ne peut être construit à la règle et au compas à une seul condition (qui n'est pas suffisante) : Il doit être la racine d'un polynôme (A coefficients entiers) qui a pour degré une puissance de 2 . Inversement, un nombre qui n'est pas racine d'un polynôme ayant pour degré une puissance de 2 n'est pas constructible à la règle et au compas. (À peu de choses près, c'est le théorème de Wantzel) C'est grâce à cette dernière version du théorème de Wantzel que l'on va pouvoir démontrer l'impossibilité de résolution des 3 grands problèmes antiques.
La duplication du cube
Si on revient à notre problème numéro 3 de duplication du cube. Si on imagine que l'arrête du cube de base mesure 1, son aire vaudra 1. Il faut alors construire un cube ayant pour volume 2, et donc, d'arête égale à 
. Le problème, c'est que ce nombre est la solution de l'équation x3-2=0, qui est une équation de troisième degré (et 3 une puissance de 2). En conclusion, le nombre n'est pas un nombre constructible à la règle et au compas, la duplication du cube sera alors impossible.
La quadrature du cercle
Si notre cercle a un rayon d'une unité, son aire vaudra π (pi). Le carré qu'il faudra alors construire aura alors pour côté √π. Comme on sait extraire des racines carrées, ce n'est pas un problème de construire √π si on sait construire π... Et là est le hic, puisque π est un nombre transcendant, c'est à dire qu'il n'est la racine d'aucun polynôme à coefficient rationnel, donc encore moins d'un polynnôme ayant pour degré une puissance de 2. Pi n'est pas constructible, la quadrature du cercle est donc impossible !
Trisection de l'angle
(Là, l'explication est déjà un peu plus ardue, et pas très précise, mais c'est l'idée)
Si notre angle de départ est α, on peut très facilement construire cos(α) (On trace le cercle unité, et on prend le projeté orthogonal de l'intersection cercle/droite sur l'autre droite). Pour trouver la trisection du cercle, il va falloir réussir à tracer cos(α/3).
En s'amusant un peu avec nos chères relations de trigonométrie, on trouve que cos(α)=4.cos3(α/3)-3.cos(α/3), soit une équation de la forme a=4x3-3x. L'équation à résoudre est alors du troisième degré, et sauf dans de rares cas, les solutions seront pleines de racines cubiques. En gros, cos(α/3) n'est pas un nombre constructible, et c'est bien dommage !
Bref, à la règle et au compas, ces trois problèmes de la Grèce antique sont absolument impossible. Mais il existe heureusement d'autres méthodes astucieuses !... (Suspens jusqu'à la semaine prochaine...)
Source :
Beaucoup trop de wikipédia (dont sont issues toutes les images de la deuxième partie)
Et un peu de l'encyclopédie de Gérard Villemin.
/http%3A%2F%2Fstorage.canalblog.com%2F77%2F73%2F210892%2F111515552_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F43%2F78%2F210892%2F106322231_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F16%2F78%2F210892%2F106207701_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F63%2F97%2F210892%2F99779882_o.png)