Tête de Mohr

Rappelez-vous, les deux dernières fois, je vous ai parlé de tout ce qui était faisable (et pas faisable) grâce au merveilleux couple antique du compas et de la règle non graduée. Même si on ne peut pas couper un angle en trois au compas et à la règle, il y a tout un tas de choses que l'on peut faire : couper un angle en deux, tracer des parallèles, des perpendiculaires, des triangles équilatéraux, des carrés, voire même faire des additions, multiplications ou extractions de racines carrées...
Mais la règle non graduée n'a rien de magique, ne permet de tracer que de vulgaires traits. Alors que le compas, lui, est beaucoup plus dansant, permet de tracer de belles courbes (enfin, seulement des cercles). La question que l'on est en droit de se poser est alors celle-ci : que se passe t'il si l'on se sépare de sa règle, et que l'on garde uniquement le compas ?

Et bien, Georg Mohr découvre en 1672 que pour faire des constructions à la règle et au compas, la règle ne sert absolument à rien ! (A l'époque, l'information est passée totalement inaperçue, il a fallut attendre 1797 pour qu'un autre mathématicien, Mascheroni, découvre à nouveau que la règle est superflue. Il a dans la foulée découvert que ça avait déjà été découvert)

Bon, évidemment, on ne pourra jamais faire de droite avec un compas seul, mais on peut les imaginée tracées lorsque deux points de cette droite sont déjà tracées.

Le théorème de Mohr est bien joli dans la théorie, mais dans la pratique, comment ça marche ? Comment faire dans la réalité pour faire cet exercice de géométrie alors qu'un malotru vient de briser votre règle réputée incassable ?

Exercice numéro un : La rosace !
(Réalisable par n'importe quel cancre s'ennuyant au fond de la classe, avec un compas entre les mains)
Soit deux points sur la feuille. Réaliser le symétrique du premier point par rapport au deuxième. Dans la foulée, réaliser un triangle équilatéral et un hexagone régulier...
La solution est simple, et plus connue sous le nom de rosace ! (Que le premier qui n'a jamais dessiné de rosace sur ses feuilles de cours me jette la première pierre... Aïe !)

Exercice numéro deux : Question n°641
Réaliser un carré seulement à l'aide d'un compas ! (A partir de deux points quelconques)

Après de nombreuses heures de recherches, voici enfin la réponse à la question n°641 de ce questionnaire !

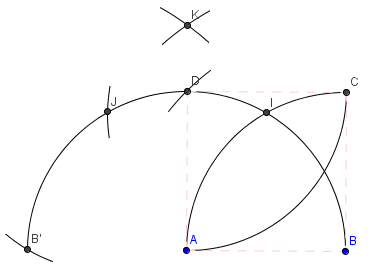
A partir des points A et B, on construit I, J et B', avec la technique de tracé de la rosace.
Les deux cercles de centre B et B' de rayon BJ se coupent au point K.
En prenant la longueur de compas AK, on trace le cercle de centre B. On obtient alors le point D, entre I et J.  Ce qui est dingue la dedans, c'est que (AB) et (AD) sont perpendiculaires.
Il n'y a plus qu'à tracer C, le dernier point du carré, en prenant le symétrique de A par rapport à (BD).

Exercice numéro trois : La construction de Napoléon
La centre d'un cercle a été perdu. Saurez-vous le retrouver en utilisant seulement un compas ?
Pourquoi ce problème porte t'il le nom de Napoléon ? La réponse tout de suite :
A son retour de la campagne d'Italie, Napoléon Bonaparte parla à l'Académie des sciences des travaux du mathématicien italien Mascheroni, et notamment de ce problème du centre perdu. Laplace aurait alors répondu "Nous attendions tout de vous, général, sauf des leçons de géométrie".

Maintenant, la résolution du problème, assez laborieuse :
Le cercle c est tracé (en rouge). On prend alors un point quelconque P dessus, et on trace un cercle quelconque c', qui coupera c en deux points A et B.
A partir de ces deux points, on trace deux nouveaux cercles de rayons AP, et ils se coupent au point C.
Ce point C est le centre d'un nouveau cercle de rayon PC, qui coupe c' en deux points, E et D.
On trace alors les cercles de centre E et D, de rayon EP. Ceux-ci se couperont au centre du cercle de base !

Exercice numéro 4 : le milieu
Trouver à la règle et au compas le milieu d'un segment est plutôt facile, mais saurez-vous le retrouver au compas seul !

Avant de regarder la réponse, cherchez !

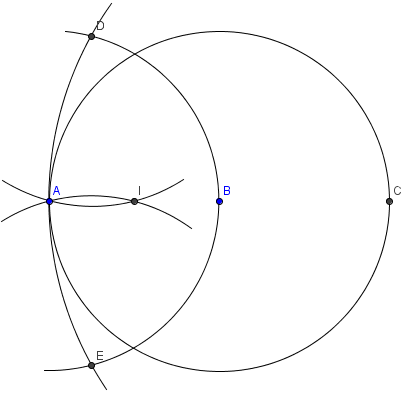
On va tenter de construire le milieu de [AB]. Avec la technique de la rosace, on construit C, symétrique de A par rapport à B.
On construit alors le cercle de centre A de rayon Ab et le cercle de centre C de rayon AC. Ces deux cercles se coupent en D et E.
A partir de D et E, on construit les cercles de rayons AD.  Ces deux cercles se coupent en I, qui n'est autre que le centre de [AB].
 

Tout ça pour dire que pour la rentrée, cela ne sert à rien d'acheter de règle ou d'équerre, un simple compas permet de tout faire ! (Avec plus ou moins de difficultés... Les opérations sur les longueurs présentées il y a deux semaines (additions, multiplications...) sont bien sûr faisables, mais encore plus ardues. Si cela vous intéresse vraiment, il vaut mieux aller voir les liens.)

---

Sources :
La page personnelle de Baptise Gorin, et son article sur le théorème de Mohr. (Avec tout ce qu'il faut pour comprendre à fond)

Comments

[nico]

j'ai cherché pas mal de temps la solution a la question n°641 et j'ai enfin la solution ,mais elle ne vien pas de moi ,domage et merci

petit exercice pour toi:
a l'aide d'une regle non graduée et d'un crayon
un segment AB et une parallele a ce segment
diviser le segment AB en 3 parties egales

certainement facile pour toi mais moi j'aime bien

[luciolette]

Merci pour l'explication concernant le milieu d'un segment en utilisant uniquement le compas ! Trop cool

[martin Lothar]

On ne saurait trop le dire : Le compas est un des outils qui permet de fonder une civilisation et de résoudre bien des quadratures du cercle infernal de l'infâme Docteur Pi. Il est du bon côté de la force.
Il y a d'autres outils bien sûr, mais ça c'est une autre histoire que je vous raconterai si vous êtes sages. A+

[Tipierre]

J'ai jamais vu d'explication aussi compliquée pour faire une rosace ^^
Et j'adore la construction de Napoléon ! La dernière aussi est interessante...