Choux romanesco, Vache qui rit et intégrales curvilignes

C'est pas de la tarte

Bientôt les fêtes, et qui dit fête dit gâteau festif. Comme la bûche, c'est pas bon, c'est année, le gâteau du réveillon sera une délicieuse tarte aux litchis !... Vingt invités sont présents, tout le monde aime les litchis ?... Non ? Y'en a trois qui n'aiment pas... Ah... Va donc falloir couper la tarte en 17 parts égales...
Voyons voir, 17, c'est bien un nombre premier de Fermat ? Alors parfait, ça devrait être faisable, tout le monde va avoir sa part de tarte aux litchis !

Tout bon coupeur de tarte, comme tout bon géomètre grec, doit savoir s'armer des deux objets de base de la découpe de tarte : la règle et le compas ! Avec ça, découper une tarte aux litchis en 3, 4, 5, 6 ou 17 parts égales deviendra un jeu d'enfant !

Le triangle équilatéral et l'hexagone régulier
Couper un cercle en 3 ou 6 parts, tout le monde sait faire ça, sinon, j'ai honte de ce que l'on a pu vous apprendre à l'école. On prend le rayon du cercle, on le reporte 6 fois sur les côtés, et on obtient un bel hexagone. En ne prenant qu'un point sur 2, c'est une chouette triangle équilatéral que l'on obtient.

Le pentagone régulier
Là, les choses se compliquent. Si vous avez un quart d'heure devant vous, vous pouvez tenter d'inscrire un pentagone régulier dans un cercle, la chose est loin d'être aisée.
...
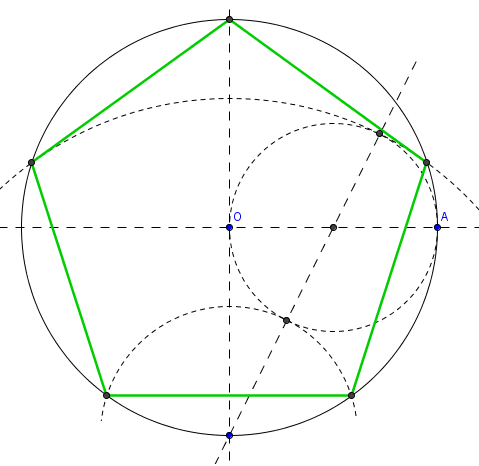
C'est bon, la demie-heure est passée ? Voici donc la solution (on ne peut moins rigoureuse dans la forme):
- On commence par tracer deux diamètres perpendiculaires du cercle.
- On trouve ensuite le milieu de [OA], et on trace le cercle c qui va avec.
- On trace ensuite la droite qui va bien passant par ce cercle et le point B (c'est celui qui est tout en bas)
- Cette droite coupe notre cercle c en deux endroits. Il ne reste que les arcs de centre B passant par ces points, et le tour est joué.

L'heptadécagone régulier (pour notre tarte aux litchis)
Et notre tarte à découper en 17, dans cette histoire ? On y arrive ! Si vous avez quelques heures devant vous, vous pouvez également chercher comment couper un cercle en 17 parts égales. Gauss l'a bien trouvé, lui... Si vous n'avez pas le courage de chercher voici la solution magique :

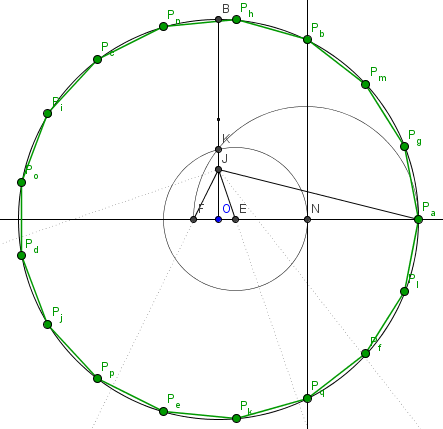
- Notre cercle est de rayon O, on lui construit deux beaux diamètres orthogonaux [OP_a] et [OB].
- On construit le point J au quart de [OB]
- On relie élégamment J à P_a.
- On construit le point E sur (OP_a) de manière à ce que l'angle OJE soit le quart de OJP_a (Grâce à la magie des bissectrices)
- On construit ensuite le point F sur (OP_a) de manière à ce que l'angle FJE soit 45° (Perpendiculaire + Bissectrice)
- On construit le demi cercle qui passe par F et P_a, qui coupe [OB] en K.
- Le cercle de centre E passant par K coupe (OP_a) en N.
- Il n'y a plus qu'à tracer la perpendiculaire de (OP_a) passant par N, et on trouve le point P_b.
- On reporte ensuite la longueur P_aP_b pour trouver P_c, et ainsi de suite jusqu'à P_q.
- Servez chaud.

Et pour avoir un décagone (10 côtés) ?
On sait déjà couper en 2, 3, 5 et 17. En divisant toute les part en 2 dans tous ces cas, on peut très facilement couper notre tarte en 6, 10, 12, 20, 24 ou 34...
Si on sait couper une tarte en n côtés, la couper en 2^k.n côtés est donc quelque chose de facile à faire.

Et pour le pentadécagone (15 côtés) ?
On sait faire un découpage en 3, et on sait le faire en 5. Comme par hasard, ces deux nombres sont premiers entre eux (aucun diviseurs commun). Une petite application du théorème de Bézout permet de dire que puisque 3 et 5 sont premier entre eux, il sera possible de couper la tarte en 3×5, en reportant autant de fois que nécessaire la distance entre un point du triangle et un point du pentagone :

Finalement
- si on sait couper notre tarte en n parts
- si on sait couper notre tarte en m parts
- si n et m sont premiers entre eux
Et bien, on peut couper notre tarte en n×m
Et donc, on peut la couper en 2^k.n.m (d'après le paragraphe précédent)
Couper une tarte en 2, 3, 4, 5, 6, 8, 10, 12, 16, 17 ou 20 est donc d'une simplicité déconcertante (enfin, c'est faisable de manière ultra précise)

L'heptagone
Sur les 17 invités, il y en avait en fait 10 qui ne connaissaient pas les litchis, et sont en fait plutôt tentés par la bûche de Noël. Notre tarte au litchi, déjà bien abimée, doit donc être découpée en 7... Question à 20 centimes d'euros : comment faire un heptagone régulier ?...

Et c'est là que la réalité nous rattrape... Pour que l'on puisse couper une tarte en un nombre premier de côté (supérieur à 3), il faut que ce nombre premier soit un nombre premier de Fermat, c'est à dire, un nombre premier de la forme p=1+2^(2ⁿ). (Pour la démo, va falloir lire les sources...) Les premiers de ces nombres sont 3, 5, 17, 257 et 65537. (Mais 4 294 967 297 ne compte pas, il est divisible par 641... Actuellement, on ne sait pas s'il existe des nombres premiers de Fermat plus grand que 65537). En tout cas, le 257-gone et le 65537-gone sont constructibles, mais j'ai déjà assez galéré avec 17 côtés pour en faire 257. (Mais les constructions existent belles et bien ; Richelot et Schwendenwein ont fait un 257-gone en 1832, et Hermes a passé 10 ans à la construction d'un 65537-gone dans les années 1900)

Moralité :
Pour partager une tarte aux litchis en n parts, il faut donc absolument pouvoir écrire n=2^kp₁...p_l, avec p_i des nombres premiers de Fermat tous différents. (Tel est le théorème de Gauss-Wantzel)

La semaine prochaine, nous verrons quel est le rapport entre la trigonométrie et une tarte aux yuzus, et comment on peut malgré tout découper une tarte aux yuzus en 9 parts égales...

NB :
Cela marche aussi très bien avec les pizzas aux litchis.

Sources :
Construction des polygones réguliers [pdf] (toutes les démonstrations nécessaires)
Construction de l'heptadécagone régulier,
Quelques infos sur le 257-gone et le 65537-gone que j'ai pas réussi à placer (Mais je cherche toujours leur programme de construction)