Fractales ?
Concrètement, une fractale (ou, un "objet fractal", à l'origine, c'est un adjectif), c'est quoi ? ...
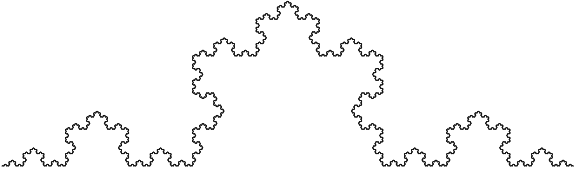
La courbe de Koch : on part d'un segment, on construit un triangle équilatéral sur le tiers central, et on répète indéfiniment le processus sur les nouveaux segments.
... Le mot fractal (du latin fractus, qui signifié brisé) a été inventé par Benoît Mandelbrot (Les Objets fractals : forme, hasard, et dimension, 1973.)...

Le triangle de Sierpiński : on part d'un triangle (équilatéral) auquel on évide la partie centrale. On obtient 3 triangles, sur lesquels on répète le même processus d'évidement de la partie centrale.
... Mais Mandelbrot n'y donne en fait pas vraiment de définition de ce que signifie "fractal"...

La baderne d'Apollonius : après avoir construit un grand cercle et 3 cercles tangents les uns aux autres, on construit de nouveaux cercles de manière à ce qu'ils soient toujours tangents à 3 autres cercles.
... Une chose est sûr : la caractéristique d'une courbe ou d'une surface fractale, c'est d'être irrégulière ! ...

Un ensemble de Julia (de paramètre -0.38) : les points en noirs possèdent une caractéristique propre, que ne possèdent pas les points colorés. Cette caractéristique a rapport avec les nombres complexes. (Je m'y attarderai bien plus dans quelques semaines)
... Enfin, tout dépend de ce que l'on appelle "irrégulier" ! (Personnellement, je trouve la courbe de Koch très régulière, dans son genre). Ce qu'il nous faut en plus de l'irrégularité, c'est de posséder des homothéties internes...

L'ensemble de Mandelbrot : Très proche des ensembles de Julia, on le définit également à partir des nombres complexes. (Je m'y attarderai bien plus dans quelques semaines)
... Dans le langage un peu plus courant, on dit volontiers "zoom" ou "dézoom" pour parler des homothéties. Un objet est fractal lorsque, quand on le regarde de plus près, il reste à peu près le même : il est autosimilaire...

Un mouvement brownien : imaginez un grain de pollen en suspension dans l'eau. Les molécules d'eau sont en perpétuel mouvement, ils leur arrivent donc de frapper ce grain de pollen, un mouvement en résulte. Ce mouvement dans tous les sens, complètement hasardeux, est un mouvement brownien.
... Les plus simples des fractales utilisent des processus déterministes : une recette permettant d'aboutir (après un nombre infini d'étapes) à une -jolie- figure géométrique. La courbe de Koch et le triangle de Sierpiński utilisent la géométrie basique, les ensembles de Julia ou de Mandelbrot utilisent des concepts plus avancées comme les nombres complexes, mais restent le résultat d'une recette...

L'évolution du CAC40 : Quand on pense à une courbe très irrégulière, c'est généralement à celle de la bourse que l'on pense, qui présente tous les traits d'une courbe fractale.
... D'autres fractales sont fabriquées en utilisant des processus stochastiques, c'est à dire, à base d'aléatoire. Un mouvement brownien ou une courbe de la Bourse font partie de ce genre de courbes fractales...
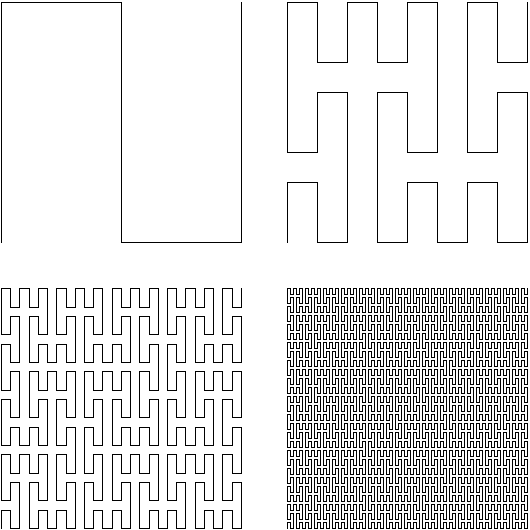
La courbe de Peano (4 premières étapes de dessin) : Étape 1 - Dessinez une grille 3×3, puis dessinez une courbe passant par toutes les cases, joignant celle en bas à gauche à celle en haut à gauche (Le chemin trouvé ressemble à un N). Étape 2 : chaque cellule de la grille est à nouveau divisée en 9, et on effectue les mêmes trajet en N dans ces nouvelles divisions. En répétant le processus à l'infini, on trouve la courbe de Peano (indessinable, l'épaisseur du trait donnerait un carré noir)
... La grande particularité des fractales, c'est d'être toujours à mi chemin entre la 1ère dimension et la 2eme dimension. Nous vivons dans un monde en 3 dimensions ; une surface (une feuille de papier, plus ou moins pliée) est à 2 dimensions ; une courbe (un trait dessiné sur cette feuille) ne possède qu'une dimension. La courbe de Peano est une courbe -donc, à 1 dimension- mais finit par recouvrir entièrement un carré, qui lui, est à 2 dimension. Une ou deux dimensions ? Cette indécision est la caractéristique principale des fractales...
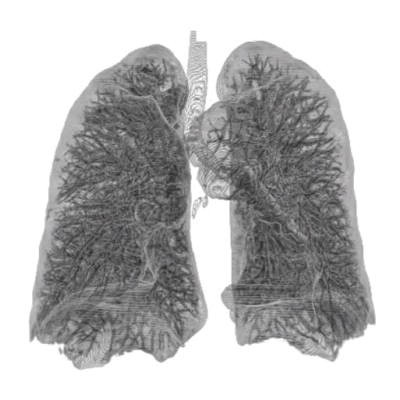
Des poumons : Les échanges gazeux entre l'air et le sang se font dans les alvéoles pulmonaires. Pour multiplier le nombre d'alvéole et faciliter les échanges, les conduits alvéolaires présentent une structure arborescente (fractale). La surface d'échange contenue dans deux poumons est alors comparable à la taille d'un court de tennis.
... Finalement, pour définir exactement tout ce que l'on range dans la catégorie fractale, il faut s'intéresser à cette histoire de dimensions. C'est pourquoi on appelle "fractale" un ensemble dont la dimension de Hausdorff est strictement supérieure à la dimension topologique...

L'éponge de Menger : Il est construit de la même façon que le triangle de Sierpiński. On part d'un cube subdivisé en 27, et on évide les parties centrales. Il reste alors 20 cubes, sur lesquels on réitère le processus, et ainsi de suite.
... C'est quand même plus précis que "une fractale est un objet mathématique qui contient des fractales", mais ça nécessite beaucoup plus d'explications qu'une simple suite de de dessins comme dans l'article d'aujourd'hui. Mais les explications à propos de cette histoire de dimension seront pour la semaine prochaine !

Art fractal (Michael Michelitsch - 1990) : Grâce à l'informatique, on a pu obtenir facilement des illustrations de fractales, mais une nouvelle discipline artistique est également apparue. Quand l'art s'empare des mathématiques, cela donne le fractal art contest de Benoit Mandelbrot.
Sources :
Wikipédia, d'où proviennent l'ensemble des illustrations. (Sauf celle de la bourse, qui vient de Yahoo!)



/http%3A%2F%2Fstorage.canalblog.com%2F84%2F61%2F210892%2F116475097_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F20%2F79%2F210892%2F104082950_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F49%2F06%2F210892%2F98803495_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F86%2F89%2F210892%2F85831746_o.png)