M le maudit

Aujourd'hui, place à la plus célèbre des fractales... L'ensemble de Mandelbrot !

Mais, l'ensemble de Mandelbrot, kessécé ?
C'est "L'ensemble des points c du plan complexe tels que la suite définie par z_n+1 = z_n² + c, avec z₀=0, ne diverge pas en module".
Comme c'est pas super clair dit comme ça, détaillons un petit peu.

Les nombres complexes
(Normalement, bien connus à partir de la terminale)
Un nombre complexe est un nombre z de la forme z=a+ib, avec i l'unité imaginaire (telle que i²=-1). Soit.
Le plus grand intérêt des nombres complexes, c'est qu'on peut les représenter facilement graphiquement dans le plan complexe. Par exemple, le nombre complexe z=2+i se représente dans le plan complexe ainsi :

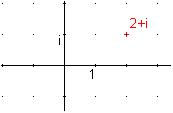
Deuxième intérêt des nombres complexes : on peut les additionner et les multiplier.
Si on a z=a+i.b et z'=a'+i.b', on a alors :
z+z' = (a+a') + i.(b+b')
z.z' = (a.a' - b.b') + i.(a.b' + a'.b)
z² = (a²-b²) + 2iab

Le module d'un nombre complexe z, noté |z|, est sa distance à 0 dans le plan complexe. On le calcule par la formule z²=a²+b² (Pythagore).

Les points de l'ensemble de Mandelbrot
Sur la représentation plus haut, l'ensemble de Mandelbrot, c'est l'ensemble des points noirs du dessins.

Prenons un point c du plan complexe ; doit-on le colorier en noir ou pas ? Pour le savoir, il faut calculer la suite définie par z_n+1 = z_n² + c, avec z₀=0.
Si cette suite ne part pas vers l'infini, le point sera dans l'ensemble de Mandelbrot.

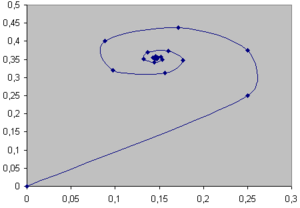Prenons par exemple le point c=0.25 +i. 0.25 :
z₀ = 0
z₁ = z₀² + c = 0² + 0.25 + i. 0.25 = 0.25 + i. 0.25
z₂ = z₁² + c = (0.25 + i. 0.25)²+(0.25 + i. 0.25) = 0.25 + i. 0.375
z₃ = 0.171875 + i. 0.4375
z₄ = 0.08813477 + i. 0.40039063
...

En calculant un grand nombre de valeur de cette suite, on s'aperçoit qu'elle s'approche de plus en plus d'une certaine valeur, et donc, ne part pas vers l'infini. Ce point est bien dans l'ensemble de Mandelbrot !

Un autre exemple : c= 1 + i
z₀ = 0
z₁ = 1 + i
z₂ = 1 + 3.i
z₂ = -7 + 7.i
z₂ = 1 - 97.i
...

En continuant, on s'aperçoit que les point s'éloignent de plus en plus de 0. On dit que la suite diverge en module (la suite diverge en module lorsque le module tend vers l'infini). Le point 1+i ne fait donc pas parti de l'ensemble de Mandelbrot !

Dessiner l'ensemble de Mandelbrot
Ca, c'est la partie théorique, mais dans la pratique, comment fait-on pour obtenir un beau dessin ?

L'idée, c'est de découper l'écran en pixels, à chaque pixel correspondant un nombre complexe. Pour chaque pixel, il faut savoir si la suite (z_n) converge ou non en module. Le problème est que pour savoir ça, il faudrait calculer une infinité de termes de la suite, ce qui est impossible pour un ordinateur !
Une seule chose est sûre quand même : si la suite sort du cercle de centre 0 et de rayon 2, alors, elle divergera. Autrement dit : si à partir d'un certain rang, le module de z_n est plus grand que 2, on est sûr que la suite n'appartient pas à l'ensemble de Mandelbrot.

Pour chaque pixel, donc, on calcule les 100* premiers termes de la suite (z_n), ainsi que leur module. Si, au bout de 100 itérations de la formule z_n+1 = z_n² + c, le module est toujours inférieur à 2, on considère qu'il ne dépassera jamais 2, et le pixel sera colorié en noir.

* On peut remplacer 100 par un autre nombre. Plus ce nombres est grand, plus l'image sera précise !

Ca, c'est pour l'intérieur de l'ensemble de Mandelbrot.
Pour colorier l'extérieur de l'ensemble de Mandelbrot, on s'intéresse au nombre d'itérations nécessaires pour que la suite dépasse 2 en module.

Visite presque guidée de l'ensemble de Mandelbrot

Mais le plus important dans l'ensemble de Mandelbort, c'est que malgré sa -relative- simplicité (ça ne fait intervenir qu'une mise au carré et une addition...), il est d'une complexité infinie, et on peut retrouver toutes sortes de motifs.

Ci-dessus, l'ensemble de Mandelbrot, comme tout en haut, mais avec un aura orange. e ce point de vue, l'ensemble est surtout composée d'une cardioide et de cercles.


Zoom autour du point (-1.75, 0).
On remarque le trait caractéristique des fractales : l'autosimilarité à toutes échelles.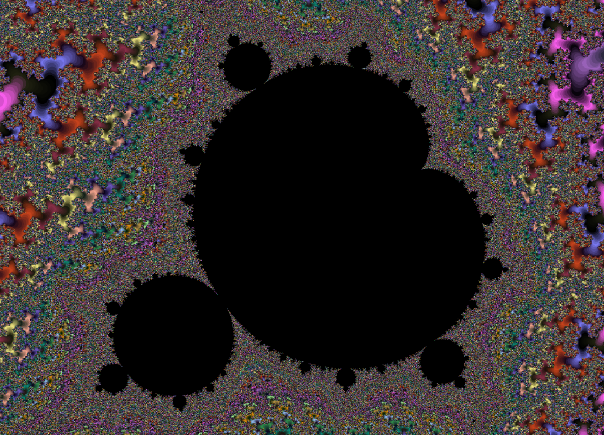

---

Sources :
Toutes les images ont été faite avec le logiciel XaoS

Comments

[luxtin]

Très intéressant et très joli !