Mandelbrot et ses Julias

L'ensemble de Mandelbrot trône en roi sur le monde des fractales : une définition simple comparée à la complexité du résultat. Mais les prétendants sont en nombre, et guettent le siège. Petite présentation de l'entourage très proche de l'ensemble de Mandelbrot !

Petit rappel, en quelques mots : l'ensemble de Mandelbrot, c'est
* l'ensemble des points c du plan complexe
* telle que la suite z_n+1 = z_n² + c ne diverge pas
* avec z₀=0

Changement de terme initial
Pour chaque c, on considère une suite commençant par z₀=0. Comme n'importe quel choix arbitraire, on peut le changer !

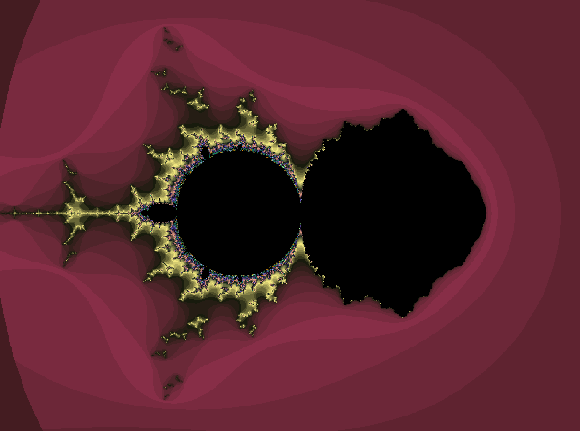
z₀=1

z₀=0.5

z₀=0.5i

z₀=i

Les ensembles de Julia
Mandelbrot, c'est : pour un z₀ donné, on s'intéresse aux c qui ne divergent pas.
Et si on faisait l'inverse ? Pour un c donné, on regarde tous les z₀ qui ne divergent pas .

C'est ainsi que les ensembles de Julia (du mathématicien français Gaston Julia) se définissent :
* on choisit un point c (dans l'ensemble de Mandelbrot, ou en dehors, suivant le résultat que l'on souhaite)
* pour chaque point z₀ du plan complexe, on calcule la suite (z_n) définie par z_n+1=z_n²+c
* si la suite (z_n) ne diverge pas, c'est que le point z₀ appartient à l'ensemble de Julia de paramètre c.

L'ensemble de Mandelbrot est devient une sorte de carte des ensembles de Julia : si le paramètre c choisit est dans l'ensemble de Mandelbrot (cas 1, 2, 3 et 4), le point (0,0) sera dans l'ensemble de Julia, ce qui entrainera un ensemble de Julia connexe ("en un seul morceau"). si le paramètre c est en dehors de l'ensemble de Mandelbrot (cas 5), l'ensemble de Julia sera un ensemble de points isolés (de type poussières de Cantor)
De la même façon que pour les ensembles de Mandelbrot, on peut associer une coloration aux nombre d'itérations nécessaires de la suite pour atteindre une valeur d'échappement.

1 : c = 0.25

2 : c = -1

3 : c = -0.15 + 0.75 i

4 : c = -0.62 + 0.43 i

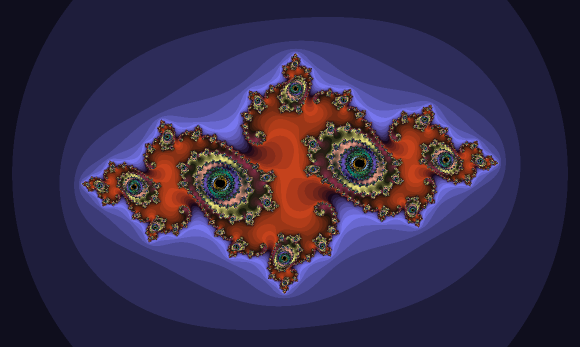
5 : c = -0.75 + 0.145 i
(On ne devrait théoriquement pas observer de si grosses zones noires, mais simplement des points noirs isolés - cela vient du trop petit nombre d'itérations de l'algorithme utilisé)

---

Sources :
Toutes les images ont été faite avec le logiciel XaoS

Comments

[El Jj]

Ce ne sont pas vraiment les fractales qui ont été inventé par Mandelbrot, mais c'est le premier à avoir réuni sous le même terme "fractal" qu'il a inventé les poussières de Cantor (créé pour avoir un exemple simple d'ensemble indénombrable de mesure nulle), les ensembles de Julia (qui ne se limitent en fait pas du tout à ceux exposé dans cet article, crées dans le cadre des systèmes dynamiques), le triangle de Sierpinski ou la côte de Bretagne.

[Tom Roud]

Une question que je me suis toujours posée ... Car Gaston Julia est bien bien antérieur à Mandelbrot, non ? Pourquoi donc attribue-t-on la paternité des fractales à Mandelbrot ?

Sinon, notons que les fractales sont une spécialité française ! Cocorico !