Mandelbrot et ses potes

... suite de l'article précédent...

Changement de formule
L'ensemble de Mandelbrot est donné par la formule z_n+1 = z_n² + c . Et si on change cette formule, qu'est ce qu'il se passe ?
Petite galerie de portrait des cousins proches de Mandelbrot !

Dans la famille Multibrot
Le plus simple des changements à effectuer dans la formule, c'est remplacer 2 par un autre nombre. Avec des entiers supérieurs à 2, on obtient les ensembles de Multibrot.

z_n+1=z_n³+c

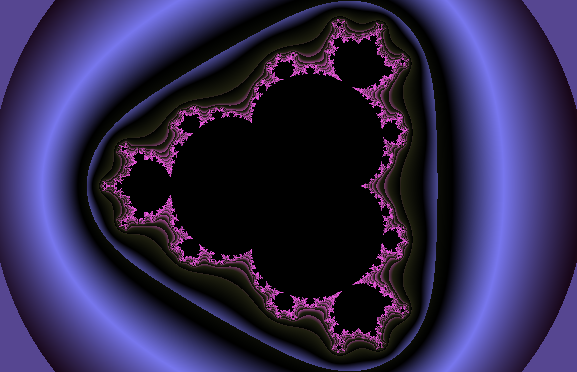
z_n+1=z_n⁴+c

z_n+1=z_n⁵+c

z_n+1=z_n¹⁷+c

Dans la famille puissance négative
Les puissances positives, c'est bien, les puissances négatives, c'est mieux ! (A condition de ne pas commencer la suite des z_n par 0 mais par c)

z_n+1=z_n^-2+c

z_n+1=z_n^-3+c

z_n+1=z_n^-7+c

Dans la famille Mandelbar
Cette fois, on va faire intervenir dans nos calculs le conjugaison d'un nombre complexe. Si z=a+ib, on note z le conjugué de z, et on a z=a-ib. On remplaçant z par z dans la formule donnant l'ensemble de Mandelbrot, on retrouve le tricorne, alias ensemble de Mandelbar.

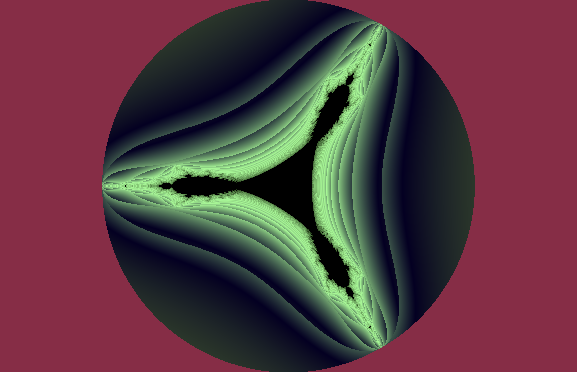
Le tricorne : z_n+1=z_n²+c

z_n+1=z_n³+c

Dans la famille Burning ship
Si notre nombre complexe est de la forme z=a+ib, on note Re(z) la partie réelle de z (Re(z)=a) et Im(z) sa partie imaginaire (Im(z)=b). Si x est un réel, on note |x| sa valeur absolue, qui vaut x si x>0 et -x si x<0. A partir de ces 3 fonctions, on trouve une variante (tordue dans sa définition) beaucoup plus éloigné du Mandelbrot d'origine : la fractale du navire brûlant (Je me permet de baptiser en français cette fractale pour l'occasion !)

Burning Ship fractal : z_n+1 = [|Re(z_n)| + i.|Im(z_n)|]² + c

Zoom sur la fractale (en bas, à gauche)

Dans la famille "Dessinons des bonshommes avec des formules bizarres"
En mélangeant un peu tout ça, et avec un logiciel comme XaoS, on peut tester tout un tas de formule, et avancer encore un peu plus dans la quête ultime de tout enfant de 5 ans : dessiner un bonhomme !

A gauche, nous avons madame z_n+1 = [|Re(z_n)| - i.Im(z_n)]³ - i.c
A droite, nous avons monsieur z_n+1 = [|Re(z_n)| - i.Im(z_n)]⁵ - i.c

Comments

[Tipierre]

Superbe, le burning ship !

[PP?]

Décidément, j'adore les fractales... comme Tût-tûûût, je devine un bâtiment dans l'image zoomée, ça me fait plus penser à une abbaye style Westminster :D
Celles de la famille Multibrot ressemblent à des napperons au crochet, quant aux fractales de la famille négative, elles ressemblent à des pubs pour la St-Valentin (je ne sais pas si je suis très claire :D)
Voilà, c'était le commentaire constructif du jour ;-)

[El Jj]

Tom Roud > Il y a bien rapport entre le groupe de symétrie de l'ensemble de Multibrot avec son exposant : on remarque que si c appartient à l'ensemble d'exposant p (entier), alors c'=c.exp[2.i.pi/(p-1)] y appartient aussi, car on a zn'=zn.exp[2.i.pi/(p-1)].

Quand on passe à des exposants non entiers, il faut affiner la définition de la puissance, en passant par l'exponentielle et les log complexes... Or la démonstration utilise (a^b)^c=a^bc, qui n'est plus vrai avec de telles exponentiations. Conclusion : pas de groupe de symétrie d'angle aussi petit que l'on veut !

En fait, avec des exposants intermédiaires, on trouve des ensembles intermédiaires : l'application qui a un exposant associe son ensemble de Multibrot est continue. La seule symétrie toujours présente, c'est la symétrie axiale.

Gé > Le titre du blog, c'est plutôt en rapport avec le légume ! Le Choux romanesco est une fractale naturelle, mais n'a pas tant de chose à voir avec Mandelbrot.

[Gé]

Choux romanesco, c'est le surnom de l'équation de Mandelbrot ?

[Tût-tûûût]

Le zoom sur la fractale en bas à gauche fait pas mal "cathédrale fantôme". Ça en jette aussi, comme nom.

Sinon, j'adore la conclusion sur les bonhommes :D