Toute la force de Newton

30 août 2008

Toujours dans les fractales, un peu plus éloigné de Mandelbrot, mais tellement joli : les fractales de Newton ! Le nom de cette fractale vient de la méthode de Newton, inventée par Isaac Newton, le même qui a trouvé les lois de la gravitation dans une pomme.

Newton

Fractale de Newton associé au polynôme X³-1

La méthode de Newton
Un pan des mathématiques consiste à faire des calculs exacts, l'autre pan à faire des calculs approchés. Ce deuxième pan, ce sont les méthodes numériques, dans lesquelles on s'amuse généralement à trouver les meilleurs moyen de calculer un tas de décimales de pi ou de.
Prenons le cas de, qui vaut approximativement 1,4142135... Comment a t-on trouvé cette valeur ? Une façon de retrouver ces décimales est la méthode de Newton.

Pour une fonction f donnée (un polynôme, par exemple), la méthode de Newton permet de retrouver ses racines (les x tels que f(x)=0). Le principe de cette méthode est d'approcher la fonction par ses tangentes.
Prenons par exemple la fonction f:x->x²-2.

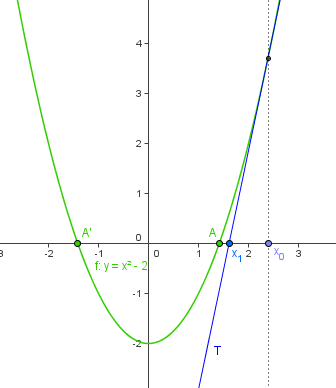
methode

On connait ses racines, c'est (le point A) et - (le point A'). On va alors approcher l'un de ses deux points, de manière à avoir toujours plus de décimales.

On va alors prendre un point quelconque x₀ et tracer la tangente à la courbe au point (x₀,f(x₀)). On peut alors trouver l'abscisse du point x₁, croisement entre la tangente et l'axe horizontal. En recommençant avec le point x₁, on se rapproche du point A, que l'on recherche.

La suite des points x_n se rapproche du point A que l'on cherche, cette suite est donnée par la formule (que l'on trouve par calculs) :

Avec la fonction f:x²-2 et en partant de x₀ = 2, la formule devient .
x₀ = 2
x₁ = 1,5
x₂ = 1,416666667
x₃ = 1,414215686
x₄ = 1,414213562

En 4 itérations, on a déjà au moins 9 décimales correctes !

Choix des termes initiaux
En partant de n'importe quel valeur x₀ positive, on aboutit après plus ou moins d'itérations à ; si on avait choisit une valeur de départ x₀ négative, on aurait aboutit à -.
On peut séparer les valeurs possibles de x₀ en 3 catégories : celles qui aboutissent à , celles qui aboutissent à - et celles qui n'aboutissent nulle part (ici, il n'y a que x₀=0).

Prenons à présent la fonction f:x->x³-3x²+2x. Ce polynôme admet 3 racines : 0, 1 et 2.
Que se passe t'il lorsque l'on applique la méthode de newton en partant de x₀ = 0,4 ? En partant de x₀ = 0,5 ? En partant de x₀ = 0,6 ? De x₀ = 0,5527 ? De x₀ = 0,55275 ? De x₀ = 0,5528 ?

Solutions :
x₀ = 0,4 -> 0
x₀ = 0,5 -> 2
x₀ = 0,6 -> 1

x₀ = 0,5527 -> 0
x₀ = 0,55275 -> 2
x₀ = 0,5528 -> 1

En choisissant une couleur par limite possible (0:jaune, 1:vert et 2:bleu), on retrouve quelque chose de fractal !

$frac_x3m3x2p2x$

Les fractales de Newton
Il est temps de passer aux nombres complexes !

Prenons à présent la fonction f:x->x³-1. Il ne possède qu'une racine réelle (x=1), donc peu importe le choix de x₀ (réel), utiliser la méthode de Newton amènera vers 1.

Mais la méthode de Newton marche également dans le plan complexe, avec des termes initiaux complexes ! Et notre polynôme possède également deux racines complexes : j = -0.5 + i.0.866 et j = -0.5 - i.0.866.
Pour quels x₀ la méthode de Newton nous mènera à x ? Quelles valeurs mènent à j ? Et à j ?

La solution, en image :

Newton2