La sphère cornue

La sphère à cornes, sculpture de Jean-Louis Lhermitte, dans la cour du Centre de mathématiques et d’informatique

Prenez un crayon, une feuille de papier et dessinez-y une courbe revenant à son point de départ sans lever le crayon, ni passer deux fois sur le même point :

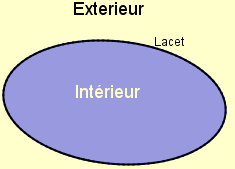
Vous obtenez quelque chose comme ça.

Voilà, vous venez de délimiter le plan en deux parties : l'intérieur et l'extérieur ! Si vous coupiz la feuille le long de la courbe tracée, vous devrez obtenir deux bouts de papiers ! (On appelle ça une "composante connexe"). Jusqu'à là, c'est évident !...

Mais comment le démontrer ? Les adeptes du "ça se voit sur le dessin" (comme Kant) s'en contenteront et passeront à autre chose, les autres (comme Bolzano) déprimeront de ne pas trouver de démonstration. En effet, malgré sa simplicité apparente, la démonstration du théorème de Jordan (Puisque quasi démontré par le français Camille Jordan) est vraiment difficile !

Le théorème de Jordan
Ce que vous venez de dessiner est appelé "courbe de Jordan" (ou lacet simple), c'est-à-dire, une courbe (continue) fermée et simple (sans points double). L'énoncé du théorème de Jordan est le suivant :

Une courbe de Jordan délimite toujours le plan en deux composantes connexes : l'intérieur (qui est borné) et l'extérieur (qui ne l'est pas). Ces deux composantes ont pour frontière la dite courbe.

On peut voir une courbe de Jordan avec l'œil d'un topologue, c'est-à-dire, voir la courbe comme étant un cercle déformé. Notre cercle est un élastique : on peut l'étirer, le plier, mais interdiction de le couper ou de l'écraser. On a même le droit de l'étirer infiniment, du moment qu'on ne le coupe pas.

Lorsque l'on peut passer d'un objet à un autre simplement par déformation, on dit que ces deux objets sont homéomorphes ("de même forme"). Par exemple, un cercle et une ellipse sont homéomorphes (il suffit d'écraser un peu le cercle) ; c'est la même chose entre un beignet (un tore) et une tasse à café (nb : Faire un billet à propos de topologie sans évoquer la ressemblance entre le beignet et la tasse relève d'une faute professionnelle)

Illustration d'un tore-tasse

En fait, la simplicité apparente du théorème vient de notre intuition du lacet simple. On a bêtement tendance à l'imaginer simple... On ne pense pas forcément à des choses comme :

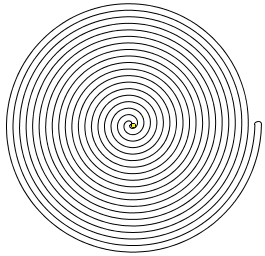
Le point jaune est-il à l'intérieur ou à l'extérieur de la courbe ?
Réponse : à l'extérieur

Le point est-il à l'intérieur ou à l'extérieur de ce flocon de Koch ?
Réponse : On pourrait peut-être le savoir avec une plus grande image...

Bernard Bolzano, au début du XIXe siècle, a été le premier à se dire que ce théorème n'avait rien d'évident. Même s'il a réussi à bien poser la question, il lui a été impossible d'y répondre. Il a fallut attendre la fin du siècle (en 1887), avec Jordan, pour avoir une première version d'une démonstration complète utilisant les prémisses de l'analyse complexe. Entre temps, l'étude des courbes a amené un grand nombre de monstres (Weierstrass et sa courbe continue partout et dérivable nulle part, Peano et sa courbe à deux dimensions...)

La sphère à cornes d'Alexander
Le théorème de Jordan supporte cependant très mal son passage à la dimension supérieure ! Le contre-exemple, c'est la sphère à cornes : cela ressemble à une sphère (pour un topologue), mais ne délimite rien de très simple.

Puisque, en dimension deux, on appelle courbe de Jordan un cercle déformé, on va appeler en dimension 3  "surface de Jordan" (nom inventé pour l'occasion de l'article) une sphère déformée (Un truc qui ressemble à une surface et qui est homéomorphe à une sphère). En toute logique, un extérieur de sphère et un extérieur de surface de Jordan devraient être homéomorphe... Et bien, non ! Cette découverte a été faite au début du XXe siècle par le topologue J. W. Alexander, qui cherchait à généraliser le théorème en 3 dimensions.

Pour cela, il faut construire la sphère à cornes. On va procéder par déformation, pour être sûr de bien avoir affaire avec une surface de Jordan. Pour cela, on part d'une sphère, de laquelle on tire deux cornes que l'on met face à face, sans qu'elles se touchent. Au bout de chacune de ces cornes, on tire deux nouvelles cornes qui s'entrecroiseront (toujours sans se toucher), et on répète l'opération à l'infini. On trouve alors un objet fractale et homéomorphe à une sphère (même s'il est très difficile de le voir au premier coup d'œil) :

La sphère à cornes d'Alexander

On peut alors voir que l'extérieur n'est pas homéomorphe à l'extérieur d'une banale sphère. Pour voir ça, il suffit de remarquer que l'extérieur de la sphère à cornes n'est pas simplement connexe.
Je m'explique. Prenez un élastique vivant, et enfilez-le autour d'un ballon. Cet élastique pourra s'échapper sans problème, aller visiter le reste de l'espace et se contracter autant qu'il le souhaite. On dit alors que l'élastique est homotope à un point. N'importe quel élastique vivant à l'extérieur du ballon peut se contracter, on dit que l'espace est simplement connexe.
Maintenant, imaginons un élastique vivant à l'extérieur d'un tore (d'une bouée). Si celui-ci entoure le tore, il lui sera impossible de se contracter sans déchirer le tore : l'extérieur d'un tore n'est pas simplement connexe (Le tore non plus, d'ailleurs).

Maintenant, on peut imaginer l'élastique vivant autour d'une branche de notre sphère à cornes. Même avec toute la volonté du monde, il n'arrivera jamais à sortir des embranchements, puisqu'ils sont en nombre infinis. L'extérieur de la sphère à cornes n'est pas simplement connexe (et peut plutôt s'apparenter à un tore).
L'un est simplement connexe, l'autre non : ils ne sont pas homéomorphes !

En réalité, la sphère à cornes ne contredit en rien le théorème de Jordan qui reste vrai en n'importe quelle dimension (il y a bien un intérieur et un extérieur, le théorème généralisé s'appelle théorème de Jordan-Brouwer), mais contredit le théorème de Jordan-Schönflies (qui dit que, dans le plan, l'extérieur d'une courbe de Jordan est homéomorphe à l'extérieur d'un cercle)

---

Sources :
Les dossiers de Pour la science n°41 - La sphère à cornes
Beaucoup de wikipédia (Pour toutes les pistes de démonstrations)

Comments

[Robyn Slinger]

Oui c'est vrai, c'est l'homéomorphie des extérieurs qui est en défaut. C'est quand même fascinant.

Bon, allons voir les courbes monstres maintenant !

[El Jj]

A proprement parler, le théorème de Jordan est vrai en toutes dimensions. C'est celui de Jordan-Schönflies (l'extérieur du lacet de Jordan est homéomorphe à l'extérieur du cercle) qui n'est plus vrai en dimension 3, pour une histoire de domaine fondamental. Un élastique autour d'une sphère peut toujours se rétracter en un point, ce qui n'est pas le cas avec la sphère à corne, les deux extérieurs ne sont donc pas les mêmes.
En dimension 2, un lacet tracé autour du disque ne peut se rétracter en un point, et ce, peut importe la "forme" du disque. Cette condition n'est cependant pas suffisante pour montrer que les deux extérieurs sont homéomorphes.

En général, les théorèmes de topologie parlant de domaine fondamental (quels sont les différents types de lacets que l'on peut y tracer) vrai en dimension 2 deviennent faux en dimensions supérieures (un lacet tracé sur un cercle y sera figé, alors que sur une sphère, il pourra toujours se rétracter).

[Robyn Slinger]

J'imagine que si le théorème de Jordan avait dû être vrai en dimensions supérieures il aurait été plus simple à démontrer en dimension 2*.

Par contre, j'essaye de comprendre ce qui s'oppose à la construction d'un "cercle à cornes d'Alexander" pour la dimension 2, mais je ne vois pas. Je veux dire, je le "vois" bien (en essayant d'imaginer un cercle en caoutchouc), mais je n'arrive pas à mettre le doigt sur la raison essentielle qui fait qu'avec le cercle ça ne marche pas alors qu'avec la sphère oui.

--

* Même s'il y a des exemples célèbres contredisant cet argument. Par exemple le théorème de la dimension, qui dit que des ouverts de R^n et R^m ne peuvent être homéomorphes que si n = m -- c'est très facile si n ou m = 1 (et peut-être 2), mais nettement moins dans les autres cas.