Sám u sebe v hlavě magického pí číslic deset mám
Même s'il ne donne pas vraiment l'heure exacte, le porte-crayon-thermomètre-horloge de mon bureau est très clair : aujourd'hui, nous sommes le 3/14, ce qui fait de ce jour un jour exceptionnel : le Pi Day ! Le principe de cette journée est très simple : il faut célébrer le nombre pi ! On peut par exemple se raconter des anecdotes sur notre relation avec pi, réfléchir à ce que serait le monde sans pi, bâtir les fondations d'un temple au dieu Pi...
Gros soucis : j'ai déjà sur ce blog abordé beaucoup de sujets autour du nombre pi : l'histoire du calcul de ses décimales, ses propriétés (pi est irrationnel, transcendant et probablement univers, équiréparti et normal), l'algorithme compte-gouttes, la formule BBP, ce que serait le monde si on ne s'était pas trompé dans la définition de pi... Comme il restait encore plein de trucs que je ne savais pas trop où placer, voici, pour célébrer le Pi Day, le top 10 des choses anecdotiques impliquant le nombre pi !
N°3 : Le Pi Day

Le barbu de la photo est le mec qui a inventé cette fête...
Tiens, justement, c'est aujourd'hui : la date du 14 mars, écrite en anglais, donne 3-14, les premières décimales de pi ! C'est donc le jour où l'on fête ce nombre. Le point culminant de la fête se doit d'être à 1h59, pour fêter en plus la minute annuelle de pi.
Les origines de la fête remontent à 1989, sous l'idée du physicien Larry Shaw. Le public était alors invité à l'Explatorium, un musée de San Francisco, pour y manger des tartes (pour faire un fin jeu de mots en anglais).
On fête donc aujourd'hui le 22e anniversaire de la fête. On retiendra aussi son 15e anniversaire, quand David Tammet (l'autiste qu'on voit souvent à la télé) a récité 22514 décimales de pi. Pour son 20eme anniversaire, le gouvernement américain a même approuvé une résolution faisant du 14 mars la journée nationale de Pi. Le meilleur anniversaire du Pi day reste quand même le -110e, qui a vu la naissance de Albert Einstein.
Quelques variantes de la fête existent, mais n'ont guère trouvé un succès comparable, notemment :
- le 22 juillet (22/7 au format français), où l'on fête la journée de pi approximative, puisque 22/7 est une approximation classique de pi.
- le 10 novembre, qui est le 314e jour de l'année
- le 23 octobre à 6h02, où les chimistes fêtent la mole (en référence au nombre d'Avogadro, qui vaut 6,02×1023.
N°1 : Pi en base 26
d,drsqlolyrtrodnlhnqtgkudqgtuirxneq
bckbszivqqvgdmelmuexroiqiyalvuzvebm
ijpqqxlkplrncfwjpbymggohjmmqismssci
On connait souvent pi écrit en base 10 (3.1416...), mais qu'en est-il en base 26 ? En remplaçant chaque chiffre par la lettre qui correspond dans l'alphabet (en remplace 0 par A, 1 par B, 2 par C...), on trouve une série de lettres plus ou moins aléatoire dans lequel on ne peut s'empêcher de chercher un certain sens. Le premier mot français qui apparaît est donc le mot "tu", suivi de "ne", puis "me" et "mue". On remarque aussi que les décimales se moquent ouvertement de nous, en proposant "lol" après seulement 5 décimales, et en écrivant presque bien "rond". En persévérant dans la lecture, on trouve le mot "rêve" et le mot "sexué" (à la 1645e position). Côté mots anglais, on peut trouver "oxygen" (11582e position), "subplot" (115042e position) et "armagnac" (305146e position). Aucun mot (anglais) de plus de 8 lettres n'a été découvert dans les 7 premiers millions de décimales de pi.
On peut aussi écrire Pi en base 27, en transformant 1 en A, 2 en B etc. Un site propose de faire la recherche des mots que l'on préfère dans ces 27-cimales. Toute sortes de statistiques y sont décrites, on peut notemment apprendre que le premier personnage du Seigneur des Anneaux qui apparaît dans les décimales est... Sam !
N°4 : Le mystère de exp(π.√163)
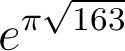
Prenons le nombre pi, l'exponentielle, la racine carrée et le nombre premier 163, et mélangeons le tout. En mélangeant tout ça, on devrait a priori obtenir un nombre complètement banal... Et pourtant, quand on effectue le calcul, on tombe sur
eπ.√163 = 262537412640768743, 9999999999992...
Ce nombre, parfaitement irrationnel, est presque un entier ! A 10-12 près, c'est quand même pas mal (si on avait voulu le faire exprès, on aurait pas réussi). La découverte de ce phénomène est attribuée à Alexandre Aitken, et on est aujourd'hui incapable d'expliquer d'où ça vient ! En changeant 163 par d'autres nombres entiers, on trouve relativement souvent des nombres presque entiers, ce qui prête à penser qu'il y a là un authentique mystère à étudier.
Quelques éléments de réponse tout de même : s'il y a bien un mystère, il sera difficile à étudier ! On peut voir qu'elle a des liens avec la fonction modulaire j (celle du monstrous moonshine)... Avec cette observation, on a pu fabriquer de très jolis nombres presque entiers, comme :
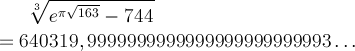
N°1 : Le programme de Lievaart

Ceci est un programme écrit dans le langage C où toutes les variables ressemblent plus ou moins à pi. Et ce programme permet évidemment de calculer la suite des décimales de... e !
N°5 : Le mystère des séries de Leibniz
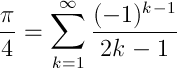
La série de Leibniz, et on le sait depuis Leibniz, est une série infinie qui converge vers π/4. La série est infinie, mais si on ne prend qu'un nombre fini de termes, on peut théoriquement obtenir une approximation de pi. Dans la pratique, on n'utilise jamais cette série pour approximer pi, la convergence est bien trop mauvaise (après n termes, l'erreur est de l'ordre de 1/n). Ainsi, si on fait la somme en prenant les 50 000 premiers termes, on obtient seulement 4 décimales correctes :
3.1415726535897952384626423832795041041971666293751
La valeur exacte de pi étant :
3.1415926535897932384626433832795028841971693993751
Fait particulièrement étrange : les premières décimales de la valeur approchée de pi sont toutes correctes, à quelques décimales près ! Pourquoi cette étrangeté ? Personne ne le sait !
En fait, si, on le sait. Le phénomène, observé pour la première fois en 1982, s'explique grâce aux formules d'Euler-Mc Laurin. Dans les bons cas (N multiple de 4), on a le développement asymptotique suivant :

Autrement dit, quand N est une grande puissance de 10, les décimales fausses de développement décimal seront isolées. Notons au passage que le phénomène est moins présent quand on prend les 50001 premières décimales :
3.1416126531897992384226427832755041441967666333751
N°9 : Le point de Feynman
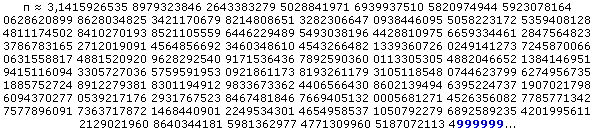
Le point de Feynman est la 762e décimales de pi : c'est à partir de ce point que toutes les décimales de pi sont des "9" ! C'est lors d'une conférence que le physicien Richard Feynman a expliqué qu'il aimerait apprendre les décimales de pi jusqu'à la 767e pour le plaisir de dire "neuf neuf neuf neuf neuf neuf et caetera".
C'est tout de même étonnant de trouver une suite de 6 chiffres identiques si tôt dans la suite des décimales. On se rassure en se disant que la première occurence de 9999999 dans la suite des décimales n'intervient qu'à la 1722776e décimale.
N°2 : Le poème de Michael Keith

Circle digits : a self referential story, par Michael Keith (402 décimales)
Pour se souvenir des décimales de pi, on peut essayer d'apprendre le poème suivant
- Que j'aime à faire apprendre un nombre utile aux sages !
- Immortel Archimède, artiste ingénieur,
- Qui de ton jugement peut priser la valeur ?
- Pour moi, ton problème eut de pareils avantages.
En comptant le nombre de lettres de chaque mot, on retrouve la suite des décimales de pi, les mots de 10 lettres comptant comme un "0". Dans son intégralité, le poème permet de se rappeller les 126 premières décimales.
En modifiant un peu les conventions (les ponctuations (excepté le point) comptent comme des zéros, les mots de plus de 10 lettres comptent comme deux chiffres...), Michael Keith a proposé un texte autoréférentiel permettant de connaître les 402 premières décimales de pi. Il réitère en 1995 avec les mêmes contraintes, et écrit un poème donnant 740 décimales, un record.
N°6 : 133 caractères pour 15000 décimales
![]()
Ce programme, codé en C, est le record du plus petit programme permettant de calculer les décimales de pi. En seulement 133 caractères, ce programme permet de calculer, via l'algorithme goutte à goutte, les 15000 premières décimales de pi.
N°5 : Le projet de loi Pi de l'Indiana
Durant l'année 1897, le mathématicien amateur Edward Goodwin proposa à la Chambre des Lois de l'Indiana un texte de loi fixant une bonne fois pour toutes des formules permettant d'effectuer différents calculs d'aires, ou d'effectuer la quadrature du cercle. En filigrane, cette loi allait fixer à pi les valeurs de 4, 3.1604, 3.2 ou 3.232. (et prévoyait également que √2 = 10/7). Le texte ne fut heureusement pas adopté, les législateurs jugeant finalement qu'aucun texte de loi ne pouvait fixer des vérités mathématiques... Goodwin n'était pas n'importe qui : il avait auparavant résolu les 3 grands problèmes de l'antiquité (démontrés insolubles quelques temps plus tôt) et fait paraître ses découvertes dans les premiers numéros de l'American Mathematical Monthly (qui, depuis, est devenu une revue respectable et respectée).
N°3 : Coïncidence numérique

Si on calcule la somme infinie ci-dessus, on trouve que ses décimales correspondent à celles de pi. Quand on étudie de plus près cette somme, on découvre qu'elle n'est pas égale à pi (preuve donnée par les frères Borwein en 1992). Mais quand on calcule un peu plus, on s'aperçoit que les décimales de pi et celles de la série infinie coïncident sur... 42 milliards de décimales ! Au delà, elles n'ont plus rien en commun...
C'est le plus bel exemple de coïncidence numérique, qui nous rappelle qu'une preuve ne remplacera jamais un calcul approximatif !...
Sources :
Le fascinant nombre pi ; Jean-Paul Delahaye
A la poursuite de pi ; Jörg Arndt, Christoph Haenel
Pour l'image : là



/http%3A%2F%2Fstorage.canalblog.com%2F06%2F96%2F210892%2F102825337_o.jpeg)
/http%3A%2F%2Fstorage.canalblog.com%2F85%2F70%2F210892%2F65561362_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F30%2F49%2F210892%2F60870097_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F67%2F67%2F210892%2F13600311_o.png)