La topo, c'est rigolo II : La bouteille de Klein

"Dans l'enfer topologique, la bière est contenue dans des bouteilles de Klein" [Bonne blague disponible gratuitement sur internet]

Après l'anneau de Moëbius, passons à une curiosité topologique de haute importance (relative) qu'il faut absolument connaître pour pouvoir se montrer intelligent dans un dîner mondain de mathématiciens : la bouteille de Klein.

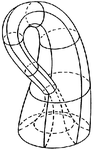
Tout d'abord, voici l'objet en photo (enfin, en dessin):

Une bouteille de Klein véritable.

Cette surface est bien jolie, mais quelle est donc son intérêt ? Et bien tout comme l'anneau de Moebius , la bouteille de Klein n'a qu'une seule face (j'ai pas de fourmis pour le prouver, par contre. Et, encore plus fort, elle n'a aucun bord !

Prolongeons un peu notre culture générale sur la bouteille, avec une deuxième grande question : "Pourquoi qu'on appelle ça... hips... une bouteille, alors qu'il n'y a... hips... même pas de bière dedans ?"
Et bien, parce que le traducteur allemand a quelque peu cafouillé, en traduisant kleinsche Fläche par Bouteille de Klein (Alors que les plus germanophones des lecteurs auront bien traduit Surface de Klein (Eh oui, bouteille, ça se dit Flasche))

Il est maintenant tant de rétablir la vérité, toutes les bouteilles de Klein ne ressemble pas à ça :

(Je parle de la bouteille en verre, pas du mec)

Mais peuvent ressembler à ça :

En fait, une bouteille de Klein, c'est juste un surface sans bord qui n'a pas d'intérieur...
Vous l'avez surement remarqué, chaque figure a toujours une auto-intersection. Dessinés, ils sont moins jolis, mais pour éviter une autointersection, il faudrait les faire en 4 dimensions (ce qui, en soit, n'est pas évident)...

- Monsieur, monsieur, je veux faireune bouteille de Klein en papier !

S'il vous plaît, arrêtez de m'interrompre dans mes exposés, j'y venais justement...
Donc, comment faire ? Et bien, il suffit de coudre deux anneaux de Moëbius le long de leur côté... (En fait, c'est impossible à faire, mais vous pouvez toujours tenter)

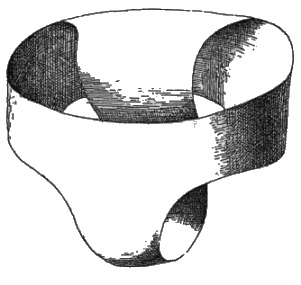
Dernière chose très importante : qu'obtient t'on lorsque l'on perce une bouteille de Klein ?
...
...
Et bien, ou obtient un slip de Moëbius !

Ceci était le deuxième communiqué du mouvement de mathématiciens Devenez topologistes.

---

Sources :
Plein de choses ici
La bouteille de Klein en verre

Comments

[Tût-tûûût]

Pour les gens qui échoueraient à Paris un de ces quat' matins et qui aiment bien les trucs scientifiques, allez vous perdre au palais de la découverte. Au programme, des bouteilles de Klein en 3D et autres petites choses topologiques. Par contre, on peut pas essayer de les remplir... Dommage.

Sinon j'adore le slip de Moebius :D

[titefrog]

looool!!

mais ça sert à quoi une bouteille de klein alors... si on ne peut rien mettre dedans ni en sortir son contenu si elle en a ... peut être juste à faire beau...

[Pierre]

Vu qu'on ne peut rien mettre dans la bouteille du Petit, la couche culotte dure plus longtemps alors...

[procrastin]

haha, fantastique le slip de Moëbius. Il dure deux fois plus longtemps puisqu'on peut le porter une fois à l'endroit te une fois à l'envers, si tant est que l'endroit et l'envers ait un sens le concernant...

[Phoenixx]

"Devenez topologistes" qu'il disait ... Enfin si on peut pas la remplir ta bouteille, je vois pas l'intérêt XD