Au-dessus de la moyenne

"Un grand patron français gagne en moyenne 300 smics", "La durée de vie moyenne d'une faille est de 348 jours", "j'ai déjà vu des threads où la taille moyenne allait autour des 20", "J'ai eu mon semestre avec 16 de moyenne" ou "C'est quoi la vitesse moyenne des coureurs du Tour de France ?" ...
Le mot "moyenne", tout le monde l'emploie, et d'ailleurs, tout le monde sait globalement à quoi cela correspond : une valeur représentative de tout un ensemble de données. Une sorte de milieu, en fait.

Pour la calculer, ça aussi, n'importe quel allergique aux maths peut le faire, parce que ça sert toujours en cours de français pour savoir quelle note il va falloir au prochain contrôle pour rattraper ce 03/20 dans un contrôle sur les probabilités.
Cette moyenne, c'est la moyenne arithmétique. On additionne toutes les valeurs et on divise par leur nombre.

La moyenne harmonique...
Et la vitesse moyenne du coureur cycliste ? Celui qui fait du 20km/h sur 1km en montée et du 80 km/h sur une descente de 1 km ?
Je vous laisse réfléchir.............
(20+80)/2=50. Il aurait donc une moyenne de 50 km/h ?...
Si je pose la question, c'est évidemment parce que cette réponse est fausse. Il aurait plutôt fallu répondre 32km/h, puisque notre ami le coureur va passer beaucoup plus de temps sur la montée que sur la descente (Je ne fais pas le détail des calculs ici).
Avec nos données, on a eu trop vite tendance à calculer la moyenne arithmétique, alors que c'est la moyenne harmonique qu'il fallait utiliser. (On divise le nombre de valeurs par la somme des inverses des données)


La moyenne géométrique...
Autre situation, autre problème.
Le 7 mars 2006, 400 000 personnes (selon la police) ou 1 000 000 (selon la CGT) manifestent à travers la France contre le CPE.
Quels chiffres croire ? La police a plutôt tendance à amoindrir le nombre, et les organisateurs ont tendance à le grossir, en plus de l'imprécision du compte.
Faire une moyenne arithmétique (700 000 personnes), ça donne un très net avantage à la CGT ; en imaginant que la police donne 10 fois moins de manifestants (-90%), la moyenne arithmétique atteindrait 520 000 personnes (-26%). Le chiffre de la CGT écrase celui de la police.
Imaginons plutôt que la police et la CGT fonctionnent de la même manière : d'un côte, la police sous-compte (par exemple, pour 4 manifestants, 3 seront comptés, soit -25%) et de l'autre côté, la CGT sur-compte (pour 4 manifestants, 5 seront comptés, soit +25%). Les deux utilisant les même coefficients. C'est là que la moyenne géométrique intervient ! Il suffit de calculer la racine carrée du produit des deux valeurs.
Dans notre cas, on peut estimer le nombre de manifestants du 7 mars 2006 à 632 500 (La CGT risque de faire la gueule...)

Les autres
Il existe d'autre types de moyenne qui ont leur utilité en mathématiques, comme la moyenne quadratique, la moyenne arithmético-géométrique, la moyenne glissante...

Et histoire de finir joliment cette note, pour tous les gens venant de google cherchant des informations sur les moyennes, voici une petite liste récapitulative :

Moyenne arithmétique :


Moyenne harmonique :


Moyenne géométrique :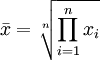



Moyenne quadratique :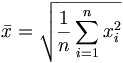


Et pour finir en beauté, le cas général :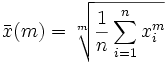

• pour m = 1, on a la moyenne arithmétique
• pour m = 2, on a la moyenne quadratique
• pour m = -1, on a la moyenne harmonique
• pour m tendant vers 0, on a la moyenne géométrique
• pour m tendant vers l'infini, on a la plus grande valeur de la série.

---

Sources :
BibMath et Wikipédia

Comments

[asmae]

s'il vous plait j'ai un probléme dans la distinction entre les moyennes harmonique,géométrique et quadratique.

[Bertie]

Effectivement D0m3 à raison si on prend la logique qui est mise en oeuvre dans cet article.

Cas 1: les "compteurs" sont de mauvaise foi (les deux)
La police compte 4 et la CGT compte 4 aussi, puis la police décide de baisser les chiffres en faisant -25% et la CGT de les gonfler en faisant +25% : à ce moment là la moyenne arithmétique est exacte (à condition que le pourcentage d'augmentation ou baisse soit le même à la CGT et dans la police).

Cas 2: les "compteurs" sont de bonne foi
Donc la police compte effectivement 3, et la CGT compte effectivment 5. Les différences sont dues aux biais méthodologiques employés par les parties. Si on cherche à corriger ces biais, cest à dire trouver le résultat tel que (le résultat de la police) + X% soit égal au (résultat de la CGT) - X%, alors on a besoin de la moyenne géométrique : ils sont tous de bonne foi et se trompent "dans les mêmes proportions".

Cas 3: Un peu du cas 1 et un peu du cas 2 => on ne peut rien conclure!!!

A vous de vous faire votre avis...

En tout cas on voit l'intérêt d'un calcul indépendant. Par contre pour faire le calcul, il faut des gens présents à la manif qui comptent, donc hors police et syndicats, c'est difficile à faire. Une commission ne fera pas grand chose de + que de se prononcer en fonction des résultats remontés du terrain, si elle n'a pas de personnel.

[D0m3]

Imaginons plutôt que la police et la CGT fonctionnent de la même manière : d'un côte, la police sous-compte (par exemple, pour 4 manifestants, 3 seront comptés, soit -25%) et de l'autre côté, la CGT sur-compte (pour 4 manifestants, 5 seront comptés, soit +25%). Les deux utilisant les même coefficients.

Dans ce cas la moyenne arithmétique tombe juste alors que la moyenne géométrique est fausse.
4 manifestants, la police annonce 3, la CGT annonce 5. Moyenne arithmétique 8/2 = 4, moyenne géométrique sqrt(3*5) = 3.87.

Quel intérêt ? La moyenne géométrique est une meilleure estimation dans le cas où les valeurs les plus élevées sont les plus éloignées de la vérité.

Ainsi si la CGT compte 6 manifestants pour 4, la moyenne arithmétique est 4.5, et la géométrique est 4.2.

En bref, dans votre article, vous sous-entendez que la CGT gonfle plus les chiffres que la police ne les diminue. Il faudrait donc le dire de manière explicite, car c'est totalement faux si la police sous-estime plus le nombre de manifestants que la CGT ne le sur-estime.

[haz]

montrer que si a,betc sont trois termes consécutifs d'une suite arithmétique, alors b=a+c/2

[Enro]

David > Super, merci !