Extraits de naissance des entiers naturels

"Dieu fit les nombres naturels ; tout autre est l'œuvre de l'homme" [Leopold Kronecker]

Par pure provocation iconoclaste, j'affirme plutôt qu'en mathématiques, Dieu a créé rien, et que les entiers naturels (0, 1, 2, 3, 4, ...) sont l'œuvre de l'homme !

Pour commencer ma grande saga des nombres (qui j'espère me fournira des sujets pour un grand nombre d'articles à venir), commençons par le commencement, avec les nombres entiers naturels, amoureusement notés ℕ, et les différentes façon de les fabriquer à partir de rien.

Les entiers naturels selon Gottlob Frege (1884)
Prenons au hasard un troupeau de narvals, un troupeau de nautiles, un troupeau de nandous, un troupeau de noctuelles et un troupeau de najas.

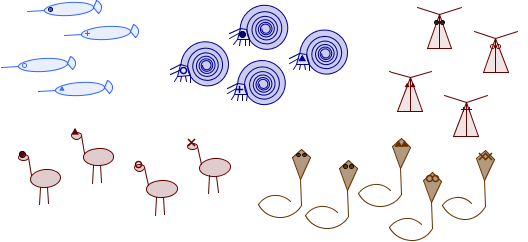
Troupeaux de narvals, de nautiles, de noctuelles, de nandous et de najas

Le programme de mathématiques de maternelle met l'accent sur la nécessité de l'abstraction, afin de faire émerger le concept de nombre en faisant le passage au quotient sur une relation d'équivalence, celle de l'équipotence.
Dans la pratique, cela consiste à remarquer qu'il y a autant de narvals que de nautiles, mais pas autant que de najas...

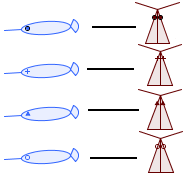
Prenons les troupeaux de narvals et de noctuelles, puis mettons-les en rang, deux par deux. Chaque narval a sa noctuelle, chaque noctuelle a son narval, aucun n'est délaissé. Nous venons de faire une correspondance biunivoque entre les narvals et les noctuelles : ces deux troupeaux sont donc "équinumériques" ou "équipotents" (ils possèdent "autant" d'éléments). On pourrait faire la même chose avec les nandous ou les nautiles : tous ces ensembles sont équipotents. Indépendamment du fait qu'il s'agisse d'animaux grossièrement dessinés, ces troupeaux ont pour point commun de posséder "autant" d'éléments. Ces troupeaux forment une classe d'équivalence, celle des ensembles possédant autant d'élément qu'il y a de narvals dans mon troupeau. Par commodité, on appellera "4" cette classe d'équivalence !

Par contre, impossible d'accoupler les narvals avec les najas, l'un de ces dernier sera forcément délaissé. Il n'y a donc pas autant de narvals que de najas. Par contre, puisque je peux les appareiller avec les doigts de ma main droite, il y a équipotence entre mes doigts droits et le troupeau de najas.  Les najas et les doigts forment une classe d'équivalence différente, notée "5".

Pour le logicien allemand Frege, les nombres naturels, c'est ce qui permet de différencier les ensembles finis d'objets. Le monde des collections finies d'objets est donc divisé en ℵ₀ catégories : les collections qui possèdent 4 objets, les collections qui possèdent 5 objets, les collections qui possèdent 42 objets, les collections qui possèdent 0 objet...

En mettant un peu d'ordre à tout ça, on trouve que les entiers naturels sont :
0, 1, 2, 3, 4, ...

On appelle cet ensemble ℕ, et cela suffit dans la vie quotidienne pour compter le nombre de patates nécessaire pour faire des frites pour 4 personnes.

Les entiers naturels selon Peano (1889)
En son temps, Euclide a définit les axiomes de la géométrie, ie, les vérités premières à partir desquelles découle toute la géométrie. 2200 ans plus tard, le mathématicien italien Giuseppe Peano s'est penché sur le cas des nombres entiers. Après un long brainstorming avec Dedekind, il a proposé un ensemble de 5 axiomes, définissant l'ensemble des entiers naturels de façon récurrente. Ils ont ainsi créé un ℕ idéal, indépendant de la réalité, contrairement à Frege. Heureusement, ils ont bien bossé, et les deux définitions se correspondent bien !

Les axiomes de Peano sont les 5 axiomes suivant :
(0) - 0 est un entier naturel
(1) - Tout entier n admet un successeur, noté "S(n)", ou "succ(n)", ou "n+1"
(2) - Aucun entier n'admet 0 pour successeur
(3) - Deux entiers qui possèdent le même successeur sont égaux
(4) - Si un ensemble contient 0 et le successeur de tous ses éléments, alors cet ensemble est celui des entiers naturels.

De nulle part sort le nombre 0 (par l'axiome 0), qui engendre à lui tout seul tous les autres entiers (par l'axiome 1). Les 3 autres permettent de donner une contenance aux nombres créés par les deux premiers axiomes.

Pour Peano, les entiers naturels sont donc :
0 - 0
1 - S(0) (ie "l'entier qui suit 0")
2 - S(S(0)) (ie "l'entier qui suit l'entier qui suit 0")
3 - S(S(S(0)))
4 - S(S(S(S(0)))), ...

Pour plus de commodité, on les renomme en 0, 1, 2, 3, 4, ... En ajoutant les bonnes définitions de la somme, de la multiplication et de toutes ces choses là, on récupère ce que l'on connaissait déjà intuitivement : l'arithmétique !
Les axiomes de Peano sont la base de l'arithmétique, et suffisent pour répondre aux principales questions du genre "Quel nombre suit 19 551" ou "existe-t-il une infinité de nombre premier ?".

Les entiers naturels selon Von Neumann (194?)
Le problème des nombres entiers selon Peano, c'est que non seulement, ils sortent de nulle part, mais surtout qu'ils ajoutent 5 axiomes. Avec les 8 axiomes de la théorie des ensembles (ZFC), c'est 5 axiomes de trop ! L'idéal, ça serait de construire les entiers naturels dans la théorie des ensembles, ce qui rendrait superflus les 5 axiomes.

Pour construire les nombres entiers naturels dans la théorie des ensembles, "il suffit" d'y trouver un ensemble qui correspond aux axiomes de Peano. Autrement dit - sautez au paragraphe suivant si vous n'avez pas validé une L1 de maths - , il faut trouver un triplet (N,z,S) où N est un ensemble (l'ensemble des nombres entiers), z∈N (le zéro de l'ensemble) et S:N→N (l'application "nombre suivant") qui vérifient :
(2) - z ∉ S(N)
(3) - S est injective
(4) - Si un ensemble F vérifie z∈F et S(F)⊂F, alors F=N
Un tel triplet est appelé structure de Dedekind-Peano.

Grâce à l'intervention divine du début de l'article, il existe rien. Rien, c'est l'ensemble vide, noté ∅. Puisque l'on a que ça, on va le garder pour faire office de 0. Après, il faut choisir l'opération successeur :

* En prenant S(n)={n}, les entiers naturels seront :
0 = ∅
1 = {0} = {∅}
2 = {1} = {{∅}}
3 = {2} = {{{∅}}}
L'ensemble N = {0,1,2,3,...} représente parfaitement l'ensemble des entiers naturels.

* En choisissant S(n) = n ∪ {n}, on obtient la construction de Von Neumann :
0 = {} = ∅
1 = {0} = {∅}
2 = {0,1} = {∅,{∅}}
3 = {0,1,2} = {∅,{∅},{∅,{∅}}}
4 = {0,1,2,3} = {∅,{∅},{∅,{∅}},{∅,{∅},{∅,{∅}}}}

Hormis celui d'offrir une écriture horrible, l'intérêt essentiel de la construction de Von Neumann est de pouvoir dire aussi bien a≺b si et seulement si a ∈ b.

* En choisissant 0={∅} et S(n) = {n ∪ {{n}}}, on aura une autre construction des entiers naturels, dite construction Jjienne des entiers naturels :
0 = {∅}
1 = {{∅,{{∅}}}}
2 = {{{∅,{{∅}}},{{{∅,{{∅}}}}}}}
3 = {{{{∅,{{∅}}},{{{∅,{{∅}}}}}},{{{{∅,{{∅}}},{{{∅,{{∅}}}}}}}}}}

Cette construction n'a absolument aucun intérêt, sinon celui d'être encore plus difficile à écrire que la construction de Neumann (mais l'effet de surprise est passé de 60 ans...)...

En fait, peu importe le choix du zéro et celui de l'opération successeur (tant qu'elle vérifie les propriétés de Dedekind-Peano), on obtient toujours la même chose (un truc qui ressemble à {0,1,2,3,...}), au détail de l'écriture près.

Le fait d'inscrire les entiers naturels (et donc l'arithmétique) dans un cadre plus grand permet de répondre à des questions sur les nombres qui la dépasse, comme le théorème de Goodstein, ou toutes les questions sur la répartition des nombres premiers.

Les entiers naturels selon Church (1930)
Peano voit tout en entiers, Zermelo et Fraenkel (les fondateurs de l'axiomatique de la théorie des ensembles) voient tout en ensembles. De son côté, Church voit tout en fonctions, en fondant la théorie du lambda-calcul (un grand pan de l'informatique théorique).

Au final (et après tout un tas de considérations vulgarisée là-bas), le logicien Barendregt simule les entiers  naturels sous la forme :

0 = (λn.n)(λxy.x)
1 = (λxyz.zxy)(λxy.y) 0 = (λxyz.zxy)(λxy.y)(λn.n)(λxy.x)
2 = (λxyz.zxy)(λxy.y) 1 = (λxyz.zxy)(λxy.y)(λxyz.zxy)(λxy.y)(λn.n)(λxy.x)
etc.

Ce dernier paragraphe, c'était juste par plaisir d'écrire des longues formules en lambda calcul... Dans la réalité, les spécialistes de lambda calcul n'écriront jamais de telles atrocités !

---

Sources :
Wikipedia sait plein de choses sur les axiomes de Peano et sur les entiers naturels.

---

Autres articles de cette série : ℕ,  ℤ, ℚ, ℝ, ℚ_p, ℂ (1), ℂ (2), H, 𝕆, ℚ(α), 𝔽_q, No

Comments

[Villette]

Il y a aussi les nombres suréel de Conway qui donnent naissance aux nombres naturels (entre autre). Sinon article très intéressant!

[orpheu48]

Bonjour,
je ne suis pas mathématicien ni prof, mais je me suis intéressé aux fondements des maths.
Von Neumann a ajouté un axiome selon lequel un ensemble ne peut pas être ELEMENT de lui-même. (je ne confonds pas ELEMENT et PARTIE). Donc cet axiome n'existait pas dans la théorie antérieure. Dans une théorie sans cet axiome, pourrais-je avoir un ou quelques exemples d'ensemble se contenant lui-même(ou s'appartenant à lui-même,ce qui, ici seulement, revient au même) comme élément? Et par exemple qu'en est-il chez Frege et la constitution de la suite des entiers naturels?
Je peux vivre sans la réponse, mais ça me taquine...
Merci beaucoup à qui m'éclairera.

[dcodeur]

Quid du débat à propos du fait que l'ensemble des entiers naturels commencent par 1 ?

J'attends l'article sur l'ensemble des nombres relatifs la semaine prochaine sur mon bureau :D