Il y aurait une infinité de nombres premiers...

C'est dans l'ordre des choses : quand un mathématicien démontre un théorème tellement génial qu'il en devient évident, tous ceux qui suivent ne peuvent s'empêcher d'y ajouter leur grain de sel, en proposant leur propre démonstration du fait en question.

De Euclide au 20e président des USA, tout le monde s'est penché sur le théorème de Pythagore (79 recensées là-bas). J'avais aussi donné à l'époque 4 démonstrations de la divergence de la série harmonique... Mais c'est surement la loi de réciprocité quadratique qui possède le record : plus de 233 preuves à travers l'Histoire (Legendre, Gauss, Jacobi, Lebesgue et tellement d'autres...)

Tous les grands théorèmes possèdent d'innombrables démonstrations, chacun ayant leur propres qualités. Pour le théorème de Pythagore, par exemple, on peut préférer les démonstrations élémentaires de géométrie (élémentaires dans le sens où elles ne font pas intervenir de concepts éloignés au problème initial), on peut préférer la démonstration en une demi-ligne, mais il faut d'abord assimiler le concept de produit scalaire et d'espace Eucliden. On peut même apprécier les démonstrations qui sortent de nulle part, comme  la démonstration physique faisant appel à l'hydrostatique (voir Pour la science n°388), ou cette non-démonstration avec de l'eau.

Un autre théorème qui a fait couler beaucoup d'encre est celui qui annonce "il existe une infinité de nombres premiers". Aujourd'hui, découvrons au 11 bonnes raisons indiquant qu'il existe un nombre infini de nombres premiers (même si, évidemment, une seule d'entre elles suffirait).

Démonstration d'Euclide (-300)
Cette démonstration étant la plus connues de toutes, j'en avais déjà parlé là-bas, avec sa réécriture en 33 mots, sans E ou en haïku. Je vous y renvoie

Supposons qu'il existe un nombre fini de nombres premiers p₁, p₂, ..., p_r. Posons alors P=p₁....p_r+1.
Soit p un nombre premier divisant P. Si ce nombre fait partie de la liste p₁, ..., p_r, alors il diviserait P-p₁....p_r=1, ce qui est absurde.
Il existe donc un nombre infini de nombres premiers.

Notons tout de même qu'il n'y a aucune raison que le nombre 2×3×5×...×p_r+1 (noté pr#+1) soit premier ; la démonstration d'Euclide met juste n évidence que les facteurs premiers de pr#+1 sont tous plus grands que pr. (Par exemple, 13#+1=30031 n'est pas premier... Le plus grand nombre premier connu de cette forme est le nombre 392 113#+1, qui possède 169 699 chiffres)

Démonstration de Kummer (1978)
Une alternative à la démonstration d'Euclide, mais qui reprend en fait les mêmes idées

Supposons qu'il existe un nombre fini de nombres premiers p₁, p₂, ..., p_r. Posons alors N=p₁....p_r (>2)
Soit p un facteur premier de N-1. p divise N et divise N-1, donc divise N-(N-1)=1. C'est absurde !
Il existe donc un nombre infini de nombres premiers.

Démonstration de Goldbach (1730)
On peut aussi démontrer qu'il existe une infinité de nombres premiers sans faire appel à la démonstration par l'absurde, en exhibant une suite infinie de nombres premiers distincts. Ça, on ne sait malheureusement pas bien faire... On peut s'en sortir en exhibant une suite a₁, a₂, ... infinie de nombres deux à deux premiers entre eux (deux nombres de cette suite n'auront jamais de facteurs premiers en commun). En prenant pour chaque a_i un facteur premier, on trouvera une suite infinie de nombres premiers distincts.
Cette démonstration, que j'attribue ici à Goldbach (d'après là), semble aussi être attribuée à Polya et Szego (1924), d'après un exercice de Hurwitz (1891)... (d'après [Rib])

Considérons la suite des nombres de Fermat : F_n=2^{2^n}+1 (F₀=3, F₁=5, F₂=17, F₃=257, ...). Notons que les nombres de Fermat sont impairs. On peut vérifier par récurrence que, pour m>0, F_m-2=F₀.F₁....F_m-1.
Si n<m,>

_n divise F_m-2. Si p est un facteur commun à

F_n et à F_m, alors il est aussi commun à F_m-2, et donc, p diviserait F_m-2-F_m=2. Donc p=2, ce qui est absurde (puisque les nombres de Fermat sont impairs).
Les nombres de Fermat sont donc premiers entre eux deux à deux, ce qui prouve qu'il existe une infinité de nombres premiers.

D'autres suites donne des nombres premiers entre eux deux à deux :

Les suites de Lucas (≈1870) : (Je donne pas ici la démo) Pour S₀ impair, on définit la suite (S_n) par récurrence : S_n=S_n-1²-2. Cette suite, qui ne donne que des nombres premiers entre eux, se retrouve notamment dans le test de Lucas-Lehmer, qui permet de découvrir les plus grands nombres premiers connus aujourd'hui.

Les suites de Edwards (1964) : (Je donne pas de démo ici non plus) Soit S₀ et a deux nombres premiers entre eux (avec 1≤a < S₀). La suite définie (S_n) par récurrence S_n=S_n-1(S_n-1-a)+a donne une suite de nombres premiers entre eux deux à deux (pour a=2 et S₀=3, on retrouve la suite des nombres de Fermat...)

Les suites de Bellman (1947). (Je donne pas plus de démo ici) Considérons un polynôme f(X)=a_nXⁿ+...+a₀ tel que a₀≠0 et, si n et a₀ sont premiers entre eux, alors f(n) et a₀ sont premiers entre eux.
En disposant d'un tel polynôme, on peut fabriquer la suite de polynôme f_m(X) par récurrence, en posant f₁(X)=f(X), et f_m+1(X)=f_m(f(X)).
Si n et a₀ sont premiers entre eux, alors la suite f₁(n), f₂(n), f₃(n)... donne une suite de nombres premiers entre eux.
En prenant notamment f(X)=(X-1)²+1 et n=-1, on retrouve la suite... de Fermat !

Variante de Schorn (????) : En prenant un entier n≥1 quelconque, les nombres i.(n!)+1 et j.(n!)+1 (pour 1≤i<j≤n)>

L'idée de Goldbach se retrouve en fait dans une démonstration bien plus élémentaire :
Variante de Saidak (2005)
Soit N₁>1. Les entiers N₁ et N₁+1 sont premiers entre eux : leur produit N₂=N₁.(N₁+1) possède donc deux facteurs premiers distincts.
Les entiers N₂ et N₂+1 sont également premiers entre eux.  N₂ possède (au moins) deux facteurs premiers, et N₂+1 en possède un troisième, distinct des deux premiers. L'entier N₃=N₂.(N₂+1) possède donc au moins 3 facteurs premiers. On définit ainsi de suite par récurrence les entiers N_k=N_k-1.(N_k-1+1), et l'entier Nk possède au moins k facteurs premiers distincts.
Il y a donc un nombre infini de nombres premiers.

Démonstration d'Euler (17??)
Euler a évidemment laissé sa trace dans les démonstrations de l'infinité des nombres premiers...

Soit p et q deux nombres premiers. Les sommes des séries géométriques de raison 1/p et 1/q donnent :

En multipliant les deux égalités, on trouve alors que :

A gauche, on trouve donc la somme de tous les entiers de la forme p^α.q^β. On peut généraliser le processus en prenant tous les nombres premiers (la somme de gauche donnera tous les produits de nombres premiers imaginables, le produit à droite est effectué sur l'ensemble des nombres premiers):

Sauf que, d'après le théorème fondamental de l'arithmétique, chaque entier peut s'écrire que d'une unique manière comme produit de nombres premiers (à l'ordre près). La somme de gauche est en fait une somme sur la totalité des entiers :

On reconnaît à gauche la série harmonique, égale à +∞. S'il n'y avait qu'un nombre fini de nombres premiers, le produit de droite serait fini, ce qui est absurde.
Il y a donc un nombre infini de nombres premiers.

Démonstration de Perott (1881)
Au lieu d'utiliser la divergence de la série harmonique, on peut utiliser la convergence de la série des inverse des carrés, avec cette formule, démontrée par Euler :

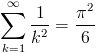
Cette formule est l'œuvre de Euler, mais on peut se contenter pour cette démonstration que cette somme infinie est plus petite que 2 (ce qui se voit en écrivant que , puis en télescopant l'affaire). Bref.

Supposons qu'il existe un nombre fini de nombres premiers :  p₁< p₂< ...< p_r. Soit N un entier plus grand que le produit p₁....p_r.
Le nombre d'entiers inférieurs à N et sans facteurs carrés est 2^r (autant que de sous-ensembles des r nombres premiers)
Le nombre d'entiers inférieurs à N et divisibles par p_i² est au plus N/p_i², donc le nombre d'entiers inférieurs à N et possédant un facteur carré est au plus . Bref, on a donc :

Première inégalité : On partage les entiers entre ceux sans facteurs carrés et ceux avec
Deuxième inégalité : On majore la somme sur les premiers au carré par la somme sur tous les entiers
Troisième inégalité : d'après ce que l'on a dit au début, la série est plus petite que 2 : il existe δ>0 tel que

Maintenant, il suffit de prendre N suffisamment grand (N> 2^r/(δ-1)) pour arriver à la contradiction :
Il y a donc un nombre infini de nombres premiers.

Démonstration de Fürstenberg (1955)
Une petite dernière, la plus récente, qui a la particularité de sortir de nulle part, puisque c'est une preuve topologique ! Pour les allergiques à la topo, cette démo est évidemment pire que celle de Perott...

On définit une topologie sur ℤ en prenant pour base d'ouverts les suites arithmétiques. (Les ouverts seront donc des unions d'ensembles de la forme S_a,b={a+kb|k∈ℤ}). C'est bien une topologie, puisque ces ouverts sont stables par unions quelconques (par définition) et par intersection finies (l'intersection de deux suites arithmétique est soit vide, soit une suite arithmétique où la raison est le ppcm des raisons).
Deux remarques sur cette topologie :
- Un ouvert (non vide) est forcément infini (il contient une suite arithmétique)
- Les ouverts sont aussi fermés (puisque S_a,b=ℤ\(S_a+1,b ∪ S_a+2,b ∪ ... ∪ S_a+b-1,b}

Maintenant, on peut remarquer que n'importe quel entier (sauf -1 et 1) est dans une suite de la forme S_0,p, où p est premier. Autrement dit, ℤ\{-1,1}=∪S_0,p (l'union est faite sur les nombres premiers).
Par les remarques plus haut, l'ensemble {-1,1} n'est pas ouvert (car non infini), donc l'ensemble ℤ\{-1,1} n'est pas fermé. Si l'ensemble des nombres premiers était finie, l'ensemble ℤ\{-1,1} = ∪S_0,p serait une union d'un nombre fini de fermés, et donc, fermé... Contradiction !
Il y a donc un nombre infini de nombres premiers.

Bref, peu importe le chemin que l'on choisi (arithmétique, analyse, topologie...), il y a bien un nombre infini de nombres premiers !

---

Sources :
Paulo Ribenboim - Nombres premiers : mystères et records

Comments

[invité8]

Bonjour,



En fait la formule qui donne la quantité exacte de fois que la conjecture forte est réalisée pour un Pair, par des premiers de forme 6.k ± 1, s'écrit QCok = QGP + QPP + Q2C - NLig dans laquelle :

- QGP + QPP = QPrem = Quantité de Premiers < Pair

- NLig = (Pair - 6) / 6 = Quantité de lignes du tableau des sommes Petit Impair + Grand Impair = Pair, avec Petit Impair de forme 6.k ± 1 et Grand Impair = Pair - Petit Impair,

- et Q2C = Quantité de lignes contenant des sommes du type Petit Composé + Grand Composé = Pair

et qui s'écrit donc aussi QCok = QPrem + Q2C - (Pair - 6) / 6



Pour en savoir plus sur la démonstration de cette formule vous pouvez télécharger ici : http://codes-sources.commentcamarche.net/source/101870-demonstration-de-la-conjecture-forte-de-goldbach-euler

... les fichiers :

- Goldbach_Euler_Résumé_Démo_Tableaux_GG.pdf

- Goldbach_Euler_Démo_Tableaux_GG.pdf



A+.

[yop]

Juste une question concernant la preuve de Perott, il me semble que N est tout le temps plus grand que 2^r(delta -1) vu que delta - 1 est négatif. Voili voulou

[El Jj]

ac > Effectivement, il y a quelques coquilles dans cette preuve. J'espère avoir tout réparé.
Pour ce qui est de la preuve de Furstenberg, j'ai précisé pour le pinaillage. Et puis, c'est vrai que l'union peut être quelconque, mais il n'y a de toutes façons qu'un nombre dénombrable d'ouverts !

[ac]

C'est un peu du pinaillage mais dans la preuve de Furstenberg:
- Un ouvert est forcément infini (il contient une suite arithmétique)

Il faut quand même que l'ouvert soit non vide.

[ac]

Deux petites remarques rapides.
1°) Il y a un ou deux cafouillages dans la démonstration de Perott
a) Ligne 5 entre parenthèses la minoration des séries, dans la seconde il y a des "n" au lieu des "k".
b) Tu commences en disant que la somme des inverses des carrés est inférieure à 2 puis tu fais ensuite comme si elle était inférieure à 1. Ou alors je n'ai rien compris.

2°) Pour la preuve de furstenberg: tu dis que c'est une topologie parce que c'est stable par union dénombrable. dan sune topologie il faut stabilité par union quelconque.