2017+1 (Cette nouvelle année est-elle intéressante ? Episode 09)

Une nouvelle année pointe son nez. Les saisons passent, mais les traditions restent les mêmes. L'année qui arrive sera-t-elle digne d'intérêt, ou parfaitement quelconuque ? Pour le savoir, regardons dans la boule de cristal de l'arithmomancie qu'est l'OEIS, et lisons l'avenir. Rappelons que l'OEIS est l'encyclopédie en ligne des suites entières, qui répertorie toutes les suites d'entiers dignes d'intérêt. Le précepte de base de l'arithmomancie telle que je la pratique annuellement, c'est que plus un nombre est présent dans les suites de cette encyclopédie, plus le nombre sera intéressant.

Les nombres 2015, 2016 et 2017 possèdent respectivement 209, beaucoup trop de et 474 propriétés intéressantes au moment où j'écris cet article. Les années 2015, 2016 et 2017 étaient, vous l'avez probablement remarqué, respectivement assez, incroyablement et très intéressantes ! Et 2018 ?... L'oracle a parlé, cette année sera...

Un peu intéressante !

L'OEIS, unique méthode reconnue par les autorités qui permet de quantifier le niveau d'intérêt d'une année

L'OEIS recense donc 121 propriétés, ce qui n'est pas incroyable, mais respectable pour un nombre qui n'est pas premier, puisque 2018 = 2 × 1009. On est à un niveau comparable à 2014, qui en avait 122. Qu'est ce qui rend le nombre 2018 unique ? Explorons quelques-unes de ses propriétés !

[A191094] : Nombre d'hyperpentacubes fixes sans boucle
Parce que, oui, il y a 121 propriétés, mais aucune n'est vraiment très simple en fait. Il y a très précisément 2018 hyperpentacubes fixes sans boucle. Prenons les mots dans l'ordre.
Un pentacube, c'est un polycube à 5 cubes, c'est à dire un assemblage formé de 5 cubes collés face à face. Dans un espace tridimensionnel classique, il y en a précisément 29 différents :

29 pentacubes :
en bleu, les 6 paires de pentacubes chiraux
en vert, les 5 pentacubes achiraux
en rouge, les 6 pentaminos chiraux solides
en orange, les 6 pentaminos achiraux solides

Enfin, dire qu'il y en a 29 dépend du nombre de façons de les compter. On peut, comme présenté au dessus, compter deux fois les pentacubes différents de leur image dans un miroir (ceux en en bleu), ce qui en donne bien 29. Si on compte ces paires comme indiscernables, il n'y en a plus que 23.

Mais il y a une autre façon de les compter, si on ne prend en compte ni les symétries, ni les rotations. Par exemple, le pentacube « L » peut prendre jusqu'à 24 positions différentes :

Les 24 orientations du pentacube L

En prenant en compte toutes les orientations possibles de tous les pentacubes (on parlera de pentacubes « fixes »), cela nous en donne tout de même un total de 534.

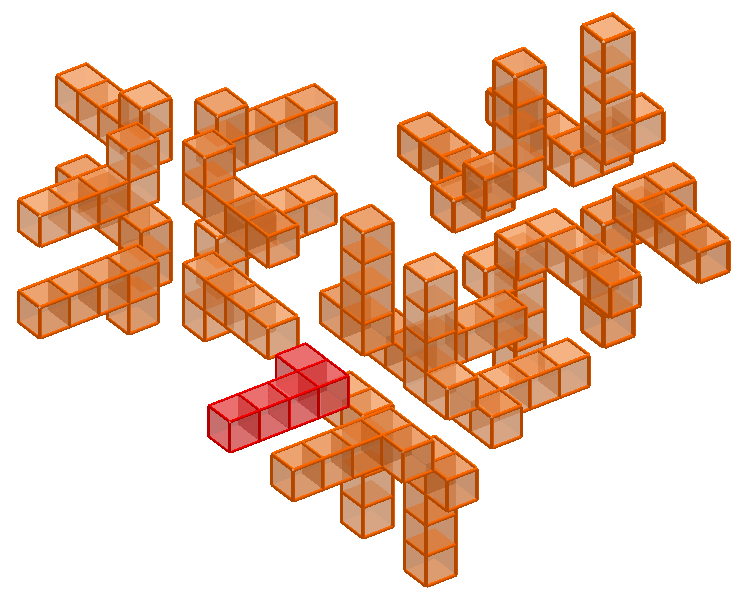
Mais tout ça, ce sont des pentacubes en 3 dimensions. On peut faire le même catalogue pour les pentacubes fixes en 4 dimensions, ce qui augmente un peu le nombre de pentacubes, mais considérablement celui des pentacubes fixes. En effet, la quatrième dimension ajoute de nouvelles orientations à nos pentacubes. À titre d'exemple, le pentacube « L » voit son nombre de positions doubler. Au final, on en obtient au total 2162. Si on retire ceux qui possèdent des boucles (4 cubes collés 2 à 2), on en obtient... 2018 !

Quelques hyperpentacubes non tridimentionnels. La 4eme dimension est représentée par la taille des cubes.

[A229915] : Nombre d'espaliers icosacubiques
Continuons de jouer avec les cubes, et parlons cette fois-ci de polycubes pyramidaux. Il est toujours question de polycubes, c'est-à-dire d'assemblages formés de cubes collés face contre face, mais on va regarder ceux formés de 20 cubes (les icosacubes), et qui sont pyramidaux.
On dit qu'un polycube est pyramidal si il est constitué de rangées successives de plateaux horizontaux, un plateau étant un rectangle plein formés de polycubes, et chaque plateau doit être posé sur un plateau identique ou plus petit :

 
Quelques polycubes pyramidaux formés de 20 cubes
Le premier, en bleu, est constitué d'un plateau 3×4, d'un 2×2 et de deux 2×1
Le deuxième, en rouge, constitué  d'un plateau 4×4 et d'un 2×2
Le troisième, en vert, constitué d'un plateau 2×4, d'un 2×3, d'un 2×2 et d'un 1×2

De tous les polycubes pyramidaux, on en distingue une catégorie particulière, les « espaliers » (bien que je ne voie pas le lien avec les arbres taillés en arbres généalogiques). Ce sont les pyramides dont tous les plateaux sont alignés dans un des coins du plateau de la base (disons le coin nord). Des espaliers à 20 cubes, il en existe très précisément 2018.

 
Quelques polycubes en espalier formés de 20 cubes, parmi les 2018 existant.
Le premier, en bleu, l'unique espalier constitué d'un plateau 3×4, d'un 2×2 et de deux 2×1
Le deuxième, en rouge, l'unique espalier constitué d'un plateau 4×4 et d'un 2×2
Le troisième, en vert, l'unique espalier constitué d'un plateau 2×4, d'un 2×3, d'un 2×2 et d'un 1×2

[A087854] [A056283] : nombre de colliers tricolores à 9 perles
Combien de colliers tricolores à 9 perles peut-on fabriquer avec des perles rouges, jaunes et oranges ? Bien sûr, chaque couleur doit être présente, et deux colliers sont équivalents si on peut obtenir l'un par la rotation d'un autre. La réponse est bien évidemment : 2018 !

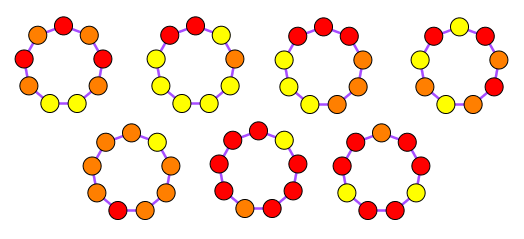
Quelques colliers parmi les 2018 qui existent.

Comment obtenir ce résultat ? C'est l'occasion de ressortir ce bon vieux lemme de Burnside ! D'après celui-ci, le nombre de colliers au plus tricolores à 9 perles différents se calcule en prenant la moyenne du nombre total de colliers fixés par les 9 rotations du collier. En l'occurence, il y a

• 3 colliers (les colliers unicolores) fixés par les rotations de 1/9, 2/9, 4/9, 5/9, 7/9 et 8/9 de tours ;
• 3³=27 colliers (en fixant la couleur de 3 perles successives) fixés par les rotations de 3/9 et 6/9 de tours, comme dans l'exemple ci-contre ;
• 3⁹ (tous, en fait) fixés par l'identité (rotation de 9/9 de tour)

Le nombre de colliers au plus tricolores est donc égal à (3+3+3³+3+3+3³+3+3+3⁹)/9 = 2195.

Il faut alors leur retirer les colliers au plus bicolores, ce qui se calcule de la même façon. Il y a en effet (2+2+2³+2+2+2³+2+2+2⁹)/9 = 60 colliers au plus bicolores. Plus précisément, il y en a 60 jaunes-oranges, 60 jaunes-rouges et 60 oranges-rouges. En n'oubliant pas de retirer les 3 colliers unicolores comptés deux fois, il y a donc 3 × 60 - 3 = 177 colliers au plus bicolores différents.

Le nombre de colliers différents exactement tricolores est donc 2195 - 177 = 2018. CQFD.

Et sinon...

• Il y a 2018 façons d'écrire 60 sous la forme d'une somme décroissante de nombres premiers (comme 60=19+11+11+7+7+5) [A000607]
• Il y a 2018 termes non nuls dans le développement de (x-y)(x²-y²)(x³-y³)...(x⁶⁶-y⁶⁶) [A086781]
• Il existe 2018 graphes à 9 noeuds qui possèdent un cycle eulérien [A133736]

 Et la santé !

Comments

[Grob]

Pourquoi j'en trouve 321 ? :O