Brenoms de nom

Où en étions-nous, déjà ? J'ai parlé des entiers naturels, des relatifs, des rationnels... Ah oui : les réels... Tout le monde s'attend donc aujourd'hui à ce que je parle des complexes, et c'est pourquoi je ne le ferai pas... Aujourd'hui, place aux brenoms !

L'anneau des 10-adiques
Jusqu'à maintenant, les nombres, dans leur grande majorité, possèdent une infinité de chiffres après la virgule.
Et si on s'autorisait maintenant à mettre une infinité de chiffres avant la virgule ? Par exemple, ...172172172. N'y cherchons pas trop de sens, c'est pour l'instant qu'une théorie... Ces nombres portent le doux nom de "brenom", de "nombres décadique" ou de "nombres 10-adique"

Et si on additionnait ces nombres ?
Les décadiques s'additionnent comme de simple entiers : on pose l'addition, et on effectue les retenues quand il le faut vraiment.

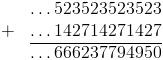
Pour la multiplication, c'est pareil : on la pose, on effectue toutes les retenues nécessaires, et on trouve le résultat. C'est évidemment un peu plus compliqué, mais ça se fait :

Le produit, comme la somme, se comportent bien : pour connaître les n derniers chiffres de a+b ou de a×b, il suffit de connaître les n derniers chiffres de a et de b.

Mais le report de la retenue peut entraîner des surprises, notamment :

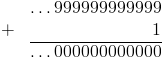
Avec les réels et leur nombre infini de chiffres après la virgule, nous n'avions aucun problème existentiel : les chiffres qui apparaissent loin dans le développement décimal n'ont pas vraiment de poids. Pour les 10-adiques, c'est l'inverse : les très grands nombres, comme 10ⁿ, n'ont pas beaucoup de poids, seuls les plus à droite sont importants. Avec le report à l'infini de la retenu, le résultat de cette somme est bien 0.(De la même façon que 0.999... = 1).

Autrement dit, ...99999 + 1 = 0 !
Vu d'une autre façon, on a ...999999 = -1.

Avec les décadiques, plus besoin des nombres négatifs ! Pour le calcul d'un opposé d'un décadique n quelconque, il suffit simplement de chercher quel nombre il faut ajouter pour obtenir ...9999999, et d'y ajouter un. On trouve par exemple que -...523523523 = ...476476477 :

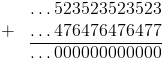
On peut y faire des additions, des multiplications et même calculer des opposés (et donc faire des soustractions) : l'ensemble des décadiques, noté ℤ₁₀, est un anneau !

L'anneau non intègre des 10-adiques

Et pour la division ?
De manière générale, diviser a par b, c'est multiplier a par l'inverse de b. Pour diviser tout par n'importe quoi, il faut donc savoir inverser n'importe quoi.
Pour les décadiques, trouver l'inverse de a, c'est trouver le nombre b tel que a×b = ...00001.
Certains cas se révèlent plus faciles que d'autres, notamment l'inverse de 3 :

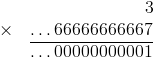
Et donc, 1/3 = ...66666667 = 0.3333333...
Moralité : plus besoin des nombres à (une infinité de) virgules !
Pour diviser n'importe quel nombre par 3, il suffira donc de multiplier par ...6666666667.

D'autres cas se révèlent impossibles : comment trouver l'inverse de 5 ? Il faut donc trouver un nombre a entre 0 et 9 tel 5×a se termine par un 1... impossible ! Idem pour 2.
Pourtant, l'inverse de 5 se trouve facilement dans ℚ, et c'est 0.2.
Finalement, pour avoir un ensemble de nombre à peu près cohérent, il semble nécessaire de permettre un nombre fini de chiffres après la virgule. On obtient alors les nombres décadiques à virgule, notés ℚ₁₀.

Dans ℚ₁₀, on peut donc facilement diviser par 3, par 2, par 5... Plus généralement, on peut facilement diviser par n'importe quel entier n (∈ℕ), en s'intéressant aux diviseurs de n.
Si n n'est divisible ni par 2, ni par 5 (n termine par 1, 3, 7 ou 9), alors 1/n possèdera un développement décimal infini et périodique : 1/n = 0,(v) (où v est une séquence de décimales qui se répète).
Alors, dans ℤ₁₀, l'inverse de n sera le décadique (v')U (où v' est le complémentaire de v pour arriver à 9...9, et U=v'+1).

Par exemple, quel est l'inverse de 231 dans  ℚ₁₀ ? Il suffit de commencer par calculer 1/231 :

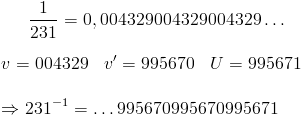
Si n est divisible par 2 ou 5, alors n=5×n' ou n=2×n'. Il ne reste plus qu'à trouver l'inverse de n', l'inverse de n sera donc 1/n'×0.2 ou 1/n'×0.5.

Bref : les entiers naturels (et donc les entiers relatifs vu comme des décadiques) sont inversibles dans ℚ₁₀. De manière encore plus générale, tout décadique dont la dernière décimale est 1, 3, 7 ou 9 est inversible dans ℚ₁₀.

Mais pour ce qui est des décadiques de manière générale, les choses ne sont pas aussi simples : certains nombres ne sont pas inversibles, qu'on le veuille ou non.
Imaginons que l'on puisse trouver deux nombres (non nuls) a et b tels que a×b=0 (*). Si a possède un inverse a^-1 (et donc a^-1×a=1), et en multipliant par a^-1 dans (*), on trouve b=0 : c'est impossible ! Si on trouve donc deux éléments a et b tels que a×b=0, alors on aura sous la main deux nombres ne pouvant pas posséder d'inverse.

Deux tels nombres s'appellent "des diviseurs de 0", et on peut en trouver dans  ℚ₁₀ (sinon, j'en aurais pas fait tout un paragraphe). Ils ne se laissent pas facilement attraper (ils ne peuvent pas être périodiques, notamment). Par exemple, on a :

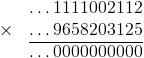
Bref : l'ensemble des 10-adiques est chouette, mais on ne peut pas diviser tout par n'importe quoi, ce qui est bien dommage...

Le corps des p-adiques

Ce qui a essentiellement posé problème, ce sont les nombres terminant par 0, 2, 4, 5, 6 ou 8, autrement dit, les nombres qui ne sont pas premiers avec 10. Pour oublier ce problème, un seul remède : passer de la base 10 à la base p.

Rappelons-le tout de même : quand on écrit le nombre 3841, on écrit en fait :

Mais on a aussi :

Dans la base 7, le nombre s'écrit 14125. On écrit alors 3841₁₀=14125₇.

Même si l'on changeant la base d'écriture des nombres, les règles pour poser une addition ou une multiplication restent toujours les mêmes. La définition des 10-adiques peut donc être transposée dans n'importe quel base, et seront alors appelés "nombres p-adiques". On distingue toujours les entiers p-adiques, notés ℤ_p, et les p-adiques (à virgule), notés ℚ_p.

Petit exemple d'addition dans ℤ₇ :

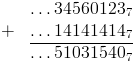
Lorsque l'on fait de bêtes calculs dans ℕ, la base dans laquelle on travaille n'intervient pas. Pour les p-adiques, les choses sont différentes ! Les bases les plus intéressantes sont les bases premières : si p est premier, tout nombre de ℚ_p sera inversible !

Bref : pour p premier, ℚ_p est un corps (on peut diviser tout par n'importe quoi (sauf par 0)), au même titre que ℚ ou ℝ.

En plus d'être un corps, ℚ_p partage une autre propriété avec ℝ : ce sont des corps complets, qui ne possèdent pas de trous comme dans ℚ.
Plus précisément, pour dire qu'un ensemble est complet, il faut définir une distance. Pour définir la distance entre deux p-adiques a et b, on s'intéresse au nombre a-b.
Si a-b=0, on pose d(a,b)=0
Sinon, on pose d(a,b)=p^-c(a-b), où c(n) compte le nombre de 0 à la fin de l'écriture de n.

Cette définition de la distance permet de légitimer le fait de dire que 10ⁿ est d'autant plus proche de 0 que n est grand (et donc ...666666₇ + 1₇ = 0₇ ).

On peut alors démontrer que les suites de Cauchy de ℚ_p (les suites qui se resserrent autour d'une valeur limite) convergent toujours vers un nombre de ℚ_p : l'ensemble n'a pas de trous, il est complet.

Plus fort encore : l'ensemble ℚ_p, contrairement à ℝ, est compact !
Un espace métrique E (un endroit où une distance a été définie) est dit compact si, pour toute suite u_n (infinie) de E, on peut y extraire une sous-suite (une sélection de termes dans u_n) qui converge dans E.
L'ensemble ℝ, par exemple, n'est pas compact : on ne peut trouver dans la suite (0,1,2,3,4,5,...) une sous-suite qui convergera.
Dans ℚ_p, la donne est différente : de la suite (0,1,2,3,4,...), on peut notamment extraire la sous-suite (1,10,100,1000,...), qui converge vers 0 dans ℚ_p.

La construction intuitive des p-adiques (des nombres infinis à gauche) peut se formaliser de la même façon que la construction intuitive des réels (des nombres infinis à droite). Alors que l'ensemble ℝ résulte de classes d'équivalence de suites de Cauchy de ℚ, l'ensemble ℚ_p résulte quant à lui de classes d'équivalence de suites de Cauchy sur ℚ, mais en prenant une autre définition de la distance, dite norme p-adique (Les suites de Cauchy ne seront donc pas les mêmes).

Bref : ℚ_p, c'est comme ℝ, mais en mieux !

Les nombres p-adiques sont les jouets principaux des mathématiciens d'aujourd'hui : on essaye de faire sur ℚ_p tout ce que l'on sait déjà faire les yeux fermés sur ℝ (définir des fonctions et les dériver sans vergogne, résoudre des équations différentielles). Et quand on y arrive, on essaye de faire encore mieux : découvrir des propriétés sur ℚ_p pour les ramener sur les réels.
On a même trouvé des applications des p-adiques à l'informatique ou à la physique...

---

Sources :
Les nombres p-adiques, par Yann Ollivier (beaucoup de questions, mais sans les réponses)
Nombres décadiques ou brenoms, par Alain Pichereau (encore plus de questions, mais avec leur réponse)

---

Autres articles de cette série : ℕ,  ℤ, ℚ, ℝ, ℚ_p, ℂ (1), ℂ (2), H, 𝕆, ℚ(α), 𝔽_q, No

Comments

[Spencer]

Je me souviens d'un collègue de boulot sympa qui rêvait pour sa retraite de faire des maths sur un grand tableau noir posé en pleine nature, face à la montagne enneigée. Un genre de poésie un peu surréaliste qu'on retrouve dans cet article.
Kenavo

[Ni©las]

Hello Jj,

Je trouve ce sujet très intéressant, peux-tu me dire si on le croise en Master 1 MFA à Nantes ?

++

[Paul]

Il ne s'agit pas des « brénoms », mais des « brenoms » (« nombres » à l'envers).