C'est pas encore fini ?

Résumé des épisodes précédents :
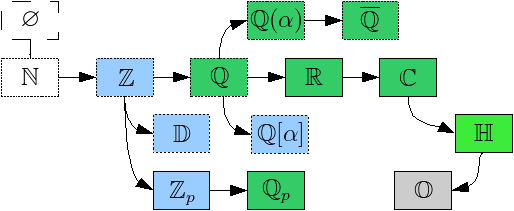
bla bla... corps des complexes... bla bla... polynôme irréductible... bla bla... nombre algébrique... bla bla... nombres algébriques... bla bla... extension de corps... bla bla... passage au quotient... bla bla bla...corps de rupture... bla bla... Complétons ce diagramme !

Ce qu'est un nombre, les mathématiciens ne le savent pas vraiment, mais cela n'empêche pas de travailler avec ! Pour la dixième fois consécutive, découvrons aujourd'hui de nouveaux nombres, avec ces nombres qui font le plaisir de tous les arithméticiens : les corps finis !

Les groupes cycliques
Calculs modulo 24
(Où je donne un premier exemple de calcul dans un groupe cyclique)
Il est 19h. Quelle heure sera-t-il 28 jours heures plus tard ?
28 heures, c'est 24+4 heures. Puisque 24 heures représentent un jour, on les oublie et on ne garde que les 4 heures restantes pour le calcul. Dans 28 heures, il sera donc 23 heures !
En supposant implicitement que 24=0, on s'autorise finalement à dire que 19+28=23 !

Faire des calculs modulo 24 revient en fait à faire les calculs comme on a l'habitude de les faire (dans ℤ), puis d'en prendre le reste en faisant la division euclidienne par 24.
Par exemple, 19+28 = 47.
La division euclidienne de 47 par 24 donne 47 = 24×1 + 23. Le reste est donc 23.
On se permet alors de dire 47 = 23.

Calculs modulo 60
(Où je pars dans un délire philosophico-mathématique sur le sens de l'addition)
Changeons d'exemple, et intéressons-nous maintenant seulement aux minutes. Il est **h30. Quelle heure sera-t-il dans 80 minutes ?
En procédant aux mêmes calculs, cette fois-ci modulo 60, on s'aperçoit que 80=60+20. En admettant  que 60=0 on a 80=20. Le calcul donne 30 + 80 = 30 + 20 = 50. Dans 80 minutes, il donc sera **h50.
Dans la pratique, on ne dira jamais qu'il est "** heures 50", mais on dira plutôt qu'il est "** heures moins 10".  Un problème d'unicité se pose !

L'ensemble dans lequel on décide que 60=0 s'appelle ℤ/60ℤ. Dans cet ensemble, on a l'égalité -10=50, ce qui pose quelques problèmes pour nommer les nombres qui y habitent.

Il y a alors deux façons (équivalentes) de concevoir l'ensemble ℤ/60ℤ :
- La première consiste à dire que ℤ/60ℤ = {0,1,2,3,...,59}, et de définir pour chaque couple de nombre leur somme. On va par exemple dire que 51+14=5. Le calcul 30+80 n'a donc aucun sens, puisque le nombre 80 n'existe même pas !
- La seconde manière de voir les choses est de prendre la définition exacte de ℤ/60ℤ : le nombre que l'on appellera entre autres manières 0 sera l'ensemble {...,-120,-60,0,60,120,..}, noté aussi 0+60ℤ ou plus simplement 0 (On dit que cette ensemble est une classe d'équivalence, et le nombre 0 en est un représentant). Le nombre que l'on peut appeler 14 sera l'ensemble {...,-46,14,74,...}, noté 14+60ℤ.
L'addition + que l'on définit sur ℤ/60ℤ est alors définie sur les classes d'équivalences, et non sur les représentants de ces classes (Le petit trait au-dessus n'est là que pour distinguer l'addition dans ℤ/60ℤ de celle sur ℤ). On a, par exemple, (51+60ℤ) +  (14+60ℤ) = (5+60ℤ).
De là à écrire que 51 + 14 = 5, il n'y a qu'un pas, que l'on franchit sans trop se poser de question. On s'appuie en fait sur un théorème tout à fait extraordinaire :

(a+60ℤ) + (b+60ℤ) = (a+b)+ℤ
que l'on peut écrire également :a + b = a + b

Dans cette égalité, on trouve trois types d'additions a priori différentes, mais qui représentent une même réalité, vue sous différents points de vue :
* le + rouge est une action de groupe, mais c'est surtout ici une commodité d'écriture pour parler des différentes classes d'équivalence : 51 + {...,-60,0,60,...} = {...,-9,51,111,...}
* le + (et le -) vert  est l'addition sur ℤ (sur des nombres entiers relatifs) : 51 + 14 = 65
* le + bleu est l'addition sur ℤ/60ℤ (sur des classes d'équivalences). 51 + 14 = 5

Grâce au théorème, l'addition verte et l'addition bleue se correspondent. Par la suite, elle redeviendra l'addition noire, et je confondrais volontairement les entiers de ℤ et les représentants de classes d'équivalence dans ℤ/nℤ.

Dans tous les cas, l'ensemble   ℤ/nℤ possède exactement n éléments (les classes des nombres entre 0 et n-1). C'est donc un groupe (parce qu'on peut y faire additions et soustractions) fini (un nombre fini d'éléments).

Calculs modulo 10
(Où on va découvrir que la multiplication pose quelques problèmes)
En fait, les deux premiers exemples sont de très mauvais exemples, puisqu'ils illustrent d'une très mauvaise manière la notion de groupe : bien que 0h+0h a un sens, le calcul minuit+minuit ne veut absolument rien dire ! (C'est plutôt une illustration de la notion d'action de groupe, mais le propos n'est pas là...)

Faute de meilleur exemple, revenons dans le domaine mathématique. Prenons par exemple ℤ/10ℤ, que l'on utilise quand on se fait la remarque "Le calcul 1764+74088=156457 est manifestement faux, les unités ne concordent pas". Faire des calculs dans ℤ/10ℤ, c'est s'intéresser seulement aux unités dans les calculs que l'on fait.

Ce qu'on a fait dans ℤ/60ℤ marche très bien pour ℤ/10ℤ : l'addition est parfaitement définie, sans ambiguïtés. Et pour la multiplication ?...

"Puisque 4*8=2, le produit 1764*74088 devrait se terminer par un 2".

Le fait que la multiplication marche bien (ie, qu'elle ne dépende pas du représentant que l'on prend) dans ℤ/nℤ est tout à fait extraordinaire, au moins autant que pour l'addition. (Quand on regarde de plus près, on s'aperçoit que les propriétés de ℤ/nℤ sont en fait héritées de celle de ℤ)

Une addition, une soustraction et une multiplication : tout ce qu'il faut pour faire de ℤ/nℤ un anneau. Seule la division pose problème.

Revenons sur l'exemple de ℤ/10ℤ. Quel est l'inverse de 3 ? Autrement dit, par quoi multiplier 3 pour obtenir 1 ?. Un coup d'œil sur la table de multiplication permet de répondre à la question : 3×7 = 1. On a donc 3^-1 = 7.

Toujours dans ℤ/10ℤ, quel est l'inverse de 5, ie, par quoi multiplier 5 pour obtenir 1 ? Quand on regarde la table de multiplication, on est vite déçu : multiplier 5 par un autre nombre ne peut donner que 0 ou 5, impossible donc d'avoir 1.
Le nombre 5 n'est donc pas inversible dans  ℤ/10ℤ, on peut oublier les divisions par 5...

Finalement, quels sont les nombres inversibles dans ℤ/10ℤ ? On peut en compter 4 : les nombres 1, 3, 7 et 9. Ce sont d'ailleurs les seuls inférieurs à 10 n'ayant pas de diviseurs commun avec 10 (on dit qu'ils sont premiers avec 10). Un raisonnement peut montrer que les inversibles de ℤ/nℤ sont en fait seulement les entiers premiers avec n...

Les corps finis premiers
Mais un nombre, ça doit quand même pouvoir se diviser (Je ne jure que par les corps de nombres)... L'ensemble ℤ/10ℤ n'est à ce titre pas du tout satisfaisant ! Par quoi remplacer 10 pour faire de ℤ/10ℤ un ensemble où tous les nombres seront inversibles ?

On l'a vu juste au-dessus : pour qu'un nombre soit inversible dans ℤ/nℤ, il faut qu'il soit premier avec n. Il faut donc prendre n tel que tous les nombres entre 1 et n-1 soient premiers avec lui. De tels nombres sont appelés nombres premiers : ce sont les nombres admettant exactement deux diviseurs !
Les premiers exemples sont 2, 3, 5, 7 et 11, soit tout autant de corps finis !

Tables de multiplication dans ℤ/2ℤ, ℤ/3ℤ, ℤ/5ℤ et ℤ/7ℤ

Les corps finis
On a donc pour l'instant toute une classe de corps finis : les corps de la forme ℤ/pℤ, où p est un nombre premier. On peut montrer que n'importe quel corps à p éléments (où p premier) est isomorphe à ℤ/pℤ (autrement dit, si on possède un ensemble à p éléments où une addition et une multiplication ont été définies, alors ils auront la même table d'addition et de multiplication que ℤ/pℤ).

On a donc tendance à noter 𝔽_p, plutôt que ℤ/pℤ, pour parler du corps (field) de cardinal p (ie, à p éléments).

Seulement des corps finis avec un cardinal premier ? On a vite fait le tour... Existe-t-il des corps ayant un cardinal non premier ? Si oui, à quoi ressemblent-ils ? Et peut-on trouver des corps finis de n'importe quel cardinal ?

Premier point : si deux corps possèdent le même cardinal, ils sont isomorphes (même table d'addition/de multiplication, à un renommage près). Si on trouve un corps à q éléments (q non forcément premier), on pourra donc l'appeler 𝔽_q, sans ambiguïtés.

Deuxième point : un corps de cardinal non premier, ça existe ! La preuve avec celui-ci, que je vais logiquement appeler 𝔽₈.

Table d'addition et de multiplication de 𝔽₈.

En fait, tous les  𝔽_q n'existent pas (il n'existe pas de corps de cardinal 10, par exemple). Un corps fini ne peut avoir qu'un cardinal de la forme q=pⁿ, avec p premier et n≥1.

Construction de 𝔽_q
Si vous avez aimé la construction des extensions du corps ℚ (là-bas), vous allez adorer la construction de  𝔽_q ! Si vous n'êtes pas dans ce cas, ça risque d'être moins intéressant...

Idéalement, la construction d'un corps fini comme 𝔽₈ se construirait de la même façon que ℚ(√2) : on part d'un corps premier (ℚ pour ℚ(√2), 𝔽₂ pour  𝔽₈) et on lui ajoute de nouveaux éléments. Pour ℚ(√2), on le fait sans trop de problèmes, puisque l'on peut voir ℚ(√2) comme un sous-ensemble de ℝ, que l'on connaît bien. Pour 𝔽₈, on ne peut pas faire la même construction, puisque l'on ne peut pas voir   𝔽₈ comme sous-ensemble de quelque chose de plus grand. Il faut donc passer par la version abstraite des choses, et passer par les polynômes...

Pour ℚ(√2), on a utilisé le polynôme X²-2, et on a construit l'ensemble ℚ[X]/(X²-2), pour fabriquer artificiellement des racines à X²-2 dans ℚ (et on a obtenu quelque chose de dimension 2 sur ℚ).

Pour 𝔽₈, on va suivre le même processus. Prenons un polynôme à coefficients dans  𝔽₂ (coefficients 0 ou 1). Disons P(X)=X³+X+1. Ce polynôme ne possède pas de racines dans 𝔽₂  (P(0)=1 et P(1)=1), et est irréductible (impossible de l'écrire sous la forme P(X)=(X²+bX+c)(X+d)). On va donc artificiellement lui ajouter des racines, en considérant l'ensemble 𝔽₂[X]/(X³+X+1).

Cet ensemble est composé des polynômes à coefficients dans 𝔽₂ et de degré inférieur à 3. On peut le dire autrement : cet ensemble possède 8 éléments :

0, 1, X, X+1, X², X²+1, X²+X, X²+X+1

Et en plus, l'élément X vérifie la relation X³+X+1=0 (ou X³=X+1). A partir de ces quelques informations, on peut recréer la table d'addition et de multiplication :

Table de multiplication des éléments de 𝔽₂[X]/(X³+X+1).

Comme par hasard, ce tableau est exactement le même que celui de 𝔽₈ un peu plus haut !

Pour construire un corps fini 𝔽_q, avec q=pⁿ, il suffit en fait de construire l'ensemble 𝔽_p[X]/(P), où P est un polynôme irréductible de degré n.

Le corps 𝔽₂₅₆ peut se construire notamment à partir du polynôme M(X)=X⁸+X⁴+X³+X+1. Dans la réalité, ce corps est utilisé pour crypter les communications du gouvernement américain, puisqu'on le retrouve dans l'algorithme de cryptographie Rijndael.
Pourquoi ce polynôme et non pas l'un des 29 autres qui aurait aussi bien fait l'affaire ? Tout simplement parce que c'est ce polynôme qui permet de minimiser la complexité des calculs ! (Comme pour le corps des complexes : on peut y faire des calculs simples en utilisant la base (1,i), mais on pourrait aussi utiliser la base (1, (-1+i√19)/2)...)

En tout cas, je peux ajouter de nouvelles cases à mon chouette diagramme des nombres !

(J'ajoute au passage deux autres cases pas très intéressante : 𝔽_q, la clôture algébrique de 𝔽_q, et ℤ[α], les entiers quadratiques)

Et la prochaine fois, j'espère peut-être terminer cette trop longue série, en répondant à cette question : qu'est ce qu'un nombre ?

---

Sources :
N'importe quel bon bouquin d'algèbre...

---

Autres articles de cette série : ℕ,  ℤ, ℚ, ℝ, ℚ_p, ℂ (1), ℂ (2), H, 𝕆, ℚ(α), 𝔽_q, No

Comments

[Robyn Slinger]

Ah, on me donne souvent cette réponse qui est, bien entendu, techniquement correcte. Mais pourtant, il existe bien un objet mathématique qu'on appelle ainsi et qui est à la mode en ce moment (en fait il existe plusieurs théories). Un point de vue est exposé par exemple dans
http://arxiv.org/abs/0911.1989

[El Jj]

Robyn Slinger > Suivant les définitions que l'on prend pour un corps, le corps à un élément peut ou non exister. S'il existe, c'est l'anneau nul {0}, et il ne sert à rien...

Remy > Bien vu pour la faute dans la table de multiplication ! J'espère que c'est la seule faute qui reste ! J'ai pris en compte les deux autres erreurs de formes.

Pour la phrase "l'élément X vérifie la relation X^3+X+1=0 (ou X^3=X+1)", Robyn Slinger a répondu plus vite que moi : le passage au quotient force la relation X^3+X+1=0, et le corps F_2 donne -1=1.

La théorie de Galois n'était pas au programme de cette saga, mais pourquoi pas ?!

[Robyn Slinger]

"J’avoue que je ne comprends pas la phrase apparemment évidente pour tout le monde sauf pour moi : « Et en plus, l'élément X vérifie la relation X3+X+1=0 (ou X3=X+1). » Pourriez-vous me donner quelques explications supplémentaires pour éclairer mes faiblesses ?"

Ah, eljj a grillé une étape. L'élément X vérifie effectivement par construction la relation X^3+X+1=0 : quotienter l'anneau de polynômes F_2[X] par (X^3+X+1) revient à imposer la relation "X^3+X+1=0" dans le quotient. Comme quand on regarde l'anneau fini ZZ/24ZZ, cela revient à décréter que désormais, "24=0".

Cela étant, on a donc X^3+X+1=0, soit X^3= -X-1. Or ici on travaille au-dessus de F_2, le corps à deux éléments, autrement dit ZZ/2ZZ. Et dans F_2, on voit que -1=+1 (parce que 2=0), donc -X-1 = X+1 et il vient X^3=X+1.

C'est plus clair comme ça ?

[Rémy]

Bonjour,
N’y aurait-il pas une erreur dans la table de multiplication dans F8 : a x c = b et non d ?
De même, concernant la table de multiplication dans F2[X]/(X3+X+1) : X x X² = X + 1 et non X² + 1 ?

J’avoue que je ne comprends pas la phrase apparemment évidente pour tout le monde sauf pour moi : « Et en plus, l'élément X vérifie la relation X3+X+1=0 (ou X3=X+1). » Pourriez-vous me donner quelques explications supplémentaires pour éclairer mes faiblesses ?

Quelques remarques pour améliorer l’article sur la forme :
Juste après l’image des tables d’addition et de multiplication dans ℤ/10ℤ, la phrase : « Le fait que la multiplication marche bien (ie, qu'elle ne dépende pas du représentant que l'on prend) dans ℤ/nℤ est aussi miraculeuse que l'addition. » n’est pas correcte : c’est le fait qui est miraculeux et la phrase… pas géniale.

Dans le chapitre sur les corps finis premiers, On trouve la phrase : « pour qu'un nombre soit inversible dans ℤ/nℤ, il faut qu'ils soient premier avec n. Il faut donc prendre n tel que tous les nombres entre 1 et n-1 soit premiers avec lui. » On devrait avoir : « pour qu'un nombre soit inversible dans ℤ/nℤ, il faut qu'IL SOIT premier avec n. Il faut donc prendre n tel que tous les nombres entre 1 et n-1 SOIENT premiers avec lui. »

En tout cas, merci pour cette saga et votre style original pour parler mathématique. Je continue à la suivre en espèrant y pêcher quelques éléments qui me permettront de progresser et comprendre enfin un jour peut-être la théorie de Galois.

Rémy

[Robyn Slinger]

Aura-t-on droit à une excursion vers les "corps de caractéristique 1"?